Coordinate Transformation Matrices and Angular Rates

At this point I advise you to review Chapter 3. It will lubricate your understanding of the abbreviated derivations that follow. Besides the transformations, I will also deal with the angular velocity vectors u>BU and u>UI because they can be derived directly from our orange peel diagrams.

9.1.2.1

Transformation matrix of velocity wrt inertial coordinates. The inertial coordinates are defined in Chapter 3. Figure 9.1 turns the world upside down so that the heading and flight-path angles take their conventional orientation, and we can readily switch later to flat-Earth approximation. However, jzщ and вщ are at this point not the usual heading and flight-path angles. They are referenced to the Earth-centered inertial (J2000) coordinate system for the sole purpose of for­mulating Newton’s equations wrt the inertial velocity frame. We call them inertial heading and flight-path angles to distinguish them from the standard heading and flight-path angles, which we will derive later.

The inertial coordinate system ]7 is associated with the inertial frame I. Its axes are defined as follows: l7 is the direction of vernal equinox, and 37 is the Earth rotation axis. The inertial velocity axes ]u are associated with the inertial velocity frame and given by the following: u is the direction of velocity vector, 2U is in l7, 27 plane; фщ is the inertial heading angle; and вщ is the flight-path angle. The standard sequence of transformation is

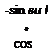It is similar to the transformation sequence in Sec. 3.2.2.6 of the flight-path coordi­nates wrt geographic coordinates. Only here we start with the inertial coordinates ]7 and end up with the velocity coordinates ]L. The transformation matrix is

Let us take the opportunity and derive the angular velocity of the velocity frame wrt the inertial frame. In Fig. 9.1 the angular rates of the inertial heading and flight-path angles are indicated. Combining them with their respective unit vectors and adding them vectorially yields

U)UI = фщІз + вщІІ2 (9.6)

Later we will need their component form in the velocity coordinate system. So let us express the inertial unit vector in its preferred coordinate system ]7 and convert it to the Ju coordinates

[coUIf = фщ[Т]шЦз]! +вщШи

and multiplied out with the help of Eq. (9.5)

Ф UI sin вщ вщ

Ф UI C0S віл

The angular velocity of the inertial velocity frame wrt the inertial frame is a function of angular rates and the flight-path angle but not the heading angle. Both the angular rates and the flight-path angle are obtained by solving the equations of motion.

We now turn to the incidence angle transformation matrices and their angular rates. As already discussed, we must distinguish between the skid-to-tum and the bank-to-turn cases for missiles and aircraft, respectively.