Equations of motion relative to the Earth frame

10.1.2.4 The geo­graphic modeling of the equations of motion over an elliptical Earth focuses on the integration of the geographic acceleration DEvER relative to the Earth rather than the inertial acceleration D’v’B. Make no mistake, the J2000 is still the inertial frame for Newton’s and Euler’s laws. We just introduce the Earth as a convenient reference frame. I will derive the relationship between the two velocities and their accelerations before presenting the translational equations. As before, the attitude equation holds no surprises.

There are two reasons for focusing on the geographic velocity vf: 1) the at­mosphere is rotating with the Earth, and the aerodynamic forces are a function of the geographic velocity; 2) the vehicle’s position and velocity are traced more conveniently over the Earth than in the inertial frame.

By definition, the inertial velocity is v B = D’sbi, where s bi is the location of the vehicle c. m. В wrt the center of the Earth /. To introduce the geographic velocity, we change the reference frame from I to E

D! sbi — DeSbi +

Now, introduce a reference point on the Earth E (any) as an intermediary between В and /:

вві = sbe + sei (10.50)

and substitute it into the preceding equation

D1sbi = Desbe + Desei + Qeisbi

DesEi = 0 because sei is constant in the Earth frame. Using the definition of geographic velocity vB = Desbe, we get the desired relationship between the inertial and geographic velocities:

v’B =vb+^EIsbi (10.51)

The translational differential equation is derived from Newton’s second law

mDlv’B = f a p + mg

It must be modified to bring out the geographic velocity. We first deal with the rotational derivative and transform it to the frame E

D’v’g = DEv’B + nE’v’B (10.52)

then we modify the first term on the right-hand side by substituting Eq. (10.51)

DEv’g=DEvE + DE(nE’sBI)

and subject the last term to the chain rule

De(EIe’sBi) = DEnEIsH, + EIeiDesBi

The first term on the right-hand side is zero because the Earth’s angular velocity is constant. The second term can be expanded:

nEIDEsBi = ftEI(DEsBE + Desei) = CIeiDesBe = ПЕІуЕв

Collecting terms

Dev’b = DEvEB + SlE’vEB

substituting them into Eq. (10.52) yields

D! v!b = Deveb + SlEIvEB + nE! v!B

and finally replacing the last v! B by Eq. (10.51) we get a relationship between the inertial and gravitational accelerations

D‘v’B = Deveb + 2flEIvEB + flEInE! sBI (10.53)

We identify the Coriolis term 2flEIvB and the centrifugal term flEIflEIsBi that we first encountered in Sec. 5.3.1. Replacing the inertial acceleration in Newton’s equation by Eq. (10.53), we obtain the translational equation

DEvE = – f +g – 2SlE, vEB – ПЕ! ПЕІ*ВІ (10.54)

m

It is exclusively a function of the geographic velocity and acceleration, although it governs the translational equations of motion relative to the inertial frame. It is also still in the invariant tensor form and therefore holds in any coordinate system. In particular, if we chose a coordinate system that is associated with the Earth’s reference frame E, the rotational time derivative will turn into the ordinary time derivative. We have three choices; the Earth ]£, the geocentric ]G, or the geodetic ]° coordinate systems. Most likely, we want the geographic velocity computed in geodetic coordinates. In this case we program

^11 = i[f]BD[f f + [Г]ОС[ ]G

at J m

-2[T]d,[£2ei]![T]di[uf]D – [7′]°/[^£/]/[^£/]/[sb/]/ (10.55)

Each term on the right-hand side is expressed in the most suitable coordinate sys­tem: the forces in body coordinates, Earth’s gravitational acceleration in geocentric coordinates, Earth’s angular velocity in inertial coordinates, and the geographic velocity in geodetic coordinates. The vehicle’s displacement is referenced to the center of Earth [.vb/]1 and is shown in inertial coordinates. It could as easily, with the help of Eq. (10.50), be expressed in geodetic Earth-referenced position [sbe]1* (point E can be any reference point fixed in the Earth frame)

[SB/]7 = [T]d,[sbe]D +

The transformation matrices [T]DG and [T]DI have already been given, where [T]BD is obtained from the direction cosine matrix calculations.

An alternate form of Eq. (10.55) is also useful. It stems from the require­ment of calculating the incidence angles a and /8. They are derived from the geographic velocity expressed in body axes [uf]B. We could of course obtain it from [u|]B = [T]BDvf ]°, but some aerospace professionals prefer to formulate the geographic acceleration in body coordinates proper. In that case we take the perspective of the geographic velocity from the vehicle’s body frame and make an Euler transformation to body frame В

Substitution into Eq. (10.54) yields

Dbveb + nBEvEB = – f +g- 2nE! vEB – nE! nE1sBI

m

Expressed in body coordinates the rotational derivative will convert to the ordinary time derivative, and Newton’s equations are programmed as

= -[£2B£]B[uf ]B + -[fa, p]B + [T]BG[gf L J m

– 2[rf[n0];[f ]BI[vEB]B – [Г]в/([^£/]/[^£/]/[^/]/) (10.56)

where [QBE]B = [^й/]й – [Т]Ш[ПЕІУ[Т]В!, [QBI]B is obtained from Euler’s equation, and [T]BI from the direction cosine equation. Equation (10.56) is also found in this form in the book by Stevens and Lewis [Eqs. (1.3-1.6)].9

Having obtained the geographic velocity vf defined as vf = Desbi from inte­grating Newton’s equation, a second differential equation solves for the inertial position sB1:

D! sBi = DesB! + flEIsBI

Note that the inertial point I in DEsB; is located at the center of Earth and belongs also to the rotating Earth frame E. For this reason the geographic velocity can be defined two ways: vf = DesBe — DEsBj. However, let me caution you that the point E in this context can only be the center of the Earth and not just any point of the Earth frame, as was the case earlier. With this stipulation we formulate the second translational equation:

£>7sB/ = vf + flEIsBI (10.57)

For programming purposes we have to distinguish whether the geographic velocity is given in geodetic or body coordinates. Accordingly, we have two options:

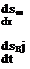= [Г]°/[иІ]° + [П£/]/М/ (10.58)

= [L]B/[uf]5 + [f2£/]/M/ (10.59)

Equations (10.55) and (10.58) constitute the translational equations with emphasis on geodetic coordinates, whereas Eqs. (10.56) and (10.59) focus on the body coordinate system. Both give the same results. It is up to your customer to express her preference. The initialization of the geographic velocity v f may be the deciding factor. [vB]D is easier to visualize than [uf ]B. Yet in any case, you will need to calculate both: [vB]B to derive the incidence angles and [uf ]D to plot the velocity components over the Earth.

The derivation of the attitude equation harbors no surprises. Euler’s law, referred to the inertial frame 7 and expressed in body axes, leads to the same rotational

equations (10.44), already used and repeated here for completeness:

= ([/l]Br1Hn"]B[/2]lV/]B + -тв}в) (10-6°)

The direction cosine matrix is as already calculated from the inertial body rates [coBI]B, Eqs. (10.47-10.49).

Let us list the state variables that are to be integrated: the geographic velocity [uf ]D or [uf]B; the inertial position [sBiY: the inertial body rates [coB,]B – and the direction cosine matrix. Now, the second formulation of the six-DoF equations of motions over an elliptical Earth is complete.

Here are your choices. You can model your hypersonic vehicle relative to the inertial or the geographic frames over an elliptical rotating Earth and exercise several methods of initialization. I recommend the inertial approach because of its simplicity and I would combine it with the direction cosine matrix computations. If your customer requests a spherical Earth instead of its elliptical shape, you can accommodate him easily by setting the flattening parameter to zero and the semimajor axis of the ellipsoid to the mean Earth radius.

As you build your simulation, let the CADAC GHAME6 code be your guide. There you will also find other interesting modeling applications for aerodynamics and autopilots, which are the subject of the following sections.