Category Aerodynamics for Engineering Students

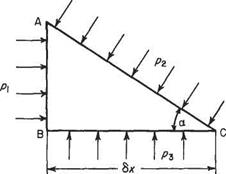
Consider the right prism of length 6z into the paper and cross-section ABC, the angle ABC being a right-angle (Fig. 1.2). The prism is constructed of material of the same density as a bulk of fluid in which the prism floats at rest with the face BC horizontal.

PressuresPi, P2 andрз act on the faces shown and, as proved above, these pressures act in the direction perpendicular to the respective face. Other pressures act on the end faces of the prism but are ignored in the present problem. In addition to these pressures, the weight W of the prism acts vertically downwards. Consider the forces acting on the wedge which is in equilibrium and at rest.

Fig. 1.2 The prism for Pascal’s Law

Resolving forces horizontally,

p (6x tan a)6z —p2(Sx sec a) 6z sin a = 0 Dividing by 6x 6z tan a, this becomes

pi – p2 = 0

i. e.

Pi = P2

Resolving forces vertically,

Рзбхбг — p2(6xssca) fecosa — W = 0

Now

W = pg(6x)2 tan a 6zj2

therefore, substituting this in Eqn (1.2) and dividing by 6x6z,

Ръ ~P2~jPg tan a 6z = 0

If now the prism is imagined to become infinitely small, so that <5jc —► 0 and 6z —у 0, then the third term tends to zero leaving

Ръ ~P2 = 0

Thus, finally,

Pl=P2=P3 (1.3)

Having become infinitely small, the prism is in effect a point and thus the above analysis shows that, at a point, the three pressures considered are equal. In addition, the angle a is purely arbitrary and can take any value, while the whole prism could be rotated through a complete circle about a vertical axis without affecting the result. Consequently, it may be concluded that the pressure acting at a point in a fluid at rest is the same in all directions.

At any point in a fluid, whether liquid or gas, there is a pressure. If a body is placed in a fluid, its surface is bombarded by a large number of molecules moving at random. Under normal conditions the collisions on a small area of surface are so frequent that they cannot be distinguished as individual impacts. They appear as a steady force on the area. The intensity of this ‘molecular bombardment’ force is the static pressure.

Very frequently the static pressure is referred to simply as pressure. The term static is rather misleading. Note that its use does not imply the fluid is at rest.

For large bodies moving or at rest in the fluid, e. g. air, the pressure is not uni­form over the surface and this gives rise to aerodynamic force or aerostatic force respectively.

Since a pressure is force per unit area, it has the dimensions

[Force] + [area] = [MLT-2] [L2] = [ML-1T-2]

and is expressed in the units of Newtons per square metre or Pascals (Nm’2 or Pa).

Pressure in fluid at rest

Consider a small cubic element containing fluid at rest in a larger bulk of fluid also at rest. The faces of the cube, assumed conceptually to be made of some thin flexible material, are subject to continual bombardment by the molecules of the fluid, and thus experience a force. The force on any face may be resolved into two components, one acting perpendicular to the face and the other along it, i. e. tangential to it. Consider for the moment the tangential components only; there are three signifi­cantly different arrangements possible (Fig. 1.1). The system (a) would cause the element to rotate and thus the fluid would not be at rest. System (b) would cause the element to move (upwards and to the right for the case shown) and once more, the fluid would not be at rest. Since a fluid cannot resist shear stress, but only rate of change of shear strain (Sections 1.2.6 and 2.7.2) the system (c) would cause the element to distort, the degree of distortion increasing with time, and the fluid would not remain at rest.

The conclusion is that a fluid at rest cannot sustain tangential stresses, or con­versely, that in a fluid at rest the pressure on a surface must act in the direction perpendicular to that surface.

The basic feature of a fluid is that it can flow, and this is the essence of any definition of it. This feature, however, applies to substances that are not true fluids, e. g. a fine powder piled on a sloping surface will also flow. Fine powder, such as flour, poured in a column on to a flat surface will form a roughly conical pile, with a large angle of repose, whereas water, which is a true fluid, poured on to a fully wetted surface will spread uniformly over the whole surface. Equally, a powder may be heaped in a spoon or bowl, whereas a liquid will always form a level surface. A definition of a fluid must allow for these facts. Thus a fluid may be defined as ‘matter capable of flowing, and either finding its own level (if a liquid), or filling the whole of its container (if a gas)’.

Experiment shows that an extremely fine powder, in which the particles are not much larger than molecular size, will also find its own level and may thus come under the common definition of a liquid. Also a phenomenon well known in the transport of sands, gravels, etc. is that they will find their own level if they are agitated by vibration, or the passage of air jets through the particles. These, however, are special cases and do not detract from the authority of the definition of a fluid as a substance that flows or (tautologically) that possesses fluidity.

1.2.1 Forms of matter

Matter may exist in three principal forms, solid, liquid or gas, corresponding in that order to decreasing rigidity of the bonds between the molecules of which the matter is composed. A special form of a gas, known as a plasma, has properties different from

those of a normal gas and, although belonging to the third group, can be regarded justifiably as a separate, distinct form of matter.

In a solid the intermolecular bonds are very rigid, maintaining the molecules in what is virtually a fixed spatial relationship. Thus a solid has a fixed volume and shape. This is seen particularly clearly in crystals, in which the molecules or atoms are arranged in a definite, uniform pattern, giving all crystals of that substance the same geometric shape.

A liquid has weaker bonds between the molecules. The distances between the molecules are fairly rigidly controlled but the arrangement in space is free. A liquid, therefore, has a closely defined volume but no definite shape, and may accommodate itself to the shape of its container within the limits imposed by its volume.

A gas has very weak bonding between the molecules and therefore has neither a definite shape nor a definite volume, but will always fill the whole of the vessel containing it.

A plasma is a special form of gas in which the atoms are ionized, i. e. they have lost one or more electrons and therefore have a net positive electrical charge. The electrons that have been stripped from the atoms are wandering free within the gas and have a negative electrical charge. If the numbers of ionized atoms and free electrons are such that the total positive and negative charges are approximately equal, so that the gas as a whole has little or no charge, it is termed a plasma. In astronautics the plasma is usually met as a jet of ionized gas produced by passing a stream of normal gas through an electric arc. It is of particular interest for the re-entry of rockets, satellites and space vehicles into the atmosphere.

Having defined the four fundamental dimensions and their units, it is possible to establish units of all other physical quantities (see Table 1.1). Speed, for example, is defined as the distance travelled in unit time. It therefore has the dimension LT-1 and is measured in metres per second (ms-1). It is sometimes desirable and permissible to use kilometres per hour or knots (nautical miles per hour, see Appendix 4) as units of speed, and care must then be exercised to avoid errors of inconsistency.

To find the dimensions and units of more complex quantities, appeal is made to the principle of dimensional homogeneity. This means simply that, in any valid physical equation, the dimensions of both sides must be the same. Thus if, for example, (mass)" appears on the left-hand side of the equation, (mass)" must also appear on the right-hand side, and similarly this applies to length, time and temperature.

Thus, to find the dimensions of force, use is made of Newton’s second law of motion

Force = mass x acceleration

while acceleration is speed -=- time. Expressed dimensionally, this is

Writing in the appropriate units, it is seen that a force is measured in units of kgms-2. Since, however, the unit of force is given the name Newton (abbreviated usually to N), it follows that

1N = 1 kgms 2

It should be noted that there could be confusion between the use of m for milli and its use for metre. This is avoided by use of spacing. Thus ms denotes millisecond while m s denotes the product of metre and second.

The concept of the dimension forms the basis of dimensional analysis. This is used to develop important and fundamental physical laws. Its treatment is postponed to Section 1.4 later in the current chapter.

1.1.1 Imperial units*

Until about 1968, aeronautical engineers in some parts of the world, the United Kingdom in particular, used a set of units based on the Imperial set of units. In this system, the fundamental units were:

mass – the slug length – the foot time – the second

temperature – the degree Centigrade or Kelvin.

Sometimes, the fundamental units defined above are inconveniently large or incon­veniently small for a particular case. In such cases, the quantity can be expressed in terms of some fraction or multiple of the fundamental unit. Such multiples and fractions are denoted by appending a prefix to the symbol denoting the fundamental unit. The prefixes most used in aerodynamics are:

M (mega) – denoting one million к (kilo) – denoting one thousand m (milli) – denoting one one-thousandth part H (micro) – denoting one-millionth part

Thus

1MW= 1000 000W 1 mm = 0.001 m 1 /лп 0.001 mm

A prefix attached to a unit makes a new unit. For example,

1mm2 = 1 (mm)2 = 10_6m2, not 10-3m2 For some purposes, the hour or the minute can be used as the unit of time.

There are four fundamental dimensions in terms of which the dimensions of all other physical quantities may be expressed. They are mass [M], length [L], time [T] and temperature [ff J A consistent set of units is formed by specifying a unit of particular value for each of these dimensions. In aeronautical engineering the accepted units are respectively the kilogram, the metre, the second and the Kelvin or degree Celsius (see below). These are identical with the units of the same names in common use, and are defined by international agreement.

It is convenient and conventional to represent the names of these units by abbreviations:

kg for kilogram m for metre s for second °С for degree Celsius К for Kelvin

The degree Celsius is one one-hundredth part of the temperature rise involved when pure water at freezing temperature is heated to boiling temperature at standard pressure. In the Celsius scale, pure water at standard pressure freezes at 0 °С and boils at 100 °С.

The unit Kelvin (K) is identical in size with the degree Celsius (°С), but the Kelvin scale of temperature is measured from the absolute zero of temperature, which is approximately —273 °С. Thus a temperature in К is equal to the temperature in °С plus 273 (approximately).

A study in any science must include measurement and calculation, which presupposes an agreed system of units in terms of which quantities can be measured and expressed. There is one system that has come to be accepted for most branches of science and engineering, and for aerodynamics in particular, in most parts of the world. That system is the Systeme International d’Unites, commonly abbreviated to SI units, and it is used throughout this book, except in a very few places as specially noted.

It is essential to distinguish between the terms ‘dimension’ and ‘unit’. For example, the dimension ‘length’ expresses the qualitative concept of linear displacement, or distance between two points, as an abstract idea, without reference to actual quantitative measurement. The term ‘unit’ indicates a specified amount of the quantity. Thus a metre is a unit of length, being an actual ‘amount’ of linear displacement, and

so also is a mile. The metre and mile are different units, since each contains a different amount of length, but both describe length and therefore are identical dimensions[1] Expressing this in symbolic form:

x metres = [L] (a quantity of x metres has the dimension of length) x miles = [L] (a quantity of x miles has the dimension of length) x metres Ф x miles (x miles and x metres are unequal quantities of length)

[х metres] = [x miles] (the dimension of x metres is the same as the dimension of x miles).

Preamble

The study of aerodynamics, as is the case with that of all physical sciences and technologies, requires the common acceptance of a number of basic definitions including an unambiguous nomenclature and an understanding of the relevant physical properties, the related mechanics and the appropriate mathematics.

Of course, many of these are common to other disciplines and it is the purpose of this chapter to identify and explain those that are basic and pertinent to aerodynamics and which are to be used in the remainder of the volume.

The units and dimensions of all physical properties and the relevant properties of fluids are recalled, and after a review of the aeronautical definitions of wing and aerofoil geometry, the remainder of the chapter introduces aerodynamic force.

The origins of aerodynamic force and how it is manifest on wings and other aeronautical bodies and the theories that permit its evaluation and design are to be found in the remainder of the volume, but in this chapter the lift, drag, side-wind components and associated moments of aerodynamic force are conventionally identified, the application of dimensional theory establishing their coefficient form. The significance of the pressure distribution around an aero­dynamic body and the estimation of lift, drag and pitching moment on it in flight, completes this chapter of basic concepts and definitions.

This volume is intended for students of engineering on courses or programmes of study to graduate level.

The sequence of subject development in this edition commences with definitions and concepts and goes on to cover incompressible flow, low speed aerofoil and wing theory, compressible flow, high speed wing theory, viscous flow, boundary layers, transition and turbulence, wing design, propellers and propulsion.

Accordingly the work deals first with the units, dimensions and properties of the physical quantities used in aerodynamics then introduces common aeronautical definitions before explaining the aerodynamic forces involved and the basics of aerofoil characteristics. The fundamental fluid dynamics required for the develop­ment of aerodynamics and the analysis of flows within and around solid boundaries for air at subsonic speeds is explored in depth in the next two chapters, which continue with those immediately following to use these and other methods to develop aerofoil and wing theories for the estimation of aerodynamic characteristics in these regimes. Attention is then turned to the aerodynamics of high speed air flows. The laws governing the behaviour of the physical properties of air are applied to the transonic and supersonic regimes and the aerodynamics of the abrupt changes in the flow characteristics at these speeds are explained. The exploitation of these and other theories is then used to explain the significant effects on wings in transonic and supersonic flight respectively, and to develop appropriate aerodynamic characteris­tics. Viscosity is a key physical quantity of air and its significance in aerodynamic situations is next considered in depth. The useful concept of the boundary layer and the development of properties of various flows when adjacent to solid boundaries, build to a body of reliable methods for estimating the fluid forces due to viscosity and notably, in aerodynamics, of skin friction and profile drag. Finally the two chapters on wing design and flow control, and propellers and propulsion respectively, bring together disparate aspects of the previous chapters as appropriate, to some practical and individual applications of aerodynamics.

It is recognized that aerodynamic design makes extensive use of computational aids. This is reflected in part in this volume by the introduction, where appropriate, of descriptions and discussions of relevant computational techniques. However, no comprehensive cover of computational methods is intended, and experience in computational techniques is not required for a complete understanding of the aerodynamics in this book.

Equally, although experimental data have been quoted no attempt has been made to describe techniques or apparatus, as we feel that experimental aerodynamics demands its own considered and separate treatment.

We are indebted to the Senates of the Universities and other institutions referred to within for kindly giving permission for the use of past examination questions. Any answers and worked examples are the responsibility of the authors, and the author­ities referred to are in no way committed to approval of such answers and examples.

This preface would be incomplete without reference to the many authors of classical and popular texts and of learned papers, whose works have formed the framework and guided the acquisitions of our own knowledge. A selection of these is given in the bibhography if not referred to in the text and we apologize if due recognition of a source has been inadvertently omitted in any particular in this volume.

ELH/PWC

2002