Die wichtigste Folge aus der Bildung dieser freien Wirbel besteht darin, daB im Gegensatz zum Fliigel unendlicher Spannweite der Trag – fliigel endlicher Spannweite auch in reibungsloser Stromung einen Widerstand erfahrt [induzierter Widerstand). Physikalisch laBt sich dieser induzierte Widerstand durch das Einrollen der Trennungsflache zu den
beiden freien Wirbeln erklaren: In jedem Zeitabschnitt muB ein Stuck dieser beiden freien Wirbel neu gebildet werden. Hierftir muB dauernd
|
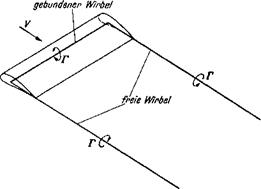
Abb. 7.2. Wirbelsystem eines Tragfliigels endlicher Spannweite (Hufeisenwirbel).
|
Arbeit geleistet werden, die als kinetische Energie in den Wirbelzopfen enthalten ist. Das Aquivalent fur diese Arbeit steckt in der tlberwindung des Widerstandes bei der Vorwartsbewegung des Tragfliigels.
Andererseits laBt sich das Zustandekommen des induzierten Widerstandes auch mittels des Kutta-Joukowskyschen Satzes folgender – maBen einsehen:
Die nach hinten abgehenden freien Wirbel erzeugen hinter dem Tragfliigel und am Ort des Tragfliigels nach Biot-Savart eine Ab-
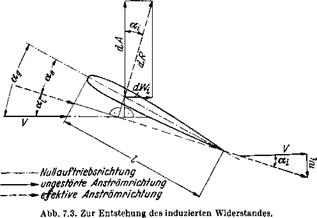
wartsgeschwindigkeit wh Abb. 7.3. Am Ort des Fliigels setzt sich so – mit die resultierende Anstromungsgeschwindigkeit des Fliigelprofils aus der Anstromgeschwindigkeit V und dieser induzierten Abwartsge-
schwindigkeit zusammen. Die resultierende Anstromrichtung am Ort des Fliigels ist gegeniiber der ungestorten Anstromrichtung somit um den Winkel oc( nach abwarts geneigt, wobei ist. Es ist im allgemeinen V und somit ос( ^ sin#* ^ tan at*.
Nach dem Satz von Kutta-Joukowsky, Кар. 6.11, ist die resultierende Luftkraft dR am Fliigelschnitt у (Abb. 7.3) senkrecht zur resultierenden Anstromrichtung. Sie hat somit senkrecht zur ungestorten Anstromrichtung die Auftriebskomponente dA — dR cosoq ^ dR und parallel zur ungestorten Anstromrichtung die Widerstandskomponente dWі = dR sin oc( ^ dR a,-. Letzteres ist der induzierte Widerstand des Fliigelschnittes y. Mit Beriicksichtigung von Gl. (7.1) ist
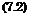 dWi = dAoci — dA ^r.
dWi = dAoci — dA ^r.
Den gesamten induzierten Widerstand erhalt man hieraus durch Integration liber die Fliigelspannweite von у = —6/2 bis у — +6/2, somit
6/2
Wt = yfjiw‘Mdy – <7-3>
—6/2
Dabei bedeutet dAjdy den Auftrieb pro Langeneinheit der Spannweite und Wi(y) die im allgemeinen langs Spann weite veranderliche Ver – teilung der induzierten Abwartsgeschwindigkeit. Fur das einfache Modell des Hufeisenwirbels (Abbildung 7.2) ergibt sich fur die durch die beiden freien Wirbel hervorgerufene Verteilung der Abwartsgeschwindigkeit am Ort des Tragfliigels durch Anwendung des Biot-Savartschen Gesetzes, Кар. 2.46:
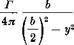
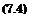 u>i(y) =
u>i(y) =
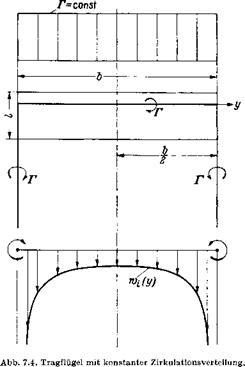
Diese Abwindverteilung ist in Abb. 7.4 dargestellt. Hierbei hat die induzierte Abwartsgeschwindigkeit in Fliigelmitte ein Minimum, wahrend sich an den Fliigelenden у — + 6/2 bei Annaherung an die freien Wirbel unendhch groBe Werte ergeben.
Das stark vereinfachte Wirbelmodell nach Abb. 7.4 mit konstanter Zirkulationsverteilung langs Spannweite und zwei freien Einzelwirbeln an den beiden Fliigelenden reicht jedoch noch nicht aus, um den induzierten Widerstand nach Gl. (7.3) quantitativ zu ermitteln. Vielmehr ist es daftir erforderlich, das Modell der vom Tragfliigel abgehenden
freien Wirbel zu verfeinern. Der oben erwahnte Druckausgleich um die Fliigelenden herum bewirkt, daB der Auftrieb und damit auch die Zirkulation in der Nahe der Fliigelenden starker abgemindert wird als in der Fliigelmitte. An den Fliigelenden selbst tritt sogar vollkommener
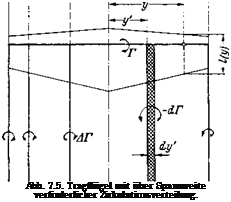
Ausgleich des Druckunterschiedes zwischen Unter – und Oberseite und damit ein Abfall der Zirkulation auf Null ein. Die wirkliche Zirkulations- verteilung ist von der Art, wie in Abb. 7.5 dargestellt; sie ist mit der Spannweitenkoordinate veranderlich, Г — Г (у). Zwischen dem Auftrieb dA eines Fliigelstuckes der Breite dy und dessen Zirkulation Г{у) besteht nach Kutta-Joukowsky der Zusammenhang, vgl. Gl. (6.1),
dA = qV Г (y) dy. (7.5)
Damit ergibt sich aus Gl. (7.3) fur den induzierten Widerstand:
6/2
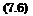 = qJ Г(у) Wi(y)dy.
= qJ Г(у) Wi(y)dy.
— bj%
Den gesamten Auftrieb erhalt man durch Integration von Gl. (7.5) zu:
6/2
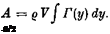 (7.7)
(7.7)
Die veranderliche Zirkulationsverteilung T(y) nach Abb. 7.5 kann man sich durch eine treppenformige Verteilung ersetzt denken. Fur letztere
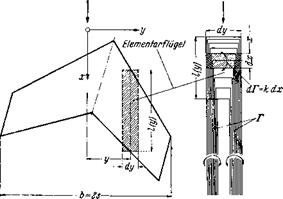
entsteht jeweils am Ort der Treppenstufe ein nach hinten abgehender freier Wirbel der Starke А Г. Im Grenziibergang von der treppenformigen Zirkulationsverteilung zur stetigen Zirkulationsverteilung ergibt sich dann fiir die freien Wirbel eine flachenhafte Verteilung (Wirbelflache). Ein Streifen dieser Wirbelflache der Breite dy hat dabei die Zirkulations – starke dr = (dTjdy) dy. Somit gibt die Neigung der Zirkulationsverteilung Г(у) des gebundenen Wirbels die Verteilung der Wirbelstarke in der freien Wirbelflache an.
Die Verteilung der induzierten Abwartsgeschwindigkeit langs Spannweite erhalt man durch Anwendung des Biot-Savartschen Gesetzes auf die vom Fliigel abgehenden freien Wirbel. Der Beitrag des Wirbel – streifens dy’ an der Stelle y’ zur Abwartsgeschwindigkeit am Ort der tragenden Linie у (Abb. 7.5) betragt nach Gl. (2.163):
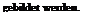 Hieraus findet man durch Integration iiber die Wirbelflache fur die induzierte Geschwindigkeit am Ort des Fliigels :[1]
Hieraus findet man durch Integration iiber die Wirbelflache fur die induzierte Geschwindigkeit am Ort des Fliigels :[1]
6/2
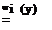
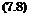 1 r dr dy’
1 r dr dy’
4 n J dy’ у — у’ —6/2
Nach dieser Gleichung kann die induzierte Abwartsgeschwindigkeit w{(y) am Ort der tragenden Linie berechnet werden, wenn die Zir- kulationsverteilung Г(у) vorgegeben ist. Damit kann man den indu – zierten Widerstand nach Gl. (7.6) ermitteln.
Es sei hier bereits angemerkt, daB sehr weit hinter dem Fliigel die induzierte Abwartsgeschwindigkeit doppelt so groB ist wie die induzierte Abwartsgeschwindigkeit am Ort des Fliigels nach Gl. (7.8), vgl. Кар. XI:
Лу) = -2 Wi{y). (7.8a)
Die Geschwindigkeit wird positiv in Richtung der positiven z-Achse gerechnet, Ygl. Abb. 7.19.
7.13 Prandtlsche Integralgleichung fiir die Zirkulations – verteilung
Die obigen Vorstellungen sollen jetzt dazu benutzt werden, um eine Gleichung aufzustellen, mittels derer fiir einen vorgegebenen Tragfliigel endhcher Spannweite die Zirkulationsverteilung langs Spannweite er – mittelt werden kann.
Die in Abb. 7.3 erlauterte Anderung der Anstromrichtung infolge der von den freien Wirbeln induzierten Abwartsgeschwindigkeit fiihrt dazu, daB ein Tragflugelschnitt у des Tragfliigels endhcher Spannweite beim geometrischen Anstellwinkel ocg einen geringeren Auftrieb erfahrt als der gleiche Tragfliigelschnitt bei unendhcher Spannweite. Fiir ein Flachenelement dy eines Tragfliigels endhcher Spannweite be – tragt der Auftrieb:
dAz= 2 dy C“^ = 2 V4^ dy C®°° (7-9)
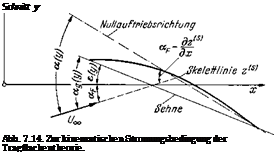
Dabei bedeutet l(y) die Fliigeltiefe an der Stelle у {Abb. 7.5) und ca(y) — c’aoo&eiy) den ortlichen Auftriebsbeiwert des Flachenelementes dF = l(y)dy. Man bezeichnet oce(y) als den effektiven Anstellwinkel (Abb. 7.3) und c’ go = (dcaldoc)00 als den Auftriebsanstieg fur den Trag – fliigel unendlicher Spannweite. Letzterer ist nach der Theorie diinner Profile nahezu gleich 2л, vgl. Кар. VI. Fur die angestellte ebene Platte gilt exakt c’aoo = 2л. Der Gl. (7.9) liegt die Vorstellung zugrunde, daB der Profilschnitt des Tragfliigels endlicher Spannweite sich so verhalt wie ein solcher beim Fliigel unendlicher Spannweite, der mit dem Anstellwinkel oce angestromt wird.
Zwischen dem von der Nullauftriebsrichtung aus gemessenen geo – metrischen Anstellwinkel <xg(y), diesem effektiven Anstellwinkel oce(y) und dem in Gl. (7.1) erlauterten induzierten Anstellwinkel ос{(у) besteht nach Abb. 7.3 der Zusammenhang
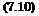 <Xg{y) = *e(y) + OCi(y).
<Xg{y) = *e(y) + OCi(y).
Ersetzt man in Gl. (7.9) dA durch Gl. (7.5), dann ergibt sich fur den effektiven Anstellwinkel
Weiterhin gilt fur den induzierten Anstellwinkel mit =■ w{V nach Gl. (7.8):

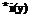
(7.12)
Dieses ist die Prandtlsche Integralgleichung fur die Zirkulationsverteilung des Tragfliigels endhcher Spannweite, wie sie von Prandtl zuerst im Jahre 1918 angegeben wurde [61]. Sie ist eine hneare Integralgleichung fur die Zirkulationsverteilung Г(у), wobei Г hnear vom Anstellwinkel ocg abhangt. Der Profilbeiwert c’aoo ist aus der Profiltheorie (Кар. VI) bekannt.[2]
Bei vorgegebener Fliigelgeometrie [Fliigeltiefenverteilung l(y) und Anstellwinkelverteilung <xg(y)] laBt sich aus Gl. (7.13) die Zirkulations –
verteilung Г(у) ermitteln. Dieses ist die sog. Nachrechnungsaufgabe (zweite Hauptaufgabe) der Tragfliigeltheorie.
Ist dagegen die Zirkulationsverteilung Г(у) bekannt, so laBt sich aus Gl. (7.13) entweder bei vorgegebener Tiefenverteilung l(y) die Anstellwinkelverteilung (Verwindungswinkel) ocg(y) oder bei vorgegebener Anstellwinkelverteilung ocg(y) die Tiefenverteilung l(y) ermitteln. Dieses ist die sog. Entwurfsaufgabe (erste Hauptaufgabe) der Tragfliigeltheorie.
In beiden Fallen ergibt sich der Auftrieb nach Gl. (7.7) und der indu – zierte Widerstand nach Gl. (7.6) aus der Zirkulationsverteilung Г(у). Vom mathematischen Standpunkt aus ist die zweite Hauptaufgabe wesentlich schwieriger als die erste Hauptaufgabe, da bei der zweiten Hauptaufgabe eine Integralgleichung zu losen ist, wahrend bei der ersten Hauptaufgabe nur Quadraturen auszufiihren sind.
7.14 Elliptische Zirkulationsverteilung
Eine besonders einfache Losung von Gl. (7.13), die auch groBe prak – tisehe Bedeutung hat, ergibt sich fiir die elliptische Zirkulationsver-

 teilung langs Spannweite.
teilung langs Spannweite.
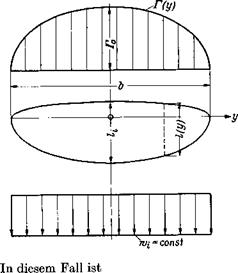
Г(у) = Г0^1-(^-) (7.14)
wobei Г0 die Zirkulation in Fliigelmitte у – 0 bedeutet, Abb. 7.6. Nach Gl. (7.7) erhalt man fiir den Auftrieb:
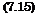 A = y gbVГ0.
A = y gbVГ0.
Die induzierte Abwartsgeschwindigkeit ergibt sich nach Gl. (7.8) zu
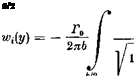 ______ dy’
______ dy’
^y’J y-yr
Die Ausrechnung dieses Integrals liefert fur Punkte innerhalb der Spannweite, y < 6/2 d
wdy) = (7.16)
Man findet das bemerkenswerte Ergebnis, daB bei elliptischer Zir- kulationsverteilung die induzierte Abwartsgeschwindigkeit w{ und da – mit auch der induzierte Anstellwinkel oc{ langs der Spannweite konstant ist (Abb. 7.6).
Setzt man die Gin. (7.14) und (7.16) in Gl. (7.6) ein, dann erhalt man Mr den induzierten Wider stand:
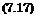 Wi = f oFfy
Wi = f oFfy
Mit jT0 nach Gl. (7.15) ergibt sich der folgende Zusammenhang zwischen dem induzierten Widerstand und dem Auftrieb:
Dabei bedeutet q = (p/2) V2 den zur Anstromgeschwindigkeit V ge – horigen Staudruck (Geschwindigkeitsdruck). Es ist der induzierte Widerstand proportional dem Quadrat des Auftriebes sowie umgekehrt proportional dem Staudruck und dem Quadrat der Spannweite.
Fur den induzierten Anstellwinkel ос і = w^V erhalt man nach den Gin. (7.16) und (7.15):
<*dy) = = const. (7-19)
nqbй
1 Zur Auswertung des Integrals macht man zweckmaBigerweise die Substitution 2y’/b = cos Damit laBt sich das Integral iiberfuhren in die Form
/
vgl. Gl. (6.73).
Durch Vergleich der Gin. (7.18) und (7.19) bestatigt man die friiher in Gl. (7.2) angegebene Beziehung W( — ос(А.
Die Geometrie des zugehorigen Fliigels ergibt sich besonders einfach, wenn man einen unverwundenen Fliigel zugrunde legt, ag(y) = ocg = = const. Da nach Gl. (7.19) der induzierte Anstellwinkel <%* (y) = const ist, folgt nach Gl. (7.10), daB auch der effektive Anstellwinkel langs Spannweite konstant sein muB, ae(y) = const. Daraus ergibt sich nach den Gin. (7.11) und (7.14), daB die Fliigeltiefe langs der Spannweite elliptisch verteilt ist:
%) = *ij/l – (y)2- (7-20)
Der elhptische FlugelgrundriB ist in Abb. 7.6 dargestellt.[3] Somit ist gezeigt, daB die elhptische Zirkulationsverteilung bei einem unverwundenen Ellipsenfliigel vorliegt. Fiir diesen ist nach Gl. (7.9) dann auch der orthche Auftriebsbeiwert ca(y) langs der Spannweite konstant.
Beiwerte. SchlieBlich mogen die wichtigen Ergebnisse fur den indu- zierten Anstellwinkel nach Gl. (7.19) und fiir den induzierten Widerstand nach Gl. (7.18) noch durch die dimensionslosen Beiwerte fiir den Auf – trieb und den induzierten Widerstand ausgedriickt werden. Diese sind wie folgt definiert:
A = cAqF, (7.21)
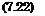 W і = cwiqF
W і = cwiqF
mit F als FliigelgrundriBflache.
Damit ergibt sich aus den Gin. (7.19) und (7.18):
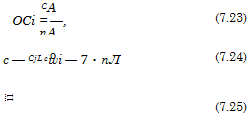 Hierin bedeutet
Hierin bedeutet
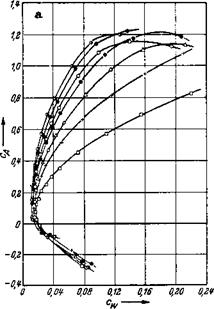
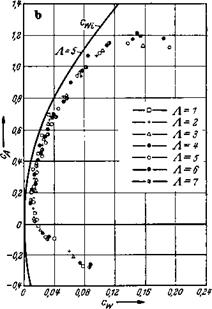
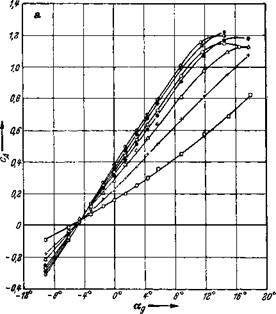
das Seitenverhaltnis des Fliigels nach Gl. (5.4). Das wichtige Ergebnis fiir den Beiwert des induzierten Widerstandes nach Gl. (7.24) ist in Abb. 7.7 fiir einen Fliigel vom Seitenverhaltnis Л = 5 mit MeBergeb – nissen verglichen. Man sieht, daB die theoretische Kurve fiir den induzierten Widerstandsbeiwert die gemessene Polare im ganzen c^-Bereich recht gut wiedergibt. Der Unterschied der beiden Kurven ist iiber dem
ganzen c^-Bereich nahezu konstant. Er riihrt her von dem in der vor – liegenden Theorie vernachlassigten EinfluB der Reibung. Abb. 7.7 legt
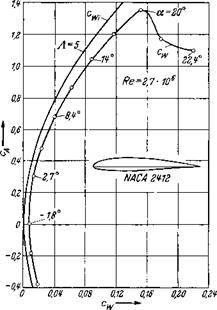 Abb. 7.7. Gemessene Polare eines Tragfltigels vom Seitenverhaltnis /1 = 5 und theoretische Kurve fur den induzierten Widerstand, cWi = /яЛ.
Abb. 7.7. Gemessene Polare eines Tragfltigels vom Seitenverhaltnis /1 = 5 und theoretische Kurve fur den induzierten Widerstand, cWi = /яЛ.
es nahe, den Widerstandsbeiwert aufzuteilen in einen vom Auftriebs – beiwert nahezu unabhangigen Anteil, den man als Beiwert des Profil – widerstandes cWp bezeichnet, und in einen vom Auftriebsbeiwert abhan – gigen Anteil, den Beiwert des induzierten Widerstandes cwi:
cw = cWp – f – cwi (7.26a)
oder wegen Gl. (7.24):
cw = cWp + (7.26 b)
Fiir den geometrischen Anstellwinkel ergibt sich nach den Gin. (7.10) und (7.23):
^ = Ле + й – (7-27)
Dabei ist nach Gl. (7.9) oce = cAJc’Aoo, weil der konstante ortliche Auftriebsbeiwert ca(y) = const und der Gesamtauftriebsbeiwert cA im vor – liegenden Fall gleich sind.
Die letztere Gleichung gestattet es, den Auftriebsanstieg des Trag- fliigels endlicher Spannweite in seiner Abhangigkeit vom Seitenverhalt-
nis zu ermitteln. Aus Gl. (7.27) ergibt sich
Fur cAoo = 2л folgt:
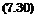 c’a = л c’a oo Л. – J – 2
c’a = л c’a oo Л. – J – 2
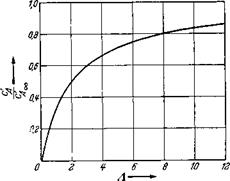
wobei c’A = dcAldocg ist. Gl. (7.30) gibt an, urn wieviel der Auftriebs – anstieg und damit auch der Auftrieb bei gleichem Anstellwinkel infolge des endlichen Seitenverhaltnisses abgemindert wird. In Abb. 7.8 ist
dieses Verhaltnis der Auftriebsanstiege in Abhangigkeit vom Seitenverhaltnis dargestellt.
Wie spater noch genauer gezeigt werden wird, sind die hier fxir den elliptischen Tragfliigel gefundenen Formeln fiir den induzierten Wider – stand und den Auftriebsanstieg auch fiir andere Fliigelformen mit sehr guter Naherung giiltig. Dieses gilt insbesondere auch fiir Rechteck – fliigel, wie A. Betz [1] gezeigt hat, vgl. Abb. 7.30 und Abb. 7.55.
![]() (7.37)
(7.37)![]() 0(x, y y) = 2 J k(x’, y) dx’.
0(x, y y) = 2 J k(x’, y) dx’.










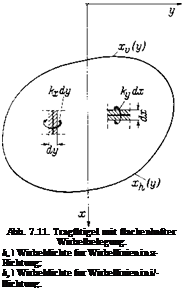 Die Verteilung der Wirbelstarke iiber eine vorgegebene Flache kann in verschiedener Weise erfolgen. Es sei eine Tragfltigelflache von beliebiger Gestalt vorgegeben. Wir wahlen ein rechtwinkliges, fltigelfestes Koordi- natensystem so, daB die y-Achse senkrecht zur Anstromrichtung steht.
Die Verteilung der Wirbelstarke iiber eine vorgegebene Flache kann in verschiedener Weise erfolgen. Es sei eine Tragfltigelflache von beliebiger Gestalt vorgegeben. Wir wahlen ein rechtwinkliges, fltigelfestes Koordi- natensystem so, daB die y-Achse senkrecht zur Anstromrichtung steht.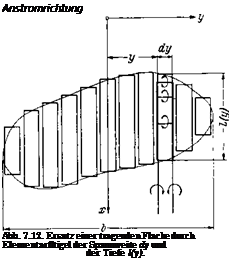


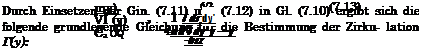

 teilung langs Spannweite.
teilung langs Spannweite. ______ dy’
______ dy’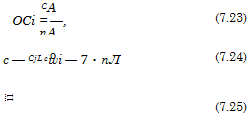 Hierin bedeutet
Hierin bedeutet Abb. 7.7. Gemessene Polare eines Tragfltigels vom Seitenverhaltnis /1 = 5 und theoretische Kurve fur den induzierten Widerstand, cWi = /яЛ.
Abb. 7.7. Gemessene Polare eines Tragfltigels vom Seitenverhaltnis /1 = 5 und theoretische Kurve fur den induzierten Widerstand, cWi = /яЛ.