Although aerofoils of the NACA 6-series, mentioned above, have now largely been replaced by more modern designs, it is worth looking at them in some detail, because a considerable amount of experimental data has been acquired for them. The conclusions that can be drawn are generally applicable to other families of aerofoils.
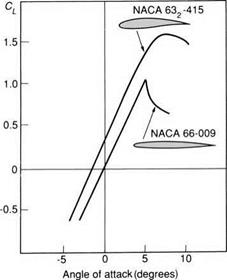
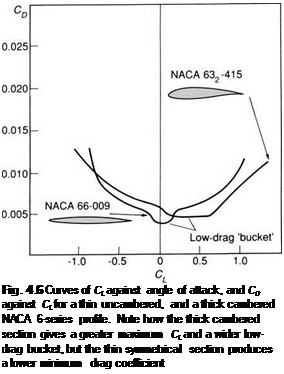
Figure 4.6 shows the lift and drag coefficient curves for two aerofoils of this type. It will be seen that there is a short central dip or ‘bucket’ shape in the drag curve. This represents the conditions where the desired laminar boundary layer occurs, giving low drag. For efficient cruising, the wing section must be operated in the ‘bucket’ region.
As with other NACA aerofoil families, the designation number of 6-series aerofoils gives the most important features in coded form. The system of coding is complicated, but is described by Abbott and von Doenhoff (1949), who also give details of earlier series NACA sections.
In the example given in Fig. 4.5(b), the second number indicates that a favourable pressure gradient on the upper surface exists up to 5 tenths of the chord, i. e. half way along. This is near the position of maximum thickness. The normal range for this position is between 3 and 6 tenths of the wing chord. Moving the position of maximum thickness rearward reduces the value of the minimum drag coefficient, but narrows the range of angle of attack over which low-drag laminar flow can be maintained. It also reduces the maximum lift coefficient that can be obtained, as a long region of unfavourable pressure gradient develops at high angles of attack.
Because of the restricted range of efficient operating conditions, and practical difficulties in maintaining laminar flow over a large proportion of the surface, aerofoils with the maximum thickness point aft of about 50 per cent are only suitable for rather specialised applications.
A whole family of aerofoils having the same basic profile, but with different ratios of maximum thickness to chord, can be drawn. The last two figures in the NACA code indicate the percentage thickness-to-chord ratio.
Reducing the thickness-to-chord ratio has a similar effect to moving the maximum thickness point rearwards. The minimum drag coefficient falls with decreasing thickness, but the maximum lift coefficient is reduced, together with the width of the low-drag laminar bucket.
From Fig. 4.7, it is easy to see why the latter two effects occur. For a thin aerofoil, once the angle of attack is increased by more than a few degrees, the region of favourable pressure gradient on the upper surface decreases rapidly, with a consequential reduction in the proportion of laminar boundary layer. At high angles of attack, the thin nose is likely to provoke leading-edge separation.
|
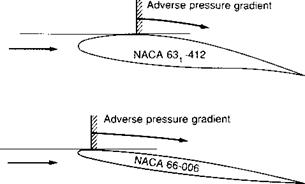
Fig. 4.7 Effect of thickness
A 12 per cent thick NACA 63,-412, and a 6 per cent thick NACA 66-006 section at 8° incidence
On the thin section, the unfavourable pressure gradient starts almost at the nose, and the section is on the point of stalling. The thicker cambered section stalls at around 15°
|
Thick aerofoils thus give a bigger range of low-drag operating conditions, with improved maximum lift coefficient, but at the expense of a slightly increased minimum drag coefficient. The thicker aerofoil also allows deeper spars to be used, with a consequential saving in weight.
The design lift coefficient for this type of section is the value of lift coefficient that corresponds to the middle of the low-drag laminar bucket in the CL to CD curve (Fig. 4.6). The design lift coefficient can be changed by altering the camber. A cambered profile is simply a ‘bent’ version of the basic symmetrical shape. Increasing the camber increases the design value of CL, and maximum CL, and slightly increases the drag coefficient. Increasing the camber also has a destabilising effect, as we shall see later.
For a symmetrical section, the minimum drag coefficient occurs at zero angle of attack, which makes such aerofoils suitable for use on tail surfaces which are required to produce very little lift in level flight.
On earlier wing sections, the shape of the mean line (the camber line) had no real theoretical basis, and a simple mathematical function was used to draw a smooth curve. On nearly all early aerofoils, most of the lift force was concentrated well forward when operating at the design angle of attack. Because a theoretical design method was used for the NACA 6-series aerofoils, it became possible to derive mean lines (camber lines) that would give any desired chord – wise lift force distribution, at a specified angle of attack. In particular, it is possible to use a mean line that gives a nearly constant chordwise distribution of lift at the design lift coefficient. As we shall see later, this is useful for aircraft that fly at high subsonic speeds.
The theoretical method used for the 6-series aerofoils was based on inviscid (no viscosity) flow theory. The effects of viscosity were allowed for by using boundary layer theory, but before the introduction of computers, the accuracy of the procedures was limited, and they were slow and extremely tedious. The aerofoils did not behave exactly as predicted, and had to be carefully tested.
The use of computer-based numerical analysis has produced improved theoretical design procedures, which have led to the development of new generations of aerofoil sections, both for low speed and high speed flight. These aerofoils have generally better characteristics than the earlier 6-series sections, in terms of low drag, and range of operating conditions. Figure 4.8 shows a newer general purpose aerofoil, the NASA LS(1)-0417 (originally designated GA(W)-1), described in detail by McGhee and Beasley (1973). This section has a maximum CL value greater than 2, which is roughly 50 per cent greater than
|

Fig. 4.8 NASA LS(1)-0417 aerofoil intended for general aviation use
A modern aerofoil giving a high maximum CL and a good lift to drag ratio despite a thickness-to-chord ratio of 17 per cent
|
|

Fig. 4.9 Low-drag features on the Optica included end-plate effect on the tail, and a modern low-drag wing section
|
for the equivalent 6-series aerofoil. It has a maximum ratio of lift to drag of around 85. The section has been used on a number of small aircraft, including the Piper Tomahawk, and the Optica, shown in Fig. 4.9.
For transonic aircraft, the wing section geometry is strongly influenced by consideration of the effects of compressibility, and this leads to rather different aerofoil shapes, as described in Chapter 9.
It is important to realise that CL and CD curves such as those given in Fig. 4.6 only apply to two-dimensional sections. The CD values take no account of the trailing vortex drag that occurs on a complete wing. A section that achieves its minimum two-dimensional CD value at a high CL may produce a large overall wing CD because of the contribution due to trailing vortex drag. It should also be noted, that CL and CD values may vary significantly with Reynolds number, and many of the older sections were only tested at relatively low Reynolds numbers.
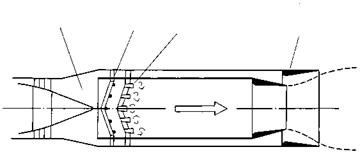 Fig. 6.30 A reheat chamber or afterburner
Fig. 6.30 A reheat chamber or afterburner