Category Aircraft Flight

For the most part, the flight of an aircraft can be divided into at least three dis­tinct phases – take-off and climb, cruise, descent and landing. In this chapter we will be primarily concerned with the cruise performance of the aircraft. Landing and take-off will be discussed later in Chapter 13.

The nature of the cruise will change depending on the use to which the aircraft is to be put. For example, a commercial airliner must operate as eco­nomically as possible, and so reducing fuel usage over a given route is of prime importance. However, as we shall see later, this is not the only factor that matters as far as the operator is concerned. For a patrol aircraft, such as the airborne radar system, AWACS, or a Police observation aircraft (Figs 7.3 and 4.9) endurance is likely to be the overriding consideration. For a fighter it may well be a combination of high speed, in order to make an interception, coupled with a need for either range or endurance, depending on the particular mission undertaken. In this case the ‘cruise’ phase of the flight can be subdivided. This is also true of other aircraft types. For instance, a commercial airliner must frequently spend some time in waiting its turn to land at a busy airport, and so an important ‘stand off’ phase is introduced, which is required purely for organisational purposes.

In the rocket-launched vehicles described above a considerable part of the mass at the start of the flight is the oxidant which must be carried in order to burn the fuel. A large proportion of this is used within the atmosphere and so con­siderable savings are possible if an air-breathing engine and aerodynamic lift can be used for the preliminary stages of the flight.

The object of the exercise is defeated, however, if an additional engine has to be carried instead of the fuel. The use of a dual mode engine, such as the turbo-rocket described in Chapter 6, provides a possible solution. The weight saving is sufficient to allow the use of a single stage to achieve earth orbit, with considerable savings in operating costs. The ‘Skylon’ vehicle (Fig. 8.20) is a proposal based on an advanced form of this type of engine. €1m of funding for further development of this project was annouced in 2009.

For spacecraft designed to make just a short duration journey outside the Earth’s atmosphere and at less than the speed needed for an orbit (sub-orbital spaceflight) a practical solution is to launch it from a conventionally-powered mother ship. This cost-effective, approach has been adopted for the Virgin Galactic Spaceship Two with its White Knight mother ship. The intention of this project is to open up a new market in ‘space tourism’, with the ultimate possibility of achieving high-speed long-range commercial transportation.

Powered controls may take two forms, servo-assisted, or fully power operated. In the former type, hydraulic pressure is transmitted via pipes to a servo – actuator which helps the mechanical linkage to move the surface. The mechan­ical linkage can be used to operate the control surface, even if power is lost, although the controls will then feel very heavy. The system is similar to the servo-assisted steering and braking system of a car.

Power control, fly-by-wire and fly-by-light

In pure power operation, no mechanical override is provided. Control signals may be transmitted hydraulically, directly from valves attached to the control column, or electrically to actuators, which move the control surfaces. The lat­ter system is known as fly-by-wire. The actuators are electrically or hydraulic­ally operated rams or motors.

As an alternative to electrical signal transmission, modulated light signals may be transmitted along optical fibres. This system is known as fly-by-light

and overcomes problems due to electromagnetic interference. The detonation of nuclear weapons would cause very strong electromagnetic signals capable of upsetting, if not destroying, conventional electronic circuits. The deliberate jamming of electronic circuitry by means of powerful electromagnetic beams is also a possibility, and some military aircraft have been found to be very vulnerable in this respect.

Once control by electrical signals is accepted, it becomes convenient to incorporate sophisticated electronic processing into the circuit, with increas­ing emphasis on digital systems. Such processing can be used to alter the response to control inputs, and can allow for manoeuvres such as flying in a stalled or an unstable condition, or approaching very close to the stall on landing.

Fly-by-wire can thus dramatically improve the performance, efficiency and even safety of aircraft. It also allows for co-ordinated control surface move­ments that would be too complex for a pilot to manage unaided. Such systems have demonstrated a high level of reliability and are being increasingly used. On military aircraft, the flight control, autostabilisation, navigation, radar and weapons control systems are all integrated in varying degrees.

The second of the lateral motions which we shall consider is also non­oscillatory, but this time it turns out that for most aircraft it is either very weakly damped or sometimes divergent with time. Some aircraft are so near the boundary of stability that the motion may, due to asymmetry of trim or engines, be just stable in one direction but slightly divergent in the other.

The motion is a combination of yaw and sideslip. Let us first examine the way in which the various forces and moments which influence this motion are generated.

A disturbance resulting in sideslip will lead to a sideforce caused by the relative motion of the air over the fuselage and over the fin. There will also be a yawing moment due to sideslip, which will cause an angular velocity to develop in yaw. This will be primarily due to the influence of the fin. These effects are illustrated in Fig. 12.9. In Chapter 11 it was described how, if the wing has dihedral, the wing on the side to which the aircraft is sideslipping will experience an increase in angle of attack, and the wing on the other side a corresponding decrease. This gives rise to a rolling moment away from the direction of sideslip. This, again, is a simplification. There will be other con­tributions to the rolling moment; for example due to the fin.

A rolling moment in the opposite sense is caused by the rate of yaw men­tioned above. This time it results from the fact that one wing will be moving through the air slightly faster than the other (Fig. 12.9(a)), an effect already encountered in Chapter 11. The wing which is moving at the higher speed will have the greater lift and a rolling moment will develop as shown.

The result of all this is fairly complicated as we have a mixture of side – force, and moments in both the rolling and the yawing senses. An initial side­slip will result in a yawing motion due to the force on the fin. What happens next rather depends on whether the rolling motion caused by the sideslip and dihedral is greater than that caused by the rate of yaw and the fin. Sometimes it is not, and the resultant rolling motion means that a component of weight now acts in such a way that the sideslip is increased (Fig. 12.9(b)). The aircraft slowly diverges into a spiral path. This motion is thus called ‘spiral divergence’.

Normally the motion is fairly slow, so the aircraft is able to respond rela­tively quickly to the yawing moment and the actual degree of sideslip is small. It is easily controlled and can be removed by increasing the dihedral. However, this has an adverse effect on a second, oscillatory, lateral motion.

Fig. 12.9 Forces and moments in spiral divergence

Sideslip causes sideforce on fin in turn causing yaw, and aircraft enters a curved path. Extra velocity on outer wing causes roll leading to further sideslip and divergence. Dihedral or sweep will lead to opposite rolling moment tending to stabilise motion

As shown in Fig. 1.17, the lift coefficient is directly proportional to the angle of attack for small angles.

Figure 1.17 also shows the effect of camber on lift coefficient. It will be seen that the influences of angle of attack and camber are largely independent: that is, the increase in lift coefficient due to camber is the same at all angles of attack.

Cambered aerofoils can produce higher maximum lift coefficients than sym­metrical ones. Also, as shown in Fig. 1.17, they produce lift at zero angle of attack. The angle at which no lift is generated is therefore negative, and is known as the zero-lift angle.

The shape of the camber or mean line is important as well, as it affects the position of the line of action of the resultant lift force. Later on, we shall describe how variations in camber can be used to control the aerodynamic properties of a wing.

Figure 3.5 shows what happens when an aerofoil is rapidly accelerated from rest. At first, when virtually no lift is generated, the streamlines show an almost anti-symmetrical pattern, with a rear dividing position situated on the upper surface near the trailing edge. This pattern is similar to that given by earlier ver­sions of the classical theory, where no lift was predicted (see Fig. 1.6(b)).

As the flow speed increases, the boundary layer starts to separate at the trailing edge, due to the adverse pressure gradient, and a vortex begins to form, as shown in Fig. 3.5(b).

The vortex grows, moving rearwards, until it eventually leaves the surface and proceeds downstream, as in Fig. 3.5(c). This detached vortex is the starting vortex that we described in Chapter 2. We can see that it is the production of this starting vortex that destroys the anti-symmetry of the flow, resulting in dif­ferences in pressure and speed between the upper and lower surfaces. Thus, it is viscosity, working through the mechanism of boundary layer separation and starting vortex formation, that is ultimately responsible for the generation of lift.

The upper and lower surface flows rejoin at the trailing edge with no abrupt change of direction; the Kutta condition mentioned in Chapter 1. The upper and lower surface boundary layers join to form a wake of air moving more slowly than the surrounding air stream.

In Chapter 1 we showed how the difference in the speeds above and below the wing could be represented as being equivalent to superimposing a circulat­ing vortex type of flow on the main stream. By similar reasoning, we can say that, since the flow speed in the boundary layer is faster at the outside than at the surface, it too can be represented by a combination of rotation and translation, as illustrated in Fig. 3.6. Once again, it should be noted that no air particle actually goes round in circles. The flow in the boundary layer merely

has rotational tendency superimposed on its translational motion. However, if a speck of dust enters the boundary layer, it will rotate as it moves along.

It was mentioned above that an aircraft travelling at supersonic speed does not affect the state of the air ahead of the aircraft, while at subsonic speed the disturbance is propagated far upstream. In order to understand the reason for this we need to take a look at how the aircraft is able to make its presence felt as it travels through the air.

Figure 5.2(a) shows the nose of an aircraft flying at subsonic speed. As the flow approaches the nose of the aircraft it slows and the pressure locally increases. The influence of this region of increased pressure is transmitted upstream against the oncoming flow at the speed of sound (approximately 340 m/s at sea level). If the flow approaching the aircraft is subsonic then the disturbance will be transmitted faster than the oncoming flow and the aircraft will be able to make its presence felt infinitely far upstream.

Figure 5.2(b) shows what happens in supersonic flight. The disturbance can only make headway through an area near the nose where the flow is locally subsonic. The flow upstream is separated from this localised region by a shock wave, and is completely uninfluenced by the presence of the aircraft.

As the speed of the flow increases, so the region of subsonic flow at the nose gets smaller and the shock wave gets stronger (i. e. the pressure, density and temperature jumps all become larger).

This is why the speed of the aircraft relative to the speed of sound is the important factor in determining the flow characteristics. This ratio is known as the flight Mach number.

Flight Mach No. = Aircraft speed/speed of sound

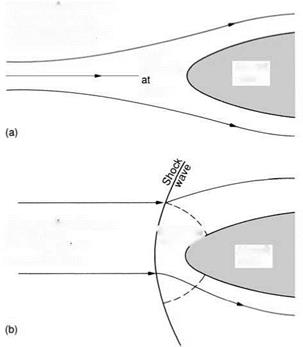Fig. 5.2 Propagation of pressure disturbances

(a) At subsonic speeds pressure disturbances generated at the nose travel at speed of sound and can make headway against oncoming flow (b) At supersonic speed the disturbances can only propagate through the locally subsonic region near the nose

When the flight Mach number is greater than one, then the aircraft is flying supersonically. When it is less than one then it is flying subsonically.

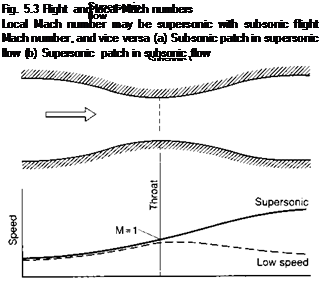
When an aircraft is flying supersonically we have seen that there may be local areas, such as the region near the nose, where the flow speed is locally reduced. Not only is the speed reduced, but the local temperature will rise, thus increasing the local speed of sound. Because of this there will be regions where the flow is locally subsonic (Fig. 5.3(a)).

Conversely, the regions on an aircraft where the flow speed is locally increased, such as the top of the wings, may lead to localised patches of super­sonic flow (Fig. 5.3(b)) even when the flight Mach number is subsonic. Thus we need to define a local Mach number for different areas of the flow.

Local Mach No. = Local flow speed/local speed of sound.

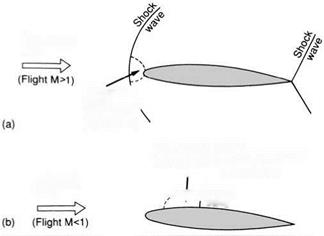Supersonic ‘patch’ due to local speeding up of flow I (Local M>1)

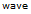
-"f’] Shock

Fig. 5.4 Change of speed along wind-tunnel duct

If there is a small pressure difference between ends of duct, speed rises to maximum at throat and then decreases

For larger pressure differences speed becomes supersonic downstream of throat

Attempts to build really large piston-engined aircraft were thwarted by the lack of power. The Bristol Brabazon (Fig. 6.16), which had eight large engines coupled in pairs through massive gearboxes to contra-rotating propellers, was a good example of the impractical result of such attempts. Imagine chang­ing the sparking plugs on that lot! It was designed to carry around a mere

Fig. 6.16 Piston-engined power The massive Bristol Brabazon 1 used eight large piston engines coupled in pairs to four sets of contra-rotating propellers. Intended as a non-stop transatlantic aerial luxury-liner, it was rendered obsolete by the faster more comfortable jet-propelled airliners. Even the turbo-prop Brabazon 2 was abandoned before completion. Piston-engined transports continued to be used for several years for freight and second-class passenger transport (Photo courtesy of British Aerospace (Bristol))

100 passengers; rather less than a typical modern small feeder-liner such as the BAe 146 (Fig. 6.26).

We saw above that the piston engine/propeller combinations give approxim­ately constant power over the typical operating speed range of the aircraft for a given fuel flow rate. Thus, as far as the engine is concerned, we will get the best endurance when operating at as low a power rating as possible. Fortunately this coincides with the airframe requirement and so we operate at the minimum power speed (Fig. 7.10).

Let us now examine further the implications for the operation of the aircraft as we did for the case of best economy. Because we are interested in low power, we need to minimise the required power not only with respect to the cruising speed, but also with respect to the cruising altitude. As we saw earlier in this chapter, the required power (equal to drag times air speed) gets greater with increasing height because of the higher air speed required for a given drag. Thus, on our simplified picture of things, we will obtain the best endurance for this type of power plant by operating at low altitude.

In order to reduce the required power still further we can use a low wing loading to reduce the speed for minimum power. Thus a piston-engined air­craft designed for endurance will tend to have a relatively large wing area.

We saw in the previous chapter that the cross-sectional area distribution of the complete aircraft was very important from the point of view of reducing the wave drag due to volume. The same is true in the transonic speed range, if the area distribution is not smooth then the transonic drag rise can be greatly increased.

Because we are concerned with Mach numbers near the speed of sound, the direction of the Mach waves in any region where the flow is supersonic will be normal to the direction of motion and so the transonic area rule is concerned with cross-sectional area normal to the centreline, unlike the supersonic case (Chapter 8).

The way in which a satisfactory distribution of cross-sectional area can be obtained varies according to the requirements of the design. In a passenger­carrying aircraft it is usually inconvenient to depart from a basically cylin­drical fuselage, and the influence of the area rule on the cross-sectional area distribution is not readily apparent unless the variation of the area along the length of the aircraft is examined in detail. In other cases, however, such as the Rockwell B1 (Fig. 9.18), the fuselage design is not restricted in this way and the influence of the area rule is clearly shown by the waisted fuselage.