Category Aircraft Flight

Air molecules are always in a state of rapid random motion. When they strike a surface, they bounce off, and in doing so, produce a force, just as you could

produce a force on a wall by throwing handfuls of pebbles against it. We describe the magnitude of pressure in terms of the force that the molecular impacts would produce per square metre (or square foot) of surface.

The air density (p) is the mass (quantity) of air in each cubic metre and the density therefore depends on how many air molecules are contained in that volume. If we increase the number of molecules in a given volume without altering their rate of movement, the force due to pressure will increase, since there will be more impacts per square metre.

The rate at which air molecules move is determined by the temperature. Raising the temperature increases the rate of molecular movement, and hence tends to increase the pressure.

It will be seen, therefore, that the air pressure is related to its density and temperature. Students of engineering may care to note that the relationship is given by the gas law p = pRT, where R is a constant.

The pressure, temperature and density of the atmospheric air all reduce significantly with increasing altitude. The variation is described more fully in Chapter 7. The reduction in density is a particularly important factor in aircraft flight, since aerodynamic forces such as lift and drag are directly related to the air density.

Highly swept wings tend to produce the stable separated conical vortex type flow described in Chapter 1, at relatively low angles of attack. For aircraft

designed to fly at twice the speed of sound or more, it becomes possible to use this type of flow for all flight conditions. On the slender-delta-winged Concorde, the leading edge was made very sharp to provoke separation even at the low angles of attack required at cruising speed. It was also warped along its length in such a way as to ensure that the vortices grew evenly along the leading edge. Figure 2.23 gives some idea of the complexity of this wing. In addition to the leading edge warp, the wing has spanwise variations in camber for reasons that will be explained later.

The conical leading edge vortices extend downstream, and the usual trailing vortices are formed, as illustrated in Fig. 1.21. One advantage of this type of flow is that tip stalling does not occur, since the flow is already separated and stable.

From the plan view of Fig. 2.24 it will be seen that the wings of Concorde were not a true delta, but had curved leading edges; a shape that is known as an ogive. The ogive shape has the effect of moving the position of centre of lift rearwards and also reduces the variation of the position of the centre of lift with angle of attack and speed.

Concorde was originally envisaged as flying with conventional attached flow in cruise, but it was found that the optimum cruise condition was obtained with a small amount of leading edge vortex flow.

Highly swept wing root strakes are used on some aircraft to provide a com­bination of separated conical vortex flow inboard, and conventional flow outboard. Wing root strakes may be seen on the F-18 in Fig. 2.25. With this arrangement, at high angles of attack, the loss of lift on the outboard wing sections may be more than compensated for by the extra conical vortex-lift generated by the strakes. The vortex produced by the strakes also helps main­tain flow attachment on the wing, as described in Chapter 3.

Another way of increasing the proportion of laminar boundary layer on a wing of given area, is to reduce the chord of the section, while increasing the wing span: in other words, by increasing the aspect ratio. Thus, high-aspect-ratio wings can be beneficial in reducing both trailing vortex and surface-friction drag.

Artificially induced laminar flow

In order to preserve a low-drag laminar boundary layer over an even larger proportion of the surface of an aircraft, the engines can be used to provide suction to remove the boundary layer through slots, as described in the previ­ous chapter, or through a porous skin. Several research aircraft have been flown with experimental porous or slotted surfaces. A good description of early postwar experiments is given by Lachmann (1961). Although very low drag values were often obtained, it was discovered that there were consider­able practical difficulties, particularly in keeping the holes free of debris and suicidal insects. A boundary layer suction system would increase the cost, complexity and weight of the aircraft. The engine performance, and the air­craft handling properties may also be adversely affected. Thus far, there has been no widespread application of suction-induced laminar flow in production aircraft.

For many years, the main concession to the idea of using engine suction in this way, has been the occasional use of a pusher propeller situated at the rear of the fuselage or engine nacelle, as in the Beech Starship shown in Fig. 4.10. The rear-mounted propellers ensure that there is a favourable

Fig. 4.10 Vertical surfaces on the wing tips of the canard-configuration Beech Starship combined the functions of drag-reducing winglet and fin (Photo courtesy of Beech Aircraft Corp.)

pressure gradient (air moving towards a lower pressure) over the nacelles, and a large area of the wing. This in turn delays the transition to a turbulent flow, and inhibits separation. Proponents of the aft-mounted pusher propeller claim considerable reductions in drag by this method, but this may be partially offset by a deterioration in propeller efficiency. A more significant advantage of this arrangement is the reduction in cabin noise.

As with wings, increasing the aspect ratio of the propeller blades reduces the drag or resistance. However, the amount of thrust that can be produced, depends on the total blade area, so the use of high aspect ratio blades may result in an unacceptably large propeller diameter. Large high-powered propeller-driven aircraft often have low-aspect-ratio ‘paddle’ blades.

A small number of blades is preferable as it reduces the mutual interfer­ence effect between blades. However, maintaining sufficient total blade area to transmit the required power through a given diameter may necessitate a compromise between aspect ratio and number of blades. The Spitfire, which started life with only two blades and 1000 bhp, ended up as the Seafire 47 with six blades (on two co-axial contra-rotating propellers) and 2350 bhp. The diameter was limited by ground clearance. The Lockheed Super Hercules, shown in Fig. 6.6 uses high-aspect-ratio six-bladed 4.11 m diameter propellers.

Increasing the number of blades also reduces the amount of thrust that has to be produced by each blade, which is an advantage in high speed operation, as it lowers the maximum local Mach number on the blades. The importance of limiting the Mach number is described later.

In Chapter 1 it was shown that the lift developed by the wings of an aircraft must be equal to the weight at all times for steady horizontal flight. This is also approximately true for a steady climb, provided the angle of climb is not excessive.

As the speed is reduced, the lift is kept constant by increasing the angle of attack of the wings by using the elevators to raise the nose of the aircraft, as described in Chapter 10. In order for the new speed to be maintained, the drag of the aircraft must be exactly balanced by the engine thrust and so, in general, the throttle will need to be adjusted to bring this about.

We saw in Chapter 4 how the vortex drag, the surface friction and bound­ary layer pressure drag of an aircraft flying straight and level combined to give the typical variation shown in Fig. 7.4.

It is important in understanding the graph to remember that the wing angle of attack has been adjusted to give the same total lift at each speed. The most important feature to notice is the fact that the drag has a minimum value at a particular speed; the minimum drag speed.

Normally the aircraft will be operated at a speed greater than the speed corresponding to the minimum drag value, and a change in speed may, for example, result in the operating point on the graph moving from A to B in Fig. 7.4. The increase in drag will normally mean that the engine setting will have to be changed to produce the required extra thrust.

We can get a better picture if we also plot a series of curves showing how the engine thrust varies with speed for a number of different throttle settings. In Fig. 7.4, curves for a typical turbo-jet, at constant altitude, are shown. How­ever, exactly the same argument can be used whatever the powerplant. The steady flight ‘operating point’ for the aircraft occurs at the position where the drag and thrust curves intersect (i. e. when thrust=drag), and inspection of the intersection at points A and B shows that a higher throttle setting is required at B.

So far this feels right intuitively. If we want to go faster we increase the throttle setting and put the nose down to reduce the angle of attack as the speed increases. This simple view can, however, be misleading. In many cases the operating point will be quite close to the minimum drag point, say at point C in Fig. 7.4. A change in speed will thus lead to a relatively small change in the drag of the airframe as we move to point D. Further, the change in thrust with forward speed for a turbo-jet is frequently not very great. The net result of all this is that the required change in throttle setting may, in practice, be small, even for quite a substantial speed change. In this case it is primarily the change in angle of attack, produced by the change in elevator setting, which alters the speed.

This point is discussed further in Chapter 10, where we see that trying to operate below the minimum drag speed can lead to an unstable situation.

At hypersonic speed it is possible to use a somewhat different method to produce lift. An example of this type of configuration is the so-called ‘caret wing’ (Fig. 8.21). In this, as in all similar configurations, the top surface is

aligned with the air stream so that it does not provide any contribution to the lift. The wing has supersonic leading edges at the hypersonic cruise Mach number and the shock wave generated by the lower surface is trapped within the leading edges. The pressure increase behind the shock wave generates the required lift.

Other configurations use the shock wave generated by the fuselage, rather than a thick wing; this shock wave being similarly ‘trapped’ by the wing. An example of this is shown in Fig. 8.22. Such configurations provide poten­tially acceptable lift/drag ratios at hypersonic speed. They have the additional advantage that their aerodynamic characteristics will be acceptable throughout the supersonic and subsonic speed ranges as they are effectively slender delta wings.

pressure

Fig. 8.23 Surface fuel burning

Schematic arrangement of a proposed wave-rider aircraft

The air is compressed through a series of shock waves. Fuel is injected and burned as in a ramjet. The heated exhaust is at a relatively high pressure, and acts on the lower rear surface of the wing to produce components of lift and thrust

It is interesting to observe that these configurations feature either blunt wing trailing edges, blunt fuselage bases, or both. At subsonic speeds such features are very bad from the point of view of drag production. With the wave-rider it is, however, difficult to design suitable ‘shock capturing’ geometries which do not exhibit these features. Fortunately the base drag produced is of much smaller significance.

In any event the blunt base provides a convenient site for the engines and by ejecting hot exhaust gases from the base we can eliminate the drag contribution from this region. This is another example of an integrated aircraft where the propulsive system forms part of the aircraft aerodynamic system.

High Mach number flight opens up a number of interesting propulsion possibilities. Because of the compression produced by the shock waves, fuel can be directly injected into the air stream and burned, effectively producing an external ramjet (Fig. 8.23). It is possible to do this, not only on the base of the aircraft but also on the lifting surfaces thus producing an integrated lift/propulsion system.

It must, though, be remembered that such a device will cease to work at low speed and alternative means of propulsion will be necessary with associated performance penalties due to increased weight.

One problem with power-operated controls is that the pilot has no direct feel for the amount of force that the control surface is producing. Therefore, some form of artificial feel has to be introduced.

Generally, mechanical controls feel heavier the further they are pulled, so a crude form of feel could be provided by attaching springs to the control column. This system is inadequate, however, because the control loads should also increase as the flight speed increases.

The force actually required at the control surface, depends on the dynamic pressure (-pV2), rather than just the speed. At constant altitude, the controls will, for example, require sixteen times more force to operate them at 800 km/h than at 200 km/h. To overcome this problem, a so-called q-feel device can be added. (q is the symbol conventionally used to denote dynamic pressure.) The q-feel unit is a device which is attached to the mechanical control linkage to increase its stiffness in proportion to increases in dynamic pressure. Nowadays, much more sophisticated feedback systems are used, in which the force required to move the control surface is sensed, and the force required to move the pilot’s control stick is increased appropriately.

By using electronic processing of the feedback signal, it is possible to make a small aircraft feel and handle like a large one. Reversing the procedure might be unwise, as trying to throw a 747 around like a Pitts Special could cause problems. The handling of new untested aircraft types is often simulated by artificially modifying the controls of an existing different aircraft type.

The two ‘lateral’ motions which we have so far discussed have not been oscillatory in nature. The first was a heavily damped motion which takes place almost entirely in roll and the second, the spiral mode, primarily involves motions in yaw and sideslip. A third motion also occurs which takes the form of an oscillation.

This motion mainly consists of a combination of roll and yaw and the result is rather similar to a boat crossing a choppy sea obliquely to the waves. It has acquired the somewhat libellous name of ‘Dutch roll’ because of the supposed resemblance to the motion of a drunken Dutch sailor. The authors dissociate themselves entirely from any suggestion that Dutch sailors are more prone to intoxication than those of other nations, or that, when intoxicated, their gait is peculiarly eccentric!

Because the motion involved in Dutch roll is particularly unpleasant to the occupants of the aircraft, steps are usually taken to ‘design it out’ as far as possible, even though this usually means that some degree of spiral instability results.

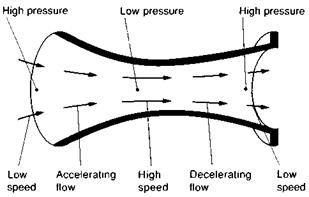
The way in which the motion develops is as follows. If the aircraft is dis­turbed in the yawing sense then the fin will provide the restoring moment, known as ‘weathercock stability’, which will bring the aircraft back to its original heading. There will be an overshoot, however, and the aircraft will oscillate about its equilibrium position (Fig. 12.10). At the point of overshoot there will be an additional force on the fin due to the angular velocity in yaw (Fig. 12.10) and this will tend to oppose the motion and damp out the oscillations.

The motion is much more complicated than this, though, because during the period when the aircraft is yawed a rolling moment will be caused by the dihedral and sweep effects, as we have seen previously. This rolling moment will be maximum at the maximum angle of yaw (Fig. 12.11). There will also be a rolling moment due to the rate of yaw because one wing is travelling through the air at a higher speed than the other. Unlike the spiral mode, this tends to reinforce the rolling moment due to dihedral and sweep. However it will have its maximum value when the yawing velocity, rather than angle, is at its greatest. The motion is therefore a complicated mixture of rolling and yawing. No wonder it is so unpleasant!

The rolling motion will also react back on the motion in yaw. When the air­craft is rolled there will be a weight component inducing sideslip. This sideslip velocity will reduce the damping moment provided by the fin as the aircraft passes through the equilibrium position (Fig. 12.12). Thus the effect of dihed­ral or sweep, both of which encourage roll, is to reduce the damping of the motion. They also cause a slight reduction in the frequency of the oscillation.

Typically the motion has a period of a few seconds. For straight-wing air­craft the damping is usually quite good, but for swept-wing aircraft it can cause more of a problem, because the sweep accentuates the rolling and sideslip.

Air stream

Yawing displacement causes fin force tending to restore aircraft to its original attitude

LL >

As aircraft passes through its original position

yawing velocity is maximum. Resulting fin force opposes the motion, tending to damp oscillation

Fig. 12.10 Effect of fin in Dutch roll

Unfortunately, when we considered the spiral instability we found that increas­ing dihedral had the effect of improving the stability. Thus, if we decrease dihed­ral to improve damping in Dutch roll we make the spiral divergence worse. Usually a small degree of spiral instability is tolerated in order to alleviate the less pleasant Dutch roll.

In steady level flight, the lift force must always be equal and opposite to the aircraft weight. In landing and take-off where the speed, and thus dynamic pressure, are low, a large CL value is required. As the flight speed increases, the lift coefficient required reduces.

The pilot controls the lift coefficient value primarily by altering the angle of attack of the aircraft. The angle of attack must be gradually reduced as the flight speed increases. Most aircraft are designed to fly in a near level attitude at cruise, and must therefore adopt a nose-up attitude on landing and take-off. An extreme example was Concorde, as illustrated in Fig. 1.20. On landing, the angle of attack of this aircraft was so large, that the nose had to be hinged downwards, otherwise the pilot would not have been able to see the runway.

Airliners cruise at high altitude, where the air density is much lower than at sea level. The reduction of density p, which reduces the dynamic pressure, partly compensates for the difference between the cruising and landing speeds. The maximum CL required at take-off, however, may still be many times greater than the minimum cruise value.

Very early aircraft such as that shown in Fig. 1.7(a) could only just stagger into the air, and their maximum speed was little greater than their take-off speed. As seen in Fig. 1.7(a), such aircraft therefore had a highly cambered wing section that produced a large CL in order to minimise the wing area and hence keep the weight down. Most modern aircraft have a less cambered wing section that is optimised to produce low drag at cruising speed. The high lift coefficient required for landing is normally produced by means of some form of flap which effectively increases the camber and sometimes the area of the wing (see Fig. 3.13). Flaps and other high lift devices are described in Chapter 3.

Since the type of boundary layer influences both surface friction drag and flow separation, it is important to know what factors control the transition from laminar to turbulent boundary layer flow.

We have already mentioned that if the pressure is decreasing in the direction of flow (a favourable pressure gradient) transition is delayed. Transition is also delayed if the surface is smooth and without undulations.

The position of transition to turbulent flow on an aerofoil moves forwards with increasing speed V and also if the air density p is increased. It moves rear­wards if the coefficient of viscosity R (a measure of the stickiness) increases. The distance of the transition from the leading edge also depends on the aero­foil chord length c for a given section shape, since increasing the chord, and hence the overall size, will increase the length of the region of favourable pres­sure gradient.

The dependence of the transition position on the speed, density viscosity and chord, as described above, can be expressed in terms of a single quantity known as the wing Reynolds number, where

density x speed x wing chord

Wing Reynolds number is

viscosity coefficient

or in mathematical symbols

Re = (PVC)

R

The transition position moves forward as the Reynolds number increases.

Reynolds number is just a number with no dimensions, like a ratio. It is a term that frequently crops up in aerodynamic literature, and always has the form (pVl)/R where l is a length.