5.2.2.1 Steady heading sideslips
The control deflections required to maintain an unaugmented helicopter in a steady sideslip are related to its lateral and directional static stabilities. In a steady sideslip the rates of roll and yaw will be zero, therefore the rolling and yawing aerodynamic moments must have been balanced by control deflections generating control moments. The linearized form of the lateral/directional equations of motion for a helicopter, with the centre of gravity situated at the body axes origin, can be written as follows:
m[rUe + v – pWe ] = Yv. v + Yp . p + Yr. r + mgф cos 6e + YA, . A, + Y0tr. 6tr
Ixxp – Ixzr = Lv. v + Lp. p + Lr. r + LM. A, + L0tr. 6tr
Izzr – Ixzp = Nv. v + Np. p + Nr. r + NA, . A, + N0tr. 6tr
Now when performing a SHSS the pilot endeavours to achieve the off-trim condition by co-ordinated movement of both the lateral cyclic and the yaw pedals without developing any sustained pitch, roll or yaw rate. Once ‘on-condition’ the lateral velocity will be constant, indicated by a fixed sideslip angle. So:
v = p = Г = p = r = 0
Thus the equations of motion reduce to:
0 = Yv. v + mgф cos 0e + YA,. A, + Y. tr. 0tr
0 = Lv. v + [8]a,. Ai + L0tr. 0tr
0 = Nv. v + Na, . A, + N0tr. 0tr
If it is assumed that the roll attitude remains small, such that ф в 0, then:
0 = Yv. v + YA,. A, + Y0tr. 0tr
0 = Lv. v + LA, . A, + L0tr. 0tr
0 = Nv. v + Na, . A, + N0tr. 0tr which leads to:
0 = v(Yv. L0tr – Y0tr. Lv) + A,(YA,. L0tr – Y0tr. LA,)
A, = (Yv. L0tr – Y0tr. Lv) v (Y0tr. lm – ym . L0tr)
If the rolling moment due to tail rotor collective (pedal) is negligible, such that L0tr = 0, then:
A = -_L_ v La,
also:
0 = v(Yv. NAl – YAl. Nv) + 0tr (F0tr. NAl – YAl. N0„)
0tr (Yv. NAl – YAi. Nv)
v = (YAl. N0tr – Y0tr. NAl)
If the yawing moment due to lateral cyclic is negligible, such that NAl = 0, then:
0Г = – N
v N0tr
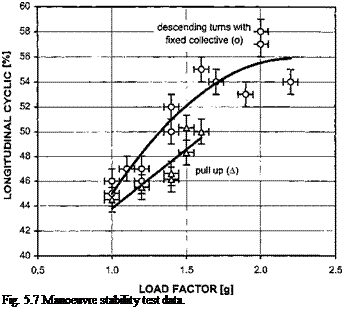
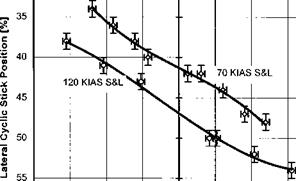
For positive lateral static stability, the slope of the control deflection versus sideslip graph will be negative. That is, in order to increase sideslip to starboard the pilot must apply an increased right lateral cyclic stick deflection. For positive directional static stability, the slope of the pedal deflection versus sideslip graph will be positive. That is, in order to increase sideslip to starboard the pilot must apply increased left pedal. Note that in each case the magnitude of the control deflection required to maintain a given sideslip angle depends, on the degree of stability and the amount of control power. Useful techniques to determine the relationship between stability and control power are turns on one control (TO1C) which are described later.
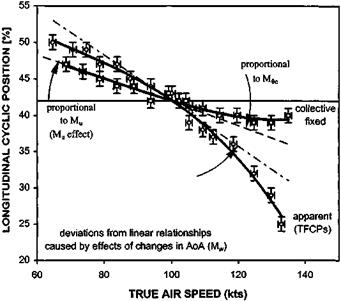
As PEs are often present in sideslipping flight the test technique consists of stabilizing in a steady heading sideslip at constant EAS, recording roll attitude, lateral cyclic and yaw pedal positions. It should be noted that steady heading sideslip (SHSS) tests will only indicate the amount of control displacement required to counter the rolling and yawing moments generated by the sideslip. The amount of control displacement should increase as lateral velocity increases and for stability should be in the same direction as the sideslip for lateral cyclic and in opposition for the yaw pedals. Whether, for example, a small control displacement is due to weak stability or high control power must be determined by some other test technique such as turns on one control, which are described later. Figures 5.5 and 5.6 illustrate the presentation of typical results. From these plots it can be seen that at each speed the control movement is in the correct sense and that increasing control deflection is required for increasing lateral velocity.
Tests are normally made in level flight at the minimum power speed, VNE – 20 kts and one intermediate speed. In climbing and autorotative flight the speed will normally be the recommended climbing speed and the speed for minimum rate of descent in autorotation respectively. If no sideslip angle indicator is fitted an approximation of sideslip can be obtained by employing one of the methods described below: 1 [9]
зо
|
LEFT
RIGHT
|
60 ————————————————————————————————
-40 -30 -20 -10 0 10 20 30 40
LEFT Lateral Velocity (v) [kts] RIGHT
Fig. 5.5 SHSS test data – lateral static stability.
|
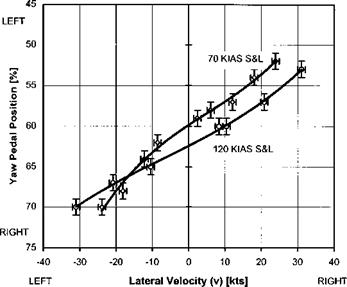
Fig. 5.6 SHSS test data – directional static stability.
|
Note the actual heading change when established in a steady-state condition and this approximates to the sideslip angle.
An approximate ‘calibration’ of slip-ball displacement to sideslip angle can also be obtained during either of the above techniques. Also, if a suitable line feature is
selected and there is no wind (or very light wind down the line feature) it may be possible to estimate inherent sideslip by noting the line feature heading and then comparing this to the heading required to track down the line feature with wings level and ball centred. The difference between the line feature heading and the heading required to track the line feature will equate to the inherent sideslip value for the test airspeed.
Before starting, the ASI PECs with sideslip are obtained for the test speeds. This is particularly important at high IAS to avoid exceeding VNE. Steady sideslips are flown at constant EAS to eliminate inconsistencies due to pressure errors at high angles of sideslip. If ASI PECs with sideslip are not available, it should be possible to obtain satisfactory steady sideslip results by using the following method:
(1) Stabilize the aircraft wings level with inherent sideslip (ball centred) at the IAS which gives the EAS for the test condition.
(2) Smoothly but rapidly yaw the aircraft to the required sideslip angle controlling the bank with lateral cyclic to maintain a SHSS, and note the new IAS immediately.
(3) Maintain this IAS and record the test parameters.
(4) Yaw the aircraft smartly back to wings level and the inherent sideslip value (ball centred) and note that the IAS returns to the original value.