Category MECHANICS. OF FLIGHT

What are the possibilities of reducing this minimum velocity of flight?

In all forms of transport, with the exception of flying, the maximum speed attainable is a major consideration. But in the exceptional case of flight it is equally important to obtain a low minimum speed as it is to obtain a high maximum speed. This low speed is of such importance that it is apt to be exag­gerated at the expense of the maximum speed. Whatever we say about obtaining a low landing speed, we must never forget that the chief advantage of flight over other means of transport depends on the high speed obtainable. But, provided we bear this in mind, everything must be done to reduce the landing (and taking off) speed, because only in this way can flying be made a popular and safe means of transport. The minimum speed of most light aero­planes is as much as 50 or 60 knots, and of some more than 100 knots.

Much of what has been said applies not only to level flight, but to stalls when gliding, climbing or turning; for instance, when banking on a turn the lift on the wings must be greater than the weight, and therefore the stalling speed is higher than when landing. Also at height the air density p will be less, and this means that in order to keep CL. тpV. S equal to the weight, the stalling speed V will be greater than at ground level. Fortunately the air speed indicator, which is in itself worked by the effect of the air density, will record the same speed when the aeroplane stalls as it did at ground level; in other words, the indicated stalling speeds will remain the same at all heights.

But on high airfields, such as are found in mountainous countries, the true landing speed of an aeroplane will be appreciably higher than on sea-level air­fields; and in tropical countries the air density is decreased owing to the high temperatures, and the true landing speed is consequently increased. The taking-off speed, and the run required, are also increased in both these instances, and this is perhaps an even more important consideration.

When stalling intentionally the aeroplane is pulled into a steeply climbing attitude and the air speed allowed to drop to practically nil until the nose sud­denly drops or, as frequently happens, one wing drops and the aeroplane commences to dive or spin.

Before leaving the subject of stalling it might be as well to mention that there has always been difficulty in deciding upon an exact definition of stalling or stalling speed. The stall occurs because the smooth airflow over the wing becomes separated – but this is a gradual process. At quite small angles of attack there is some turbulence near the trailing edge; as the angle increases, the turbulence spreads forward. What is even more important is that it also spreads spanwise, usually from tip to root on highly-tapered wings, and from root to tip on rectangular wings. If we define the stall as being the break up of the airflow, when did it occur? There may be buffeting of the tail plane or main planes, but this too may be slight and unimportant, or it may be violent. As a result of the change from smooth to turbulent airflow the curve of lift coeffi­cient reaches a maximum and then starts to fall. We defined the stalling angle in Chapter 3 as the angle at which the lift coefficient is a maximum. But how does the pilot know that it is at its maximum value? All the pilot knows is that if he tried to fly below a certain speed he gets into difficulties. How great the difficulties depends on the type of aircraft, and the extent to which the pilot can overcome them depends on a lot of things, but particularly on his own skill.

In fact, there are different definitions of stalling according to the point of view of the person who wishes to define it – the pilot looks at it one way, the aerodynamicist another, and so on. What is important is that each should realise that it is his own definition, and that all these things do not necessarily occur at the same time.

The art of landing an aeroplane consists of bringing it in contact with the ground at the lowest possible vertical velocity and, at the same time, some­where near the lowest possible horizontal velocity relative to the ground. It is true that in certain circumstances a fast landing may be permissible, and that some modern aircraft are flown onto the ground in a definitely unstalled con-

(a)

(g)

Fig 6.5 Air brakes dition, but the general rule applies to the landings of many slower and lighter types, and especially to forced landings in which everything usually depends on the minimum horizontal velocity being achieved.

The reader will have noticed that it is the horizontal velocity relative to the ground which must be reasonably low. Now, the first step in this direction is to land against the wind and so reduce the ground speed. This, however, is entirely up to the pilot; in our present problem we are only concerned with a low air speed. Given this low air speed, the pilot can, by landing into the wind obtain a low ground speed. In the case of landing on the decks of ships (Fig. 6B, overleaf), if the ship herself steams into the wind, the ground speed will be still further reduced. Supposing, for instance, the minimum air speed of an aeroplane is 80 knots, the wind speed is 20 knots, and the ship is steaming at 30 knots into the wind, then the ‘ground’ speed of the aeroplane when landing will be only 30 knots; while if the wind speed had been 50 knots, the ‘ground’ speed would have been reduced to nil – a perfectly possible state of affairs.

In an early chapter it was mentioned that the wind speed is apt to be irreg­ular near the ground, and it is when landing that such irregularity may be important. If the wind speed suddenly decreases, the aircraft, owing to its inertia, will tend to continue at the same ground speed and will therefore lose air speed, and, if already flying near the critical speed, may stall. Similarly, if the wind speed suddenly increases, the aircraft will temporarily gain air speed and will ‘balloon’ upwards, making it difficult to make contact with the ground at the right moment. Such instances may occur in changeable and gusty winds, in up-currents caused by heating of parts of the earth’s surface, in cases of turbulence caused by the wind flowing over obstructions such as hills and hangars, and due to wind gradient. Of these, wind gradient is prob­ably the most important, and the most easily allowed for. An aeroplane, when landing against a high wind, will encounter a decreasing wind speed as it descends through the last few feet and will be in danger of stalling unless it has speed in hand to compensate for the air speed lost. If landing up a slope or towards a hangar, one may suddenly run into air which is blanketed by the

Fig 6B Deck landing

(By courtesy of the former British Aircraft Corporation, Preston) The Jaguar, designed by Breguet and ВАС, landing on a deck.

obstruction, or a head wind may even become a following wind blowing up the hill or towards the hangar. In a really high wind, and when flying a small light aircraft, these conditions may be dangerous, and the obvious moral is to allow for them by approaching to land at a higher speed than usual.

The vertical velocity of landing can be reduced to practically nothing pro­vided the forward velocity is sufficient to keep the aeroplane in horizontal flight – that is to say, provided the lift of the wings is sufficient to balance the weight of the aeroplane.

We have already seen that there is a definite relationship between the indi­cated air speed and the angle of attack. Fig. 6.6 illustrates the attitudes of an aeroplane at various speeds and the corresponding angles of attack required to maintain level flight: (a) shows the attitude of maximum speed; (b) that of normal cruising flight; (c) that for an ordinary landing; and (d) the attitude when fitted with flaps and slots and flying as slowly as possible.

Now, since lift must equal weight, and must also equal CL. ypV2 . S, it is quite obvious that if У is to be as small as possible, CL must be as large as poss­ible. The pilot may never have heard of a lift coefficient, and he may be none the worse a pilot for that; but, consciously or unconsciously, he will increase CL by increasing the angle of attack until he decides (it matters not whether his decision is based on scientific knowledge, instinct or bitter experience!) that

Fig 6.6 Attitudes for level flight

any further increase in the angle of attack will decrease rather than increase the lift; in other words, until he has come near to that stalling angle which we considered so fully when dealing with aerofoils. At this angle (about 15° to 20° in the case of an ordinary aerofoil), CL is at its maximum, and therefore V is a minimum.

If the pilot, through lack of any of the three qualities mentioned above, exceeds this angle, then both CL and V will decrease; therefore CL. ypV2 . S can no longer equal the weight and the aeroplane will commence to drop. For 20 m, 50 m, or more, the vertical component of velocity will increase and the nose of the aeroplane will drop, therefore the pilot must beware that, when he does this experiment of flying as slowly as possible, he is either very near the

ground or at a considerable height above it. In fact, slow landings should not be practised between 1 and 500 m from the earth’s surface, and the whole skill of the pilot is exercised in approaching the ground in such a manner that he has reached the correct condition of affairs just as he skims the surface of the runway, provided, of course, that he has sufficient clear run in front in which to pull up after landing.

It should not be thought that a flat gliding angle is always an advantage; when approaching a small airfield near the edge of which are high obstacles, it is

Fig 6A Gliding

(By courtesy of Slingsby Sailplanes Ltd)

The Skylark 4 with large aspect ratio and good value of lift/drag; needing spoilers to increase gliding angle when necessary.

advisable to reach the ground as soon as possible after passing over such obstacles. In these circumstances a flat gliding angle is a definite disadvantage, and even if the aeroplane is dived steeply it will pick up speed and will tend to float across the airfield before touching the ground.

The gliding angle can be steepened by reducing the ratio of lift to drag; this can be done by decreasing the angle of attack (resulting in too high a speed), or by increasing the angle of attack (resulting in an air speed which may be too low for safety), or by using an air brake (Fig. 6.5). The last is by far the most satisfactory means, and the air brake may take the form of some kind of flap, such as was described in the chapter on aerofoils; but the modern tendency is to use the various types of flap when lift is required, and separate air brakes or spoilers when drag is required.

The conclusion of the previous paragraph might perhaps lead one to ask whether, in that case, there is any need for a sailplane to be built of light con­struction. The answer is definitely – Yes. A sailplane (Fig. 6A, overleaf) must have a flat gliding angle if it is to get any distance, any range from its starting point; but, even more important, it must have a low rate of vertical descent or sinking speed; it must be able to stay a long time in the air and be able to take advantage of every breath of rising air, however slight. Sailplane pilots do sometimes add ballast so as to increase the flight speed as this can be useful under certain circumstances. However, a description of such advanced sailplane techniques is best left to books devoted specifically to that subject. It is easy to see that the rate of vertical descent depends both on the angle of glide and on the air speed during the glide. Therefore to get a low rate of descent we need a good lift/drag ratio, i. e. good aerodynamic design, and a low air speed, i. e. low weight.

Actually we shall get a lower rate of descent by reducing speed below that which gives the flattest glide; this is because we gain more by the lower air speed than we lose by the steeper glide. Thus there is an ‘endurance’ speed for gliding just as for level flight and, as before, it is lower than the range speed, and corresponds to the speed for minimum power requirement.

It is commonly thought that heavy aeroplanes should glide more steeply that light aeroplanes, but a moment’s reflection will make one realise that this is not so, since the gliding angle depends on the ratio of lift to drag, which is quite independent of the weight. Neither in principle nor in fact does weight have an appreciable influ­ence on the gliding angle, but what it does affect is the air speed during the glide.

Look back for a moment at Fig. 6.1. Imagine an increase in the line repre­senting the weight; there will need to be a corresponding increase in the total aerodynamic force, and a greater lift and a greater drag. But the proportions will all remain exactly the same, the same lift/drag ratio, the same gliding angle. But the greater lift, and greater drag, can only be got by greater speed. If we now think back to flying for range, it will be remembered that the con­dition was the same: greater weight meant greater speed. But there is an interesting and important difference in this case. In flying for range, greater speed meant greater drag, greater thrust, and so less range. In gliding without engine power, greater speed means greater drag, but now the ‘thrust’ is pro­vided by the component of the weight which acts along the gliding path and this, of course, is automatically greater because the weight is greater. So greater weight does not affect the gliding angle and does not affect the range, on a pure glide – but it does affect the speed.

Tet us remember once again that gliding must be considered as relative to the air. To an observer on the ground an aeroplane gliding into the wind may appear to remain still or, in some cases, even to ascend. In such instances there must be a wind blowing which has both a horizontal and an upward velocity, and to an observer travelling on this wind in a balloon the aeroplane would appear to be travelling forwards and descending. When viewed from the ground an aeroplane gliding against the wind will appear to glide more steeply, and will, in fact, glide more steeply relative to the ground (Fig. 6.4); and when gliding with the wind it will glide less steeply than the real angle measured rela­tive to the air – the angle as it would appear to an observer in a free balloon.

(a) Slow glide at slope of 1 in 8 (7°). Angle of attack 13°. Speed 115 knots.

(b) Fast glide at slope of 1 in 8 (7°). Angle of attack 1 f°. Speed 210 knots.

(c) Flattest glide at slope of 1 in 12 (5°). Angle of attack 4°. Speed 155 knots.

Note. In the diagram the gliding angles, and the differences between them, have been exaggerated so as to bring out the principles.

Angle of attack

Fig 6.3 Lift/drag curve and gliding angles of aeroplane

v

Fig 6.4 Effect of wind on angle of glide relative to the earth

By a process of simple geometry, it is easy to see that the angle formed between the lift and the total aerodynamic force is the same as the angle a between the path of the glide and the horizontal, which is called the gliding angle. Therefore

D/L = tan a

This means that the less lower value of D/L – i. e. the greater the value of L/D – the flatter will be the gliding angle.

From this simple fact we can very easily come to some important conclu­sions; for instance –

1. The tangent of the gliding angle is directly dependent on the L/D, which is really the ‘efficiency’ of the design of the aeroplane, and therefore the more ‘efficient’ the aeroplane, the farther it will glide, or, expressing it the other way round, the measurement of the angle of glide will give a simple estimate of the efficiency of the aeroplane.

The word ‘efficiency’ is apt to have a rather vague meaning, and we are using it here in a particular sense. We are concerned only with the success or otherwise of the designer in obtaining the maximum amount of lift with the minimum of drag, or what might be called the ‘aerodynamic’ merit of the aeroplane. For instance, our conclusion shows that any improvement which reduces the drag will result in a flatter gliding angle.

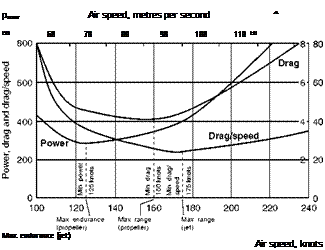
It will be noticed that this is the same criterion as for maximum range, so that an aeroplane that has a flat gliding angle should also be efficient at flying for range, neglecting the influence of the propulsion efficiency.

2. If an aeroplane is to glide as far as possible, the angle of attack during the glide must be such that the lift/drag is a maximum.

The aeroplane is so constructed that the riggers’ angle of incidence is a small angle of, say, 2° or 3°. This particular angle is chosen because it is the most suitable for level flight. As was explained when considering the characteristics of aerofoils, the modern tendency is to make this angle rather less than the angle of maximum L/D (because we are out for speed), but, even so, it will be within a degree or so of that angle, so it is true to say that the angle of attack during a flat glide will be very nearly the same as that during straight and level flight, and almost exactly the same as when flying for maximum range with piston engines.

The pilot finds it fairly easy to maintain ordinary horizontal flight at the most efficient angle because the fuselage is then in a more or less hori­zontal position. When gliding however, the task is not always so easy. Sophisticated modem aircraft may be fitted with an angle of attack indi­cator, but on older and simpler types this is not normally the case. Fortunately, as in level flight, there is a direct connection between the air speed and the angle of attack, and therefore the air speed can be found which gives the best gliding angle, and this acts as a guide to the pilot. The fact remains, however, that it requires considerable skill, instinct, or what­ever one likes to call it, on the part of a pilot to glide at the flattest possible angle. This is the type of skill which is especially needed by the pilot of a motorless glider or sailplane.

It should be noted that, although there is a relationship between air speed and angle of attack on the glide just as there is in level flight, the relation­ship is not exactly the same, and the speed that gives the flattest gliding angle is usually rather less than the speed that gives maximum range. The difference, however, is small and the principle is the same.

3. If the pilot attempts to glide at an angle of attack either greater or less than that which gives the best L/D, then in each case the path of descent will be steeper.

Perhaps this conclusion may be considered redundant because it is simply another way of expressing the preceding one. It is purposely repeated in this form because there seems to be such a strong natural instinct on the part of pilots to think that if the aeroplane is put in a more horizontal atti­tude it will glide farther. Even if one has never flown it is not difficult to imagine the feelings of a pilot whose engine has failed, and who is trying to reach a certain field in which to make a forced landing. It gradually dawns on him that in the way in which he is gliding he will not reach that field. What, then, could be more natural than that he should pull up the nose of his aeroplane in his efforts to reach it? What happens? In answer to this question the student often says that he will stall the aeroplane. Not necessarily. He should in the first place have been gliding nowhere near the stalling angle, but at an angle of attack of only about 3° or 4°, so that he has many degrees through which to increase the angle before stalling. But what will most certainly happen is that the increase in angle will decrease the value of L/D and so increase the gliding angle, and although the aero­plane will lie flatter to the horizontal, it will glide towards the earth at a steeper angle and will not reach even so far as it would otherwise have done. The air speed during such a glide will be less than that which gives the best gliding angle.

Suppose, on the other hand, that, when a pilot is gliding at the angle of attack which gives him the greatest value of L/D, he puts the nose of the aeroplane down, this will decrease the angle of attack which, as before, will decrease the value of L/D and therefore increase the steepness of the gliding path, the air speed this time being greater than that which gives the best gliding angle.

It is not easy to visualise the angle of attack during a glide, and the reader, like the pilot, must be careful not to be confused between the direction in which the aeroplane is pointing and the direction in which it is travelling. It is hoped that the figures may help to make this important point clear (Figs 6.2 and 6.3, overleaf).

In the previous chapter we discovered that the ratio of lift to drag of complete aeroplanes may be in the neighbourhood of 8, 10 or 12 to 1. These values cor­respond to gliding angles of which the tangents are 1/8, 1/10 and 1/12, i. e. approximately 7°, 6° and 5° respectively. Thus, neglecting the effect of wind, a pilot will usually be in error on the right side if he assumes that he can glide a kilometre for every 200 metres of height, i. e. if he reckons on a gliding angle of which the tangent is 1/5.

Gliding

Let us next consider the flight of an aeroplane while gliding under the influ­ence of the force of gravity and without the use of the engine.

Of the four forces, we are now deprived of the thrust, and therefore when the aeroplane is travelling in a steady glide it must be kept in a state of equi­librium by the lift, drag, and weight only. This means that the total aerodynamic force – that is to say, the resultant of the lift and drag – must be exactly equal and opposite to the weight (see Fig. 6.1). But the lift is now at right angles to the path of the glide, while the drag acts directly backwards parallel to the gliding path.

If the argument has been followed so far, there will be no difficulty in under­standing the problem of maximum endurance for jet-driven aircraft. Since fuel consumption is roughly proportional to thrust, we shall get maximum endurance by flying with minimum thrust, i. e. with minimum drag. So the endurance speed of a jet aircraft corresponds closely to the range speed of a propeller-driven aircraft, and from the comfort point of view, this makes the jet aircraft easier to fly in the condition of maximum endurance.

Since the thrust, and hence the consumption, should be the same at the same indicated speed at any height, it should not matter at what height we fly for endurance.

Summary

Table 5.5 and Fig. 5.13 summarise the difference between jet and propeller – driven aircraft so far as range and endurance are concerned. They must be considered as a first approximation only – they take into account the aero­plane efficiency for the propeller-driven type (neglecting propeller and engine efficiency), and both aeroplane and propulsive efficiency for the jet-driven type (neglecting engine efficiency). All this means is that the more important factors have been taken into account, and the less important factors have been neg­lected. It is not the whole story, and should not be considered as such.

The figures in brackets in Table 5.5 are the speeds in knots for the particular aircraft that has been considered in this chapter.

Fig 5.13 Power, drag and drag/speed curves

Before leaving this important subject it should be made clear that flying control regulations, made in the interests of safety, may sometimes make it necessary to fly at flight levels which do not exactly correspond to the best interests of either aircraft or engines.

Can you answer these?

1. What are the four most important forces which act upon an aeroplane during flight?

2. What are the conditions of equilibrium of these four forces?

3. Are these forces likely to alter in value, and to move their line of action during flight?

4. Explain how it is that an aeroplane can fly level at a wide range of air speeds.

5. Is the relationship between air speed and angle of attack the same at height as at sea-level?

6. What is the effect of weight on the relationship between air speed and angle of attack?

7. On a propeller-driven aircraft –

(a) Why will we get less range if we fly too high?

(b) At what height should we fly for best endurance?

(c) Why is the air speed for best endurance different from the air speed for best range?

8. On a jet-driven aircraft –

(a) Under what conditions should we fly for maximum range?

(b) At what height should we fly for maximum range?

(c) At what speed and height should we fly for maximum endurance?

For solutions see Appendix 5.

In Appendix 3 you will find some simple numerical examples on the problems of level flight.