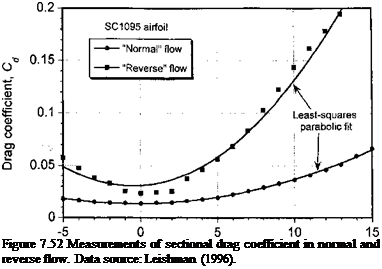
Unsteady Attached Flow
A prerequisite in any unsteady aerodynamic theory is the ability to model accurately the unsteady airloads at the blade element under attached flow conditions. In the first instance, the most elementary level of approximation is to consider incompressible, 2-D flow. This avoids the need to model the wake from other blades (a problem considered in detail in Chapter 10) and allows convenient analytical and semi-analytical mathematical solutions to be incorporated into the rotor analysis. However, the helicopter rotor analyst is still faced with several compromises. First, the assumptions and limitations of any model must be properly assessed and understood. For example, neglecting the compressibility of the flow is not readily justified for rotor problems. This justification requires that not only must the local free stream Mach number be low, but the frequency of the source of unsteady effects must be small compared to the sonic velocity, that is, the product ooc/a <$C 1, where a is the speed of sound. This means that the characteristic reduced frequency must also be small. The reduced frequency can be written as к = a>c/2Ma, so that Mk <$C 1 to justify the assumption of incompressible flow. Second, any model must be written in a mathematical form that can be coupled into the structural dynamic model of the rotor system. For example, in some cases it may be desirable to write the aerodynamic model at each blade element as sets of ordinary differential equations. Third, because the blade element unsteady aerodynamic model is contained within radial and azimuthal integration loops, computational time considerations are important, and this alone can limit the allowable level of sophistication possible with any mathematical model of unsteady aerodynamics.
The most fundamental approach to the modeling of unsteady aerodynamic effects is through an extension of steady, 2-D thin-airfoil theory. This gives a good level of analysis of the problem and provides considerable insight into the physics responsible for the underlying unsteady behavior. Results for unsteady airfoil problems have been formulated in both the time domain and the frequency domain, primarily by Wagner (1925), Theodorsen (1935),
Kiissner (1935), and von Karman & Sears (1938). These solutions all have the same roots in incompressible, unsteady thin-airfoil theory and give exact analytic (closed-form) solutions for the pressure distribution (hence, the forces and pitching moments) for different forcing conditions (i. e., for perturbations in AoA or an imposed nonuniform vertical distribution of chordwise velocity). While these methods are valid for 2-D and incompressible flows, and were primarily intended for fixed-wing aeroelastic applications, they have also formed the foundation for several extensions to subsonic compressible flow and also to specific types of rotating-wing problems. For example, one extension of Theodorsen’s theory was developed by Loewy (1957), which is a solution that approximates the effects of the shed wake vorticity below the rotor, as laid down by the blade and by other blades.
The unsteady compressible (subsonic) thin-airfoil problem has also received considerable attention – see, for example, Lomax et al. (1952) and Lomax (1968). Even though in some cases the local flow may have an incident Mach number that may be low, the product Mk must still be much less than unity if the incompressibility of the flow is to be justified. Because the governing equation in a compressible flow is the hyperbolic wave equation compared to the elliptic nature of Laplace’s equation for incompressible flow [see Karamcheti (1966)], unsteady aerodynamic theories cannot be obtained in a corresponding exact, convenient analytical form. There are, however, some limited exact solutions and numerical solutions available. These can be used to great advantage in the development of semi-analytic or semi-empirical methods for unsteady subsonic compressible flows, which are formulated in the spirit of the classical incompressible theories but are still computationally practical enough to be included within helicopter rotor analyses.











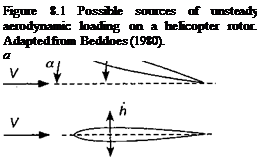
 Pitch (from blade controls & torsional response)
Pitch (from blade controls & torsional response)
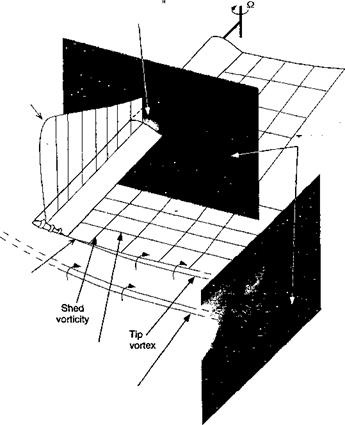

 0 F-i ■ – T–I ■’ ‘-і … ………………………………………… І ■ іЧфг-ч І… і, т-^
0 F-i ■ – T–I ■’ ‘-і … ………………………………………… І ■ іЧфг-ч І… і, т-^