Non-convex Effects

Up to now radiation cooling on completely convex surfaces was considered.

On real configurations surfaces may at least partly face at each other, which reduces the radiation-cooling effect: the surfaces receive radiation from each other and therefore the cooling effect is partly canceled. We call this a “non­convex effect”. Such effect happens at wing roots, fin roots, between fuselage and winglet etc. In the extreme, in an inlet, in a combustor, but also in a gap of a control surface no radiation cooling is possible at all [2]. However, radiative energy transport may nevertheless play a role in such cases [16].

We treat now the reduction of the radiation cooling effect due to non­convex effects following the approach of R. K. Hold and L. Fornasier [29, 30]. It is important to understand that the situation at radiation-cooled aerothermo – dynamic surfaces is different from that at surfaces of, for instance, satellites. Here the (characteristic) thicknesses of the boundary layers of the involved surfaces, which themselves depend to a large extent on their wall tempera­tures, introduce a strong non-linear coupling. This coupling does not exist at satellites. There the heat is simply exchanged without any couplings to flow properties. Nevertheless, the descriptive problems are the same (heat balances, sight lines between surface elements).

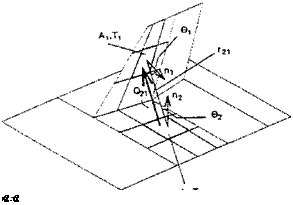Consider the situation in Fig. 3.7.

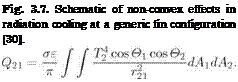The rate of energy Q2 radiated from A2 and acting on Ai is [29]

(3.28)

The surface element Ai absorbs the heat flux

<Zi, ab = -£%. (3.29)

Ai

Note that the absorption coefficient is equal to the emissivity coefficient— Kirchhoff’s law—when radiation is in equilibrium with the surface [17]. This is the case with the radiation-adiabatic surface. The actual flight situation, with a finite, but generally small, heat flux qw into the wall, can be considered as a quasi-equilibrium situation.

With the heat flux emitted from A1

qi, em = svTl, (3.30)

a balance can be made for A1:

Aqi = qi, em + qi, ab = є (vT? – ■ (3-31)

If we treat this equation in analogy to the Stefan-Boltzmann law, a “fic­titious” emissivity coefficient £f can be defined,[24] which in a computation method simply replaces the surface emissivity coefficient є in the radiation wall-boundary condition [29]:

This is the basic formulation of the problem. In [30] it is shown, that actually diffuse reflection must be regarded too in order to get results with high accuracy.

To apply the fictitious emissivity coefficient method with or without dif­fuse reflection, an influence matrix for the whole discretized configuration is to be computed, taking into account the sight lines between the individual surface elements. Because of the coupling of the radiation cooling effect to the boundary-layer thickness (see the discussion above), the fictitious emissivity coefficient must be determined iteratively.

This can easily be done during time-dependent integrations of the Navier – Stokes/RANS equations. With approximate methods or boundary-layer methods, special iteration approaches are necessary. The authors of [29] have devised a General Thermal Radiation (GETHRA) module, which can be in­corporated into any computation scheme. It regards the mentioned diffuse reflection and also “third part” reflections, which may be important in half­cavity situations, like, for instance, the front part of an inlet.

The fictitious emissivity approach is valid for external flow-field applica­tions and high surface-material emissivity coefficients, but can also be em­ployed in computation methods for rocket nozzle flows, TPS gap flows, etc. [3]. It has the advantage that it gives a vivid picture of non-convex effects and not only the plain result. For internal radiation problems, for instance

in combustors, less simplified methods, like the Poljak method etc., see, e. g., [31], should be applied.

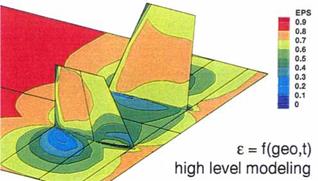
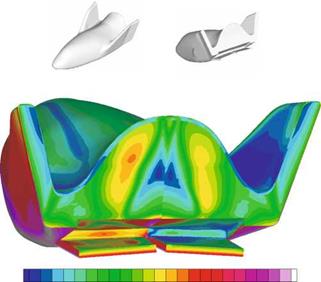
In the following figures we show the computed (Navier-Stokes/RANS equations) distribution of the fictitious emissivity coefficient at a generic sta­bilizer configuration, Fig. 3.7, [30], and the temperature distribution at the afterbody of the X-38 with and without non-convex effects regarded in the computation method [32].[25] The flight parameters are given in Table 3.2, the GETHRA module was employed for both cases.

Table 3.2. Flight parameters for the illustration of non-convex effects. Case Moo H [km] ReL L [m] a [°] є Boundary layer Ref. Generic config. 7 27 4.3-Ю7 7 -5 0.85 laminar [30] X-38 15 54.1 1.52-10® 8.41 40 0.80 turbulent [32]

The generic stabilizer configuration has a negative angle of attack in order to generate a bow shock, which does not interfere with the fins. The flow field was computed with a Navier-Stokes method with perfect-gas assumption. Fig. 3.8 shows that due to non-convex effects a reduction of the effective emissivity occurs in particular in the fin-root regions down to £f ~ 0.1. Consequently the radiation-adiabatic temperature (not shown) rises in such regions up to 1,500 K, compared to about 800 K ahead of the fins, where the non-convex effects diminish rapidly.

Fig. 3.8. Non-convex effects: distribution of the fictitious emissivity coefficient £f with high-level modeling at a generic stabilizer configuration [30].

At the X-38 we see a dramatic influence of non-convex effects in the half­cavity which is formed by the upper side of the body flap and the lower side of the fuselage, but also between the winglets and the fuselage, Fig. 3.9. In the half-cavity the fictitious emission coefficient goes down to £f « 0.05 (not shown). Similar low values are reached, although only on small patches, also at the winglets roots. The maximum temperatures in the half-cavity are around 1,200 K, if non-convex effects are regarded and only around 500 K, if they are not regarded. Between the winglets and the fuselage an average rise of approximately 100 K is observed, if non-convex effects are taken into account.

The forces and moments are not affected, which was to be expected be­cause the X-38 as a RV is compressibility-effects dominated, Table 1.1. The situation is quite different in this regard at a CAV, see Fig. 7.11 in Section 7.3.

Twall: 350 450 550 650 750 850 950 1050 1150 1250 1350 1450 Fig. 3.9. Non-convex effects: distribution of the radiation-adiabatic temperature Tra with high-level modeling at the afterbody of the X-38 [32]. Left side with, right side without non-convex effects taken into account.

These examples show that it is very important in hypersonic vehicle de­sign to monitor, and to quantify if necessary, non-convex effects, at least in order to arrive at accurate predictions of thermal loads. However, because thermal-surface effects influence, for instance, the viscous drag, Section 7.1, and other wall-near flow phenomena, they also must be considered in view of
vehicle aerodynamics, in particular regarding CAV’s but also ARV’s in their airbreathing flight mode.