Numerical and Experimantal Results

The aeroelastic behavior of the system "fbw-cascade" without taking into account the mechanical damping is defined by a the work coefficient value which is equal to the work performed by aerodynamic forces during one cycle of oscillations:

і

V

W = J M^dt, (5)

0

where c is the length of blade chord, ao is oscillation amplitude, M is aerody­namical moment, W is the aerodynamic work during one cycle of oscillation for torsional oscillations, and

і

V

W = J-F-vdt, (6)

0

for bending oscillations.

The work coefficients versus interblade phase angle (IBPA) for different fbw regimes and modes of oscillations are presented in Figures 5-7.

Figure 5 shows the work coefficient as function of IBPA for bending oscil­lations under incidence fbw angle which is equal to zero. The light squares (circles) correspond to the experimental data, the black squares (circles) cor­respond to numerical results. The negative values of work coefficient demon­strate the dissipation of an oscillating blade energy to the fbw (aerodamping), the positive values – to the transfer of the energy from the main fbw to the blade (flitter).

The strong infbence of both IBPA and Strouhal number on the aerodynamic stability of tune modes is seen in Figure 5. With decreasing of Strouhal number (increasing of the inlet fbw velocity) the stability decreases.

It should be noted that the work coefficient in dependence of IBPA has a typ­ical sinusoidal form. At the IBPA equal to 180 deg the maximal aerodamping is observed, at the IBPA near 0 deg the minimal aerodamping is found.

The quantitative and qualitative agreement between predicted and measured values is satisfactory.

In Figure 6 the variation of work coefficient versus IBPA for torsional oscil­lations under і = 0 and Sh = 0.616 is shown. The agreement between theoretical

Figure 5. The aerodynamic work coefficient in dependence of IBPA for the bending vibration (i = 0r, Strouhal Number – Sh = 0.2 – 0.616)

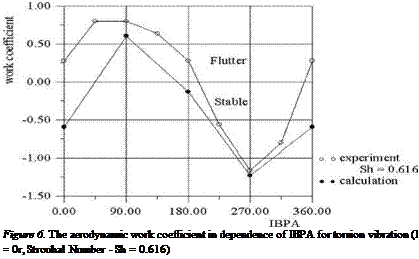and experimental results is good. For torsional oscillations in the range of 0 deg. < IBPA < 180 deg. the work coefficients have positive value that cor­responds to the transfer of energy from the flow to the oscillating blade. The maximal excitation occurs near 5 = +90 deg.

The aeroelastic characteristics at the bending vibration for the attack flow angle of 16 deg is presented in Figure 7. The agreement between the exper-

Figure 7. Aerodynamic work coefficient in dependence of IBPA for the bending vibration (i = 16r, Strouhal Number – Sh = 0.616)

imental and numerical results near the IBPA of 0 deg is seen although some discrepancy for IBPA of 180 deg is found.

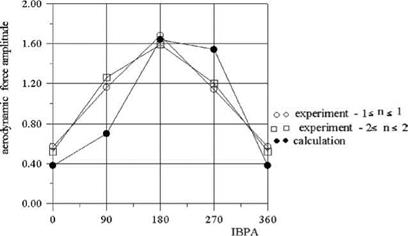
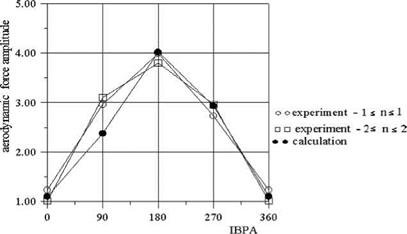
In Figures 8, 9 and 10 the calculated and measured amplitude of unsteady forces at the bending oscillations, for different incidence angles were shown. The calculation of the unsteady amplitude by using the aerodynamic inflience coefficients were done taking into account only four neighbouring blades (-1 < n < 1) and two neighbouring blades (-2 < n < 2). From results presented in these Figures it is seen that for considered flow regime taking into account only two neighbouring blades give the satisfactory agreement with numerical calculations.

3. Conclusions

1. A partially – integrated method based on the solution of the coupled aerodynamic-structure problem is used for calculation of unsteady 3D fbw through an oscillating blade row to determine the critical conditions of flutter initiation.

2. The numerical investigation has been performed to calculate aeroelastic response of the compressor cascade at the different flow regimes and laws of oscillations.

3. The comparison of calculated and experimental results for bending and torsional oscillations has shown a satisfactory quantitative and qualitative agree­ment.

Figure 8. Amplitude of unsteady aerodynamic force at the bending oscillations

Figure 9. Amplitude of unsteady aerodynamic force at the bending oscillations i = 0, Sh = 0.616

References

Bolcs A., Fransson T. H. (1986) Aeroelasticity in Turbomachines Comparison of Theoretical and Experimental Cascade Results, Communication du Laboratoire de Thermique Appliquee et Turbomachines, Nr.13. Lusanne, Epfel.

Bolcs A., and Fransson T. H. (1986). Aeroelasticity in Turbomachines Comparison of Theoret­ical and Experimental Cascade Results, Communication du Laboratoire de Thermique Ap­pliquee et Turbomachines, Nr.13, Appendix A5 All Experimental and Theoretical Results for the 9 Standard Configurations, Lusanne, Epfel.

Figure 10. Amplitude of unsteady aerodynamic force at the bending oscillations i = 16, Sh = 0.616

Stel’makh A. L., Kaminer A. A. (1981). Effect of the geometrical parameters of a compressor cascade on the limit of bending self-oscillations of blades caused by cascade flitter, Strength of Materials, 15, 1, 104-109.

Kaminer A. A., Stel’makh A. L. (1996). Effect of the aerodynamic connectedly between blades of the aerodynamic damping of their vibrations, and origin of cascade flitter, Strength of Materials, 14, 12, 1667-1672.

Kaminer A. A., Chervonenko A. G., and Tsymbalyuk V. A. (1988). Method for Studying Un­steady Aerodynamic Characteristics of Airfoil Cascades vibrating in a Three-Dimensional Flow. Preprint. Institute for Problems of Strength, Ac. Sci. of the Ukr. SSR, Kiev 1988 (in Russian).

Len A. D.,Kaminer A. A., Stel’makh A. L., Balalaev V. A. (1986). Loss of dynamic stability of torsional vibrations of blades due to cascade flitter, Strength of Materials, 18, 1, 76-80.

Gnesin V., and Rzadkowski R. (2000). The theoretical model of 3D flitter in subsonic, transonic and supersonic inviscid fbw, Transactions of the Institute of Fluid-Flow Machinery, No. 106, 45-68.

Gnesin V., Rzadkowski R. (2002). A Coupled Fluid-Structure Analysis for 3D Inviscid Flutter of IV Standard Configuration, Journal of Sound and Vibration, 251(2), 315-327.

Gnesin V., Rzadkowski R. and Kolodyazhnaya, L., V. (2000). A coupled fliid-structure analysis for 3D flitter in turbomachines, ASME paper 2000-GT-0380.

Rzadkowski R., Gnesin V. (2000). The numerical and experimental verification of the 3D invis­cid code, Transactions of the Institute of Fluid-Flow Machinery, No. 106, 2000, 69-95.

Rzadkowski R. (1998). Dynamics of steam turbine blading. Part two: Bladed discs, Ossolineum, WrocSaw-Warszawa.

Tsimbalyuk V. A. (1996). Method of measuring transient aerodynamic forces and moments on vibrating cascade, Strength of Materials, 28, 2, 150-157.

Tsimbalyuk V. A., Zinkovski A. P and Rzadkowski R. (2002). Experimental Investigation of Pal­isade Flutter for the Harmonic Oscillations, Proc. of the XV Conference of Flow Mechanics, Augustow, Poland