. The Aerodynamic Design of Aircraft

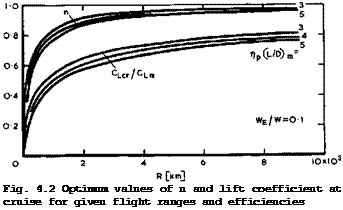which does not depend on the structural constants c^ and C2 . This cannot be solved explicitly, and we quote here some numerical values in Fig. 4.2, where WE/W has been kept constant, somewhat inconsistently; but less restric­ted calculations show the same trends, as it turns out that WE/W is nearly independent of R, in this first-order approximation. We find that the op­timum value value of n is near unity for longer ranges when fuel fraction is

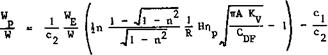large and the fuel weight matters more; and that n is noticeably smaller than unity for shorter ranges when the fuel fraction is small and the engine weight matters more. The values of the lift coefficient С^сг at cruise change correspondingly. With these values of n, a maximum of the payload is reached, which is given by

These first-order results lead to some important conclusions: whether an air­craft of the classical type is designed for flight over short or tong ranges, this task can be fulfilled by much the same layout – the aircraft look the same at first sight and have a strong family resemblance. For a given cruis­ing speed, the aerodynamic and propulsive parameters (L/D)m and np can be kept about the same. This means that the aspect ratio is high and nearly the same for all these aircraft and that the same kind of engine can be installed. The L/D-curves will then look much the same as the curves in Fig. 4.1, and only the operating point at cruise will move up or down curve (1) according to the range to be flown; at longer ranges (such as the transatlantic range), the operating point will be fairly close to (L/D)m ; at shorter ranges, it may be as much as halfway down.

As the fuel fraction increases with range, the wing loading at take-off will be the higher the longer the range, but the wing loading at landing can be much the same for all aircraft; if the demands on airfield performance are the

Properties of Classical and Swept Aircraft

same, on which the degree of complexity built into the high-lift system depends. This implies, in turn, that the payload fraction can be increased as the fuel weight is reduced and that it will be the greater the shorter the range, as can already be seen from the dominant factor 1/R in (4.12). All this con­firms that it is quite realistic to think in terms of a whole family or type of aircraft designed according to Cayley’s concept.

For a self-consistent set of the numerical values of the parameters involved, we illustrate by an example of a typical transatlantic aircraft of no excep­tional performance, Fig. 4.3, how the various weight items vary with n on either side of the optimum value. This should have a salutary and moderating effect on aerodynamicists in that it demonstrates very clearly how precarious it is for the aircraft designer to be left with a worthwhile payload; and also how much the mechanical and structural engineers, as well as the materials, avionics, and propulsion engineers can contribute to the success of an air­craft by providing lightweight solutions for their parts of the design. Fur­ther, the certification engineers can exert a very significant influence when they define safety standards and factors and conditions for environmental acceptability. For instance, an allowance has been made in the example of Fig,

4.3

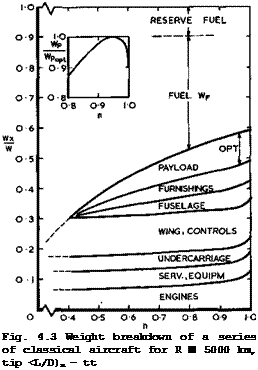for reserve fuel to cope with stand-off conditions, diversions etc; this

takes up about as much weight as the best payload, so that any changes in the rules for fuel reserves, brought about by improvements in air-traffic control, say, will have a proportional effect on the payload and hence on the economics of the aircraft.

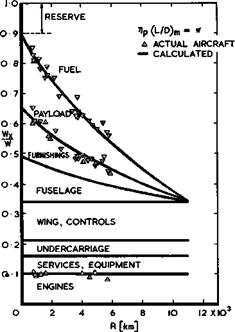
Fig. 4.4 shows a similar weight breakdown for a family of aircraft designed to fly over different ranges. This demonstrates how shorter ranges and hence less

The Aerodynamic Design of Aircraft

fuel weight allow the payload fraction to be increased and with it the weight of the fuselage and of the furnishings. Very roughly, half the weight of an aircraft on take-off is fuel if it is to cross the Atlantic Ocean. The points in Fig. 4.4 represent values for actual aircraft, the upward-pointing symbols

Fig. 4.4 Weight breakdown for a series of classical aircraft with optimum payloads for different flight ranges. Mq ■ 0.8

having been obtained by addition from the bottom and the downward-pointing symbols by subtraction from the top. Similarly, an inspection of the aspect ratios of actual transport aircraft, and of many of the more outstanding mili­tary aircraft, shows that the value of the aspect ratio is usually between 5 and 8, i. e. it is always high in an aerodynamic sense. Also, specialised air­craft, such as the LockspeiserLand Development Aircraft (see M Wilson (1975)), fit into the general framework. Gliders, which have no engine and carry no fu$l, and are designed to more stringent aerodynamic performance requirements, generally have higher aspect ratios and thus reinforce the conclusions drawn here. The aerodynamic design of gliders, nowadays often for two different design points for different purposes, is very instructive, and we refer to investigations by A Quast & F Thomas (1967), F Thomas (1971), and G Redeker (1975Dl

The theoretical framework presented here evidently provides a good representa­tion of the overriding trends in the characteristics of actual aircraft. This implies that classical aerofoil theory for wings of high aspect ratio, which has been discussed partly in Section 3.2 and will be discussed again in more detail in Section 4.3, goes well together with the engineering requirements of the classical type of aircraft. On reflection, and bearing in mind the very many conceptual abstractions, simplifications, and approximations which have to be made before we arrive at this theory, this is one of those striking and fortunate coincidences on which the aerodynamics of aircraft lives.

The assumptions made in this performance analysis are so drastic that it is of interest to know what the answer would be if more detailed and accurate para­meters of the airframe and engine were taken into account and also realistic assumptions made for the flight path and requirements during take-off and landing (see e. g. D Lean (1962), D H Perry (1969) and (1970), and J Williams

(1972) ) and for the range itself (see e. g. J F Holford et a£.(1972)). Such detailed calculations are made, anyway, in the actual design of aircraft where multivariate analysis is beginning to be used and to prove itself a useful tool. We refer here to such an analysis carried out by D L I Kirkpatrick

(1972) and (1973) on how the optimum design for payload is affected by changes in the mission requirements, the operational constraints, and the design stan­dards. This analysis shows that, in general, second-order effects arising from the complex interactions between the variations with range, aircraft size, fuel fraction, and wing loading and of the variations of passenger capacity and structural efficiency must be taken into account in an actual design but do not change the main trends established in the first-order analysis. For example, the aspect ratios of the wings of various turbojet aircraft of dif­ferent sizes, ranges, and ages (past and estimated future) should all be close to 7 and vary at the most between about 5 and 8 . Again, the value of the parameter n varies in much the same way with range as in Fig. 4.2, with some of the actual values slightly below those given there. The engine weight fraction may be below 0.1 (down to nearly 0.07) for some short-range aircraft and the wing loading at the approach may increase as the range decreases. We note also that the optimum design of a short-range aircraft, which does not need to carry fuel reserves, has a maximum lift-to-drag ratio which should be about 12% larger than that of an aircraft which does. There is also a bene­ficial effect of larger sizes (see e. g. D L I Kirkpatrick (1972), D KUchemann & J Weber (1968)).

Altogether, these results confirm that the first-order performance analysis gives a good guide to the required characteristics of classical aircraft de­signed according to Cayley’s principles, for the time being. But some of the aspects of the analysis are restricted to classical aircraft, and we shall see later that other types of aircraft require a different kind of performance an­alysis, even to a first order.

Before we discuss the design of the classical aircraft in more detail, we con­sider first an extension of this concept to include swept-winged aircraft, be­cause these are so closely related to one another that they can be treated together.