Shock Waves

In the following two sections we study normal and oblique shock waves and discuss the Rankine-Hugoniot conditions, which connect the flow properties upstream and downstream of them. We generally do not give tables and charts for the determination of the flow properties. For oblique shock waves, however, a chart is given with the shock-wave angle в as function of the flow-deflection angle S for a number of upstream Mach numbers Mi. Further given is a figure with the Prandtl-Meyer angle v as function of the upstream Mach number M1. Both the chart and the data for that figure—taken from [11]—are for perfect gas (air, у = 1.4).

6.3.1 The Normal Shock Wave

Consider the shock surface in Fig. 6.1 a). On the axis, the symmetric shock surface lies orthogonal to the supersonic free stream. Its thickness is very small compared to its two principle radii. We approximate the shock surface locally by a plane surface. If the body lies very far downstream, we can
consider the flow behind the normal portion of the shock wave as parallel and uniform, like the flow ahead of the shock wave.

With these assumptions we have defined the phenomenological model of the “normal shock wave”, that is a plane shock surface, which lies orthogonal to a parallel and uniform supersonic stream. Behind it the flow is again parallel and uniform, but subsonic: the normal shock wave is a strong shock wave.

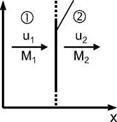
We study now the normal shock wave, like any aerodynamic object, in an object-fixed frame, Fig.6.8 (see also Fig. 5.4).[59] We know that the shock wave is a viscous layer of small thickness with strong molecular transport across it. In continuum flow it usually can be considered approximately as a discontinuity in the flow field. The flow parameters, which are constant ahead of the shock surface, change instantly across that discontinuity, Fig. 5.4 b), and are constant again downstream of it. How can we relate them to each other across the discontinuity?

normal shock Fig. 6.8. Schematic of a normal shock wave and notation.

Obviously there are entities, which are constant across the discontinuity, as is shown in the following. These are the mass flux, the momentum flux and the total enthalpy flux. We find the describing equations by reduction of the conservative formulations of the governing equations, eq. (4.83), eq. (4.33), and eq. (4.64) to one-dimensional inviscid flow (we omit dx)

d(pu) = 0, (6.39)

d(pu2 + p)=0, (6.40)

d(puh) — udp = 0. (6.41)

Eq. (6.41) can be combined with eqs. (6.3) and (6.39) to yield a form, which immediately can be integrated

dpu(h + – u2)] = 0. (6-42)

The integration then yields the constant entities postulated above:

Piui = P2U2, (6.43)

Piu2 + pi = P2u2 + P2, (6.44)

ріпі (hi + 5/2) = p2’U2 (ft? + (6.45)

The relation for the total enthalpy flux, eq. (6.45), reduces with eq. (6.43) to

hi + qiq = I12 + ^«2- (6.46)

This relation says, that the total enthalpy ht is constant across shock waves:

ht! = ht2 = ht. (6.47)

This important result is in contrast to that for the total pressure. We will see below, that pt is not constant across shock waves.

Relation (6.47) indicates also, that the maximum speed Vm is constant across the shock wave. For a perfect gas the total temperature Tt, the total speed of sound at, and the critical speed of sound a* are constant across the shock wave, too.

For the following considerations we assume perfect gas flow. We combine eqs. (6.43) and (6.46) and find

Pi, P‘2 , ,r.

——– b ‘Mi =——— h гг-2 • (6.48)

Piui P2U2

After introducing the critical speed of sound a*, we arrive at Prandtl’s relation[60]

and at the Rankine-Hugoniot relations

P2_ _ (7 + 1)P2 ~ (7 ~ l)pi Pi (7 + !)Pi – (7 – l)/>2 ’

P2 _ (7 + 1)P2 ~ (7 ~ l)Pi Pi (7 + l)Pi – (7 – 1)P2 ’

P2 – Pi P2 + P

———- = 7——- :—– •

P2 – Pi P2 + Pi

Eq. (6.49) can be written in terms of a Mach number related to the critical speed of sound M* = u/a* as

MФ1 M*2 = 1. (6.53)

The Mach number M* is related to the Mach number M by eq. (6.20). Both have similar properties, which are shown in Table 6.1.

Table 6.1. Relation of Mt and M. M 0 0.707 1 72 OO M* 0 / 7 + 1 V 7+3 1 7 + 1 7 + 1

Prandtl’s relation in either form implies the two solutions, that the flow speed ahead of the normal shock is either supersonic or subsonic, and behind the normal shock accordingly subsonic or supersonic, i. e., that we have either a compression shock or an expansion shock.

We developed the phenomenological model “normal shock wave” starting from a supersonic upstream situation. In our mathematical model we did not make an assumption about the upstream Mach number. The question is now, whether both or only one of the two solutions is viable.

Before we decide this, we give some relations for the change of the flow parameters across the normal shock wave in terms of the upstream Mach number Mi, and the ratio of specific heats 7, see, e. g., [11]:

6.65)

We make a plausibility check by putting M = 1 into the above relations. We find for the ratios of density, velocity, temperature, speed of sound, pres­sure, and total pressure, as well as for the Mach number M2 the values “1”, as was to be expected. The pressure quotient cp2 is zero, whereas the ratios of pressure to total pressure remain, also as to be expected, smaller than one.

The pressure coefficient at the stagnation point, cpt2, is the same as that for shock-free flow.

Now we come back to the question, which solution, that with supersonic or that with subsonic flow upstream of the shock wave, is viable. To decide this, we consider the change of entropy across the shock wave. We note from eq. (6.60) that a total pressure decrease is equivalent to an entropy rise.

We just plug in numbers into eq. (6.60), choosing 7 = 1.4. The results are given in Table 6.2. We find that only for Mach numbers Mi > 1 the total pressure drops across the shock, i. e., only for supersonic flow ahead of the normal shock we observe a total pressure decrease, i. e., an entropy rise. Hence the above relations for the change across the normal shock wave are only valid, if the upstream flow is supersonic.

Expansion shocks are not viable, because they would, Table 6.2 (the first four Mach numbers M1 < 1), lead to a rise of the total pressure, i. e., an entropy reduction, which is ruled out by the second law of thermodynam­ics. Of course, we should have known this from the beginning, because we introduced the shock surface as a thin viscous layer.

Table 6.2. Change of total pressure pt2/ptl = e (s2 sl)/R across a normal shock for selected upstream Mach numbers Mi and 7 = 1.4. Mi 0 /7 V 7 0.5 0.75 1 2 5 10 OO Pujpt! undefined. 00 2.256 1.037 1 0.721 0.062 0.003 0

The results given in Table 6.2 demand a closer inspection. We find from the second bracket of eq. (6.60) a singularity at

Ml = (6.66)

2Y

which with y =1.4 becomes M2 = 1/7.

Below that value the total pressure ratio across the normal shock is un­defined. From eq. (6.55) we see that for Mi = — l)/27 the temperature

behind the shock wave becomes zero, i. e., that for this upstream Mach num­ber the maximum velocity Vm, eq. (6.15), is reached.

The result thus is: if one assumes an expansion shock, the smallest pos­sible upstream Mach number is that, for which behind the shock the largest possible speed is reached. Behind this result lies the fact that in our mathe­matical model the conservation of the total enthalpy is assured also for the physically not viable expansion shock.

Just plugging in numbers as we did above is somewhat unsatisfactory. The classical way to show that only the supersonic compression shock is viable,
which however is restricted to Mach numbers not much different from Mi = 1, is to make a series expansion, which yields

— = eMS2~Sl)/fi = і———— ——(Mі —l)3 + terms of higher order. (6.67)

Pti 3(Y + 1)2

Because of the odd exponent of the bracket of the second term on the right-hand side of the equation we see that indeed a total-pressure decrease, and hence an entropy increase, across the normal shock happens only for Mi > 1.

With this result we obtain from eqs. (6.54) to (6.57) that across the normal shock wave pressure p, density p, temperature T are increasing instantly, whereas speed u and Mach number M decrease instantly. The most important result is, that we always get subsonic flow behind the normal shock wave:

M2 I normal shock < 1 (6.68)

For large upstream Mach numbers, i. e., M1 ^ ж, we find some other in­teresting results.[61] They permit us, for instance, to judge in hypersonic flow— at large temperatures—the influence of a changed 7 on the flow parameters downstream of a normal shock.

We obtain finite values for the ratios of velocities, and densities, as well as for the Mach number and the pressure coefficient behind the normal shock for M1 ^ ж

u2 Y – 1 ui Y +1	(6.69)
P‘2 7 + 1 Pi Y – 1	(6.70)
M92 ->■ 7 “1, 27 ’	(6.71)

and for the pressure coefficients

(6.72)

and

Static temperature, speed of sound, and pressure ratios, however, for M1 tend to infinite values

obtained