THE z DERIVATIVES (Сг., CA, Cw Cm)

There are two main classes of z derivatives; those that are associated with ground proximity, and those that are associated with vertical gradients in the properties of the atmosphere. Of the latter the density gradient is the most important, and others can probably be ignored most of the time.

We have described some of the effects of ground proximity in Sec. 7.5. To calculate the associated г derivatives one needs the data, either theoretical or experimental, on the variation of the various coefficients with height above ground. For configurations with large power effects, i. e. strong slipstreams or jets impinging on the ground, testing is generally required to get good results. The ground effects can be very large, and the z derivatives can exert a very important influence on the vehicle dynamics at landing and take-off.

As to the effects of atmospheric gradients, the gradient dpldz has already been explicity included in the equations of motion (5.13,16), so that if T, D, L, M all vary exactly as p when the speed is constant then CTz etc. will all be zero. This assumption is probably good enough for D, L, and M, but not always for T. If the vehicle uses air-breathing engines, then T cc pis reason­able, and CTz = 0; but if a constant-thrust rocket is used, then we have

dTjdz = 0, and from the analysis on p. 183,

(7.12,1)

The only other atmospheric gradients that might need to he included are those associated with Reynolds number Be and Mach number M. Sometimes, for very high altitudes the particulate nature of air becomes a factor. The Knudson number

where 1 is the mean free path and l is a characteristic length of the vehicle, may then be used as an aerodynamic parameter. It is not a new independent variable, being related to M and Re:

_M

*„ = 1.267,- where у is the ratio of specific heats. For air a rough approximation is Kn M/Fe. The circumstances when these gradients might be important are those involving very rapid changes of the flow field with the parameter in question—for example, near M = 1, the variations of M with height due to sound-speed gradient; and near the Re for boundary layer transition. A typical derivative would be calculated thus. Let Gx stand for any of GT – • • Cm; then

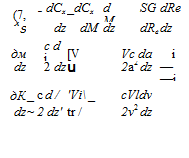
(7.12,2)

where

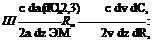and

7.13 AEROELASTIC DERIVATIVES

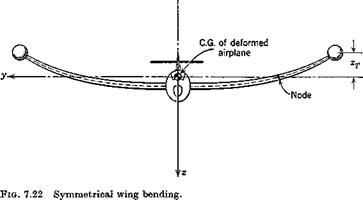
In Sec. 5.12 there were introduced certain aerodynamic derivatives associated with the deformations of the airplane. These are of two kinds: those that appear in the rigid-body equations, and those that appear in the added equations of the elastic degrees of freedom. These are illustrated in

this section by consideration of the hypothetical vibration mode shown in Fig. 7.22. In this mode it is assumed that the fuselage and tail are rigid, and have a motion of vertical translation only. The flexibility is all in the wing, and it bends without twisting. The functions describing the mode (6.12,1) are therefore:

у’ = У — Уо = 0 (7.13,1)

z’ = г — 20 = Цу)гт

For the generalized coordinate, we have used the wing-tip deflection zT. h(y) is then a normalized function describing the wing bending mode.

In view of the fact that the elastic degrees of freedom are only important in relation to stability and control when their frequencies are relatively low, approaching those of the rigid-body modes, then it is reasonable to use the same approximation for the aerodynamic forces as is used in calculating stability derivatives. That is, if quasisteady flow theory is adequate for the aerodynamic forces associated with the rigid-body motions, then we may use the same theory for the elastic motions.

In the example chosen, we assume that the only significant forces are those on the wing and tail, and that these are to be computed from quasisteady flow theory. In the fight of these assumptions, some of the representative derivatives of both types are discussed below. As a preliminary, the forces induced on the wing and tail by the elastic motion are treated first.