Navier-Stokes Equations

Writing the conservation laws of mass, momentum and energy including the vis­cous and heat conduction effects, in nondimensional form, reveals the following nondimensional parameters (see White [126]), 7, M0, Re, Pr, St, where

U p0Ul nCp fl

M0 = , Re = — , Pr = p, St = (12.180)

a.0 P0 k U

In the above formulas, k is the heat conductivity which is assumed to be propor­tional to p, and f is the characteristic frequency of unsteady motion. For reference quantities, a characteristic length of the body, l, free stream velocity U and density p0 are used.

There is one more nondimensional parameter defined as Da = tc/tm. The Damkohler number Da is the ratio of the characteristic time to establish chemi­cal equilibrium to the characteristic time of motion, tm = l/U. Da is very small for

chemical equilibrium and very large for frozen chemistry, while it is of order one for finite rate chemistry.

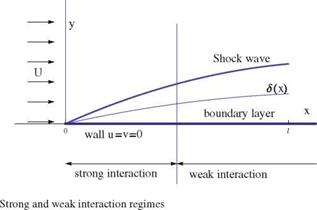
Under all the assumptions mentioned above, consider a flat plate in hypersonic flow (but with finite, not even very high Mach number) and assume laminar boundary layer with two regimes, strong and weak interactions as shown in Fig. 12.15.

Across the shock wave, kinetic energy is transformed into enthalpy and the result is high internal energy flow. Since the total enthalpy is constant across the shock, the downstream state is related to the upstream, undisturbed state by

1 2 1 2

H = h0 + – U2 = h + – У2 (12.181)

For hypersonic flows, У ^ U and h0 ^ h, then h ~ U2/2.

Using the space shuttle as an example (Cousteix et al. [27]), let U = 7.6 km/s, the temperature for a perfect gas would be T = 29,000 K! In reality, some of the energy is stored in the form of chemical energy in the process of dissociation and for real gas T = 6,000 K instead. Even for U = 2 km/s, corresponding to M0 = 6 (assuming Cp ~ 1 KJ/kg ■ deg), the adiabatic compression leads to a high value AT ~ 2,273 K, where

A considerable part of the heat is transported to the vehicle surface (if radiation is neglected).

In the flowing, the thermal boundary layer will be discussed for both isothermal and insulated (adiabatic) walls.

12.3.1 Laminar Boundary Layer in Weak Interaction Regime

For high Reynolds numbers, the viscous effects are confined to a layer next to the wall, of thickness S ^ l, and inside such a layer v ^ u. Based on order of magnitude analysis, the pressure does not vary across the boundary layer, hence the governing equations in two dimensions are (see Hayes and Probstein [127])

дpu дум дх + дy 0		(12.183)
дpu2 дрuv дp д дх + д y дх + д y	дu	(12.184)
^д y
др^,Н дpv Н д ( д T д ( дх + дy дy дy + дy ^	д^ /2	(12.185)
д y
where	1 2 u 2
p = pRT, and Н = CpT +	(12.186)
The energy equation can also be written in the form
( дT дT дp д ( дT (дu2 pCp Гдх +v —y) = ’‘Ш + ~y Vat) + )	(12.187)

see Liepmann and Roshko [128], Shapiro [129] and Schlichting [130]. The pressure gradient is determined by the external flow

dp d Ug dTe

— = ~peue~ = peCp —

dx dx dx

Since dp/дy ~ 0, the temperature and density are related and satisfy the relation

pT = peTe

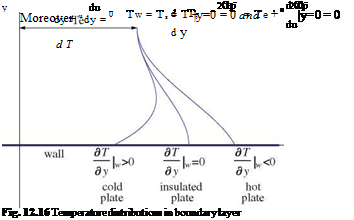
The wall boundary conditions are u = v = 0. Either Tw or дT/дy is specified at the wall. the thermal boundary layer is shown in Fig. 12.16.

Notice (дT/дy)y=0 > 0 for cold plate and (дT/дy)y=0 < 0 for hot plate.

The energy equation can be rewritten in terms of Pr (assuming Cp is constant)

дриН дpvH _ д ґ дH д // 1 дT

дх + ду ду ^ ду + дy Pr ду

For Pr = 1, the above equation admits a solution H = CpTs = CpT + u2/2 = const where the subscript s stands for stagnation.

Since u = 0 at the wall, it follows that the wall temperature is constant and equal to the stagnation temperature, i. e.

The temperature profile is given by

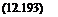
T = Te + lk (u2 – u2)

Notice that the stagnation temperature can be constant throughout the boundary layer only if the heat transfer is balanced by the work of viscous stresses or

therefore H is constant only when Pr = 1.

For the case of the flat plate, dp/dx = 0, a particular solution of the energy equation is H = u since the energy equation reduces to the momentum equation. More generally, let H = a + bu. To find a and b, we impose the boundary conditions u = 0 and T = Tw at y = 0 and T = Te and u = ue at the edge of the boundary layer. Thus the relation between u and T inside the boundary layer is given by

12 12 u

CpT + u = CpTw + Cp (Te — Tw) + ue

2 2 ue

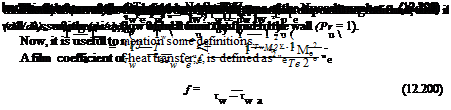Now, the heat transfer and skin friction at the wall are given by

or, in terms of wall properties

Cf w

Ch w = f Rew (12.203)

If Pr = 1, it is conventional to define the adiabatic wall temperature as

Ta = Te(1 + r l-1 M^ (12.204)

For laminar flow, r ~ fPr as demonstrated by Schlichting [130]. r is called the recovery factor and it represents the ratio of the frictional temperature increase of the plate to that due to adiabatic compression.