Strong Viscous/Inviscid Interaction

Lee and Cheng [138] obtained a uniformly valid solution for hypersonic strong interaction problem including the second order boundary layer correction due to the uneven heating and external vorticity created by the curved leading edge shock wave. In general, there exist between the inviscid region and the boundary layer an intermediate transitional layer as demonstrated by Bush [139]. Near the leading edge, the problem is more complicated because of the slip velocity and the temperature jump in the wall boundary condition.

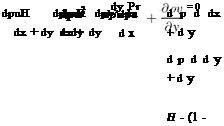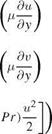Cheng and Novack [140] introduced a set of composite equations, with proper boundary conditions, to solve such problems numerically. The equations are the conservation of mass, tangential momentum and energy. In the latter two equations, the second order derivatives in the tangential direction are ignored. An approximate version of the normal momentum equation is used as follows

Cheng used a Crank-Nicolson scheme to obtain a numerical solution for attached flow over a flat plate, marching in the flow direction, on a relatively fine mesh (Ax/1 = 0.005 and Ay/5 = 0.01).

Cheng solve also blunt body problem with a similar set of equations in body fitted coordinates, where the transverse momentum equation is replaced by

d – = – Kc pu2 (12.222)

d y

where Kc is the longitudinal curvature of a reference surface.

Rudman and Rubin [141] and Rubin and Khosla [142] used similar formulations where they treated dp/дx term as a higher order term.

It is instructive to study the type of this set of equations. Following Vigneron et al. [143] and also Ref. [35], the streamwise pressure gradient дp/dx is multiplied by a coefficient ш.

For inviscid flows and w = 1, the equations are hyperbolic provided u2 = v2 > a2 and space marching is feasible. For 0 < w < 1, the equations are hyperbolic even in subsonic region provided

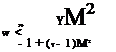(12.223)

where Mx = u/a.

For viscous flows, ignoring the first derivative in y, the conditions that the equa­tions are parabolic are

u > 0 and w < 2 (12.224)

– 1 + (y – 1) M2 У ’

hence, the so called parabolized Navier-Stokes (PNS) equations can be marched only for attached flows and with a fraction of the streamwise pressure gradient. However, w ^ 0 near the wall where Mx = 0. Lubard and Helliwell [144] showed that with backward difference approximation of dp/дx, there is a minimum Ax to be used for stability based of Fourier analysis and using finer meshes is not possible. See also Golovachov [39].

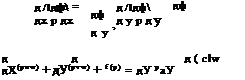The question about the type of the PNS equations can be clearly seen in terms of velocity/vorticity formulation. Let

The vorticity equation can be marched since it is a convection/diffusion/reaction equation, however, the streamfunction equation is of mixed elliptic/hyperbolic type. In the outer inviscid supersonic flow, it is hyperbolic while near the solid surface, the speed is low and the equation is of elliptic type allowing for upstream influence and reversal flow. In boundary layer approximation, the streamline curvature term is ignored and the stream function equation becomes

д 1 дф д у рд у w

and the system is of parabolic type. Therefore, it can be marched in space for attached flows. Couplings of Euler and parabolic equations are covered in Chap. 9.

To complete the formulation, the energy equation is solved for H or T and the pressure is calculated using the normal momentum equation in some form. The density is then calculated from the perfect gas law or its generalization.

It seems that marching the locally elliptic equation is a formidable task which appears in different forms in hypersonic flow research.

There are many attempts in the literature to use PNS with local separated regions using iterations locally. The obvious strategy is to use unsteady formulation to reach a steady state solution. Of course, such an option is more expensive.