Relevant properties of the turbulent boundary layer

A short review of the main parameters characterizing the turbulent boundary layer and used for the scaling of the wall pressure spectra is given in the following. Extensive discussions can be found in several textbooks [see e. g. Schlichting (1979)]; therefore we limit ourselves to reviewing some relevant parameters that influence the overall statistical properties of the wall pressure fluctuations field.

At the wall, the boundary layer exerts a shear stress tw, and there is a strong connection between this shearing and the behavior of the flow in the immediate vicinity of the wall. As the distance from the wall increases, the influence of the wall shear on the fluid motion diminishes and the flow properties may be described in terms of the local free stream velocity U and the thickness of the boundary layer S, this symbol denoting the so-called Blasius thickness. In this region, the flow behavior is usually called wake — like. Thus, depending upon the distance from the wall, two important flow regions can be identified. A layer close to the wall, where the velocity depends upon the fluid viscosity and the local wall shear, and an outer layer, where the velocity depends on the external properties of the flow (i. e. UTO, S and the upstream history of the layer). In the near wall region, the velocity increases linearly for increasing distance from the wall. In the outer layer the velocity defect evolves according to the well-known logarithmic law. Of course, due to the turbulent nature of the velocity field, the two regions boundaries can be defined only statistically.

In the linear region, the velocity gradient is independent of the distance from the wall. This assumption yields the following relationship:

Ui = — (23)

where the subscript 1 denote the velocity component on the streamwise (x) direction and m is the dynamic viscosity of the fluid.

In the logarithmic region the turbulence activity is the greatest and the velocity gradients are proportional to the distance from the wall. This gives rise to the logarithmic velocity profile described by the following equation:

where ln(-) is the natural logarithm of •. The quantity UT is called the friction velocity and it is defined as

being p the fluid density at ambient temperature. The coefficient k in Eq. 24 is the so-called Von KArman constant, equal to approximately 0.4 for any type of wall. B is a coefficient that depends only on the degree of surface roughness. The notation commonly used to represent the dimensionless quantities, is the following:

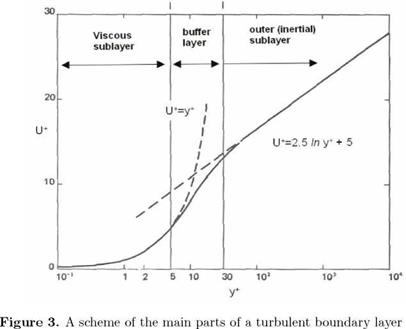In Figure 3 a simplified scheme of the turbulent boundary layer is re­ported for completeness.

Throughout the major portion of the fully developed turbulent boundary layer, the mean velocity profile over both smooth and rough walls satisfies

a defect law of the following form:

where Ue is the external velocity, outside the boundary layer. The function W(y/S) has been introduced by Coles (1956) and it is given by:

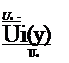It is well know that the definition of the Blasius thickness S is not suitable for turbulent boundary layers. It is better to introduce more objective definitions. Very briefly we remind the definition of displacement thickness S* based on a mass balance in the boundary layer and given by the following expression:

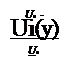Of course also S* is an outer scale because its magnitude is of the order of the depth of the viscous sublayer. Typically, S* is approximately equal to a fraction of S, from 1/8 to 1/5, depending on the surface roughness and the pressure gradient. Similarly, another length scale can be defined on the basis of the momentum balance. It is called the momentum thickness в and it is given by the following expression:

The ratio of the two length scales is called the shape factor:

S*

H=в <31>

According to the laws of the wall described above, it is possible to determine explicit relationships among set of boundary layer thickness and the friction factor. We refer to more specific textbooks for the details [e. g. Schlichting (1979)].

By integrating along y, between 0 and S, the momentum balance equa­tion written on x, it is possible to determine an equation relating integral quantities characterizing the turbulent boundary layer. This relationship, often denoted as the Von Karman integral equation, reads:

Cf _ de в Ґ 2 + H dP 2 dx 2 у I pU^J dx

being Cp the static pressure coefficient.

Empirical relationships are used also to determine the inner properties of the turbulent boundary layer once the outer scales are known either exper­imentally or numerically. In this case, by the knowledge of в, it is possible to empirically determine Cf and then UT. This approach is of common use since the estimation of UT by the direct measurement or computation of tw might be very difficult in practice.

We finally remind that the velocity profile at high Reynolds numbers can be described by a power law of the following form [Schlichting (1979)]:

Ul = (У1 "

UT V 6 )

where typically n ~ 7 for smooth walls and 4 for rough walls. By considering the thickness definitions, the following relations are obtained:

6*

6

For n = 7 it is obtained 6*/6 = 1/8. Also Eqs. 37, 38 and 39 can be used for a qualitative estimation of the boundary layer integral properties.