Improved Newton’s Theory

The Newton’s impact theory gave us the surface pressure coefficient, Eq. 7.6, for the straight wall. On the other hand, experimental results show that the impact theory is also applicable for the blunt bodies in high Mach numbers. We know that at a high subsonic flow there is a strong detached shock in front of the stagnation point. If we use that stagnation pressure as a coefficient in Eq. 7.6, we get agreeable results between the Newton’s impact theory and experiments for hypersonic flow.

If Cpo denotes the stagnation pressure coefficient of the blunt body, the improve form of Eq. 7.6 reads as

Cp ffi Cpo sin2 dw (7.7)

At the stagnation point hw = p/2. This makes Eq. 7.7 yield better results than Eq. 7.6 for the hypersonic flows.

Assuming the detached shock in front of the stagnation point as a normal shock and using the normal shock relations in terms of the Mach number and pressure,

Fig. 7.2 Flow about a blunt body at high Mach numbers

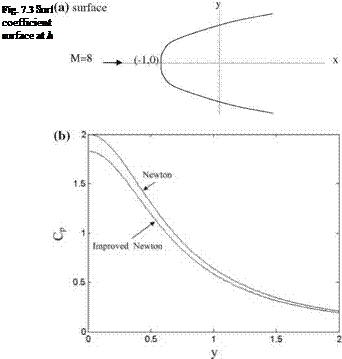
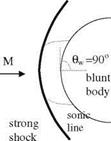it is possible to obtain the stagnation pressure to be used in Eq. 7.7 (see Problem 7.1). Improved Newton formula gives good results for the high angle of attack flows with high wall angles. Shown in Fig. 7.2a is the parabolic surface given by x = 0.729y2 — 1.0, and in Fig. 7.2b is the surface pressure coefficient plots obtained by Newton and improved Newton formula at M = 8.

The surface curvature effect is not taken into account in Eq. 7.7 when applied to a surface given in Fig. 7.3 while computing the surface pressure coefficient. For this reason it seems it is necessary to add the centripetal force effect in Eq. 7.7. In order to express the relation between the centripetal force and the normal component of the pressure gradient, it is convenient to use s-n coordinate system

Fig. 7.4 Balancing of the centripetal force with pres­sure gradient

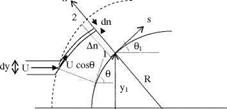where s is the tangential and n is the normal coordinates. The centripetal force acting in a unit volume is pV2/R where V shows the flow speed and 1/R shows the radius of curvature. The pressure force gradient which balances the centripetal force can be written as

Op pV2

On R

The continuity equation applied for a tube across the shock to equate the mass flux before and after the shock gives pVdn = p? Udy where U is the free stream speed and p? density, Fig. 7.4.

Integrating Eq. 7.8 from point 1 at the surface to the point 2 without crossing the shock along An gives

If we use the continuity equation in Eq. 7.9 we obtain

У1 +An cos 01

f p – UV d

P2 – P1 = – R dy

0

Taking the limit as An approaches to zero in Fig. 7.4, and expressing the radius R in terms of tangent angle 0 to the surface with V = U cos 0 gives

y1

P1 = P2 + p-U^d0) sin 01 cos 0dy (7.11)

Equation 7.11 in terms of pressure coefficient reads as

CP1 = CP2 + 2^“^ sin 01 cos 0dy (7.12)

Now, we can express Eq. 7.12 in terms of the pressure coefficient at point 2, shown in Fig. 7.4 at which the curvature effect is no longer exists, as follows

(7.13)

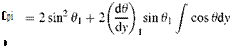For axially symmetric bodies the expression reads as

The theory developed by the centripetal force inclusion in evaluation of surface pressure is name the Newton-Busemann theory. Although inclusion of the cen­tripetal force seems correct because of physical considerations, it makes the pressure coefficient more disagreeable with the experimental results. The second term of the right hand side of Eq. 7.13 is just a theoretical term, i. e., it is not related to effect of the pressure waves increasing compressibility in the flow direction (Anderson 1989), which makes its implementation rare in engineering applications.