Normal Shock Waves. and Related Topics
Shock wave: A large-amplitude compression wave, such as that produced by an explosion, caused by supersonic motion of a body in a medium.
From the American Heritage Dictionary of the English Language, 1969
8.1 Introduction
The purpose of this chapter and Chapter 9 is to develop shock-wave theory, thus giving us the means to calculate the changes in the flow properties across a wave. These changes were discussed qualitatively in Section 7.6; make certain that you are familiar with these changes before continuing.
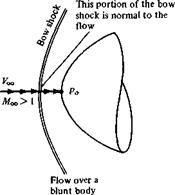
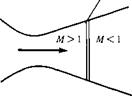
The focus of this chapter is on normal shock waves, as sketched in Figure lAb. At first thought, a shock wave that is normal to the upstream flow may seem to be a very special case—and therefore a case of little practical interest—but nothing could be further from the truth. Normal shocks occur frequently in nature. Two such examples are sketched in Figure 8.1; there are many more. The supersonic flow over a blunt body is shown at the left of Figure 8.1. Here, a strong bow shock wave exists in front of the body. (We study such bow shocks in Chapter 9.) Although this wave is curved, the region of the shock closest to the nose is essentially normal to the flow. Moreover, the streamline that passes through this normal portion of the bow shock later impinges on the nose of the body and controls the values
|
|
|
|
of stagnation (total) pressure and temperature at the nose. Since the nose region of high-speed blunt bodies is of practical interest in the calculation of drag and aerodynamic heating, the properties of the flow behind the normal portion of the shock wave take on some importance. In another example, shown at the right of Figure 8.1, supersonic flow is established inside a nozzle (which can be a supersonic wind tunnel, a rocket engine, etc.) where the back pressure is high enough to cause a normal shock wave to stand inside the nozzle. (We discuss such “overexpanded” nozzle flows in Chapter 10.) The conditions under which this shock wave will occur and the determination of flow properties at the nozzle exit downstream of the normal shock are both important questions to be answered. In summary, for these and many other applications, the study of normal shock waves is important.
Finally, we will find that many of the normal shock relations derived in this chapter carry over directly to the analysis of oblique shock waves, as discussed in Chapter 9. So once again, time spent on normal shock waves is time well spent.
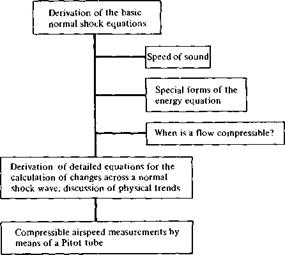
The road map for this chapter is given in Figure 8.2. As you can see, our objectives are fairly short and straightforward. We start with a derivation of the basic continuity, momentum, and energy equations for normal shock waves, and then we employ these basic relations to obtain detailed equations for the calculation of flow properties across the shock wave. In addition, we emphasize the physical trends indicated by the equations. On the way toward this objective, we take three side streets having to do with (1) the speed of sound, (2) special forms of the energy equation, and (3) a further discussion of the criteria used to judge when a flow must be treated as compressible. Finally, we apply the results of this chapter to the measurement of airspeed in a compressible flow using a Pitot tube. Keep the road map in Figure 8.2 in mind as you progress through the chapter.
|
Figure 8.2 Road map for Chapter 8. |