Viscous Hypersonic Flow and Aerodynamic Heating

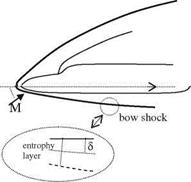
There are two important reasons to consider the real gas effects in hypersonic flows. The first reason is to predict the viscous drag on the body, and the second is to determine the heating caused by the high velocity gradients of the very high free stream speeds which is to stagnate on the body. The heating effect is much more at the stagnation points of the slender bodies as compared with that of blunt bodies. For example, the heating at the nose of a re-entering slender body is three times more than that of space shuttle (Anderson 1989). On the other hand, the drag caused by the strong detached shock is very high. However, the skin friction drag becomes higher for the slender bodies because of having thinner boundary layers as opposed to the boundary layers of blunt bodies. In addition, we have to keep in mind that because of low density yielding low Reynolds numbers, the boundary layers of hypersonic flow must be thick compared to the low speed flows which is somewhat contrary to the common practice. Moreover, behind the detached shock occurring at the nose of a blunt body there exist a layer in which the entropy change is strong. This layer is thicker than the boundary layer and the entropy gradient in this causes extra vorticity even outside of the boundary layer as shown in Fig. 7.14. The Crocco

theorem gives the relation between the entropy gradient and the vorticity generated by this gradient as follows (Liepmann and Roshko),

Vxm = —T grad S (7.48)

For this reason, while studying the hypersonic flow about a blunt body, the entropy change must be considered.

Now, it becomes necessary to derive the formula for the boundary layer thickness in terms of the Reynolds and the Mach numbers of the flow. As we recall from the incompressible viscous theory, the boundary layer thickness d is inversely proportional with the square root of the Reynolds number, i. e., at station x the boundary layer thickness: d / хД/R. In the compressible boundary layer both the density and the viscosity changes considerably with temperature. Therefore, let us write the Reynolds number in terms of the viscosity and the density at the station x on the surface d / x/ppwUex/pw. Here, the subscript e refers to the boundary layer edge and w denotes the wall conditions. Now, we can write the boundary layer thickness as follows:

According to the boundary layer assumption, the pressure remains constant at a given station. Therefore, with the perfect gas assumption we have pe/pw = Tw/Te, and by assuming linear dependence of viscosity on absolute temperature Eq. 7.49 becomes

If we assume the wall temperature as the adiabatic stagnation temperature at high Mach numbers, the relation between the temperature ratio and the edge Mach number becomes Tw/Te % (y — 1)/2M2, and the hypersonic boundary layer thickness reads as

d M2e

x Re

According to Eq. 7.51 the hypersonic boundary layer thickness is proportional with the square of the Mach number.

We have seen that the boundary layer thickness in hypersonic flows grows very thick. For a flat plate at zero angle of attack, on the other hand, the pressure remains the same along x. Is this still possible for very large Mach numbers? The answer to this question lies in the parameter defined as v = pC—=.

If we assume that the viscosity linearly changes with temperature in the boundary layer, we can write pe/pw = CTe/TW. Let us denote the displacement thickness of a boundary layer at zero angle of attack with d*. The slope of the

surface because of the displacement thickness then reads as he = dd*/dx. According to the Piston theory, for Ив ^ 1a linear approach gives us the pressure distribution from Eq. 7.26 as follows

Pw =Pi = 1 + уИв = 1 + yMdd*/dx (7.52)

Here, at high Mach numbers the slope в for the adiabatic wall conditions can be approximately written as dd*/dx ffi (у — 1)/2M2/C/vR and when substituted in Eq. 7.52 to give

PwlPi = 1 + у(у — 1)v/2 (7.53)

This interaction is called the weak interaction.

For strong interaction, i. e. for Mh ^ 1 (Hayes and Probstein 1966) we obtain

Pw/Pi ffi у(у + 1)M2(dd*/dx)2/2 (7.54)

The slope в for the flat plate is dd*/dx % [(у — 1)/2]1/2(M2C/Re)1/4 (Anderson 1989). Hence, for the strong interaction we have

Pw/Pi у(у2 — 1)/2V (7.55)

For both, weak and strong interaction the surface pressure formula for the specific heat ratios of у = 1.4

Pw/Pi ffi 1 + 0.464v (7.56)

The Reynolds number depends on x, and in Eq. 7.56 the Reynolds number is in the denominator of the second term which means around the leading edge that term becomes very large and the wall pressure becomes very large. As a result of viscous interaction, the pressure around the leading edge becomes very high compared to the pressure of the ideal flow. This is the indicative of very high drag and intense heating around the leading edge for the case of hypersonic flows. The depiction of this interaction in terms of the wall to free stream pressure ratio for the flow about a flat plate is shown in Fig. 7.15.

Shown in Fig. 7.15 is the hypersonic strong viscous interaction at the leading edge of the flat plate to create induced pressure zone. Since there is a considerable pressure change at the leading edge region the analysis of the boundary layer in hypersonic flow must be quite different from the classical approach. In addition, since the interaction at the leading edge region is strong, the effect of the leading edge on the stations away from the stagnation point is still felt strongly even in the weak interaction zone. Therefore, the boundary layer solutions obtained in the weak interaction region in hypersonic flow is quite different from the classical boundary layer solutions.

At the leading edge of a flat plate because of the term with 1/(x)1/2 in Eq. 7.56, the pressure theoretically goes to infinity for finite Mach numbers as sketched in Fig. 7.15. In practice however, reaching to those high Mach numbers only happens during re-entry at high altitudes where the density of the atmosphere is so low. The low density at those altitudes makes the mean free path of the air molecules quite high compared to the dimensions of the leading edge which in turn makes the assumption of continuum no longer valid. For this reason, in order to obtain more realistic results for the pressure about the leading edge, instead of continuum approach, molecular models are preferred with the slip conditions on the surface to replace no-slip conditions as boundary conditions. Using slip conditions helps reducing the pressure values with the Mach number and helps giving results in agreement with the experimental values (Anderson 1989). So far we have seen the viscous interaction for the flat plate in hypersonic flow.

Now, we can further extend the interaction analysis and give a brief summary for different type of bodies in hypersonic flow. If we know the pressure distri­bution pc over a conical surface then because of viscous interaction the induced pressure difference approximately reads as follows (Talbot et al. 1958)

P^ = 0.12*c 0 < Xc = m3 PcJR~< 4 (7.57)

Pc

Here, c denotes the potential flow conditions at the conical surface.

In hypersonic flow, the viscous interaction lowers the lift to drag ratio, L/D, by increasing Mach number. This effect is more for the blunt nosed bodies with blunt shapes as opposed to the slender bodies with wings. The maximum L/D ratio is 1.7 for a cone with half cone angle of 9° at M = 9, and it drops down to L/D = 0.5 at M = 19 (Anderson 1989). For a space capsule type of bodies, on the other hand, the L/D ranges between 0.4 and 0.2.

The serious problem of the viscous interaction in Hypersonic flow is the aerodynamic heating. First, let us study the heat transfer problem for a flat plate in high speed flow. If we let qw be the heat transfer for a unit area in a unit time, we have

qw StpeUe (had hw) (7.58)

Here, St is the dimensionless Stanton number, had and hw are the adiabatic wall temperature and the value of the enthalpy at the wall, respectively. The famous Reynolds analogy states that the Stanton number is related to the skin friction

coefficient Cf = sw/(1/2peU^) with St % cf2 (Schlichting). The enthalpy differ­ence had — hw in Eq. 7.58 is the main factor of the surface heating in high speed flows. The value of the enthalpy at the wall is the value obtained by solving the energy equation with adiabatic wall conditions. Using the engineering approach, the recovery factor r is employed to define the relations between the adiabatic wall enthalpy, boundary layer edge conditions e and the stagnation enthalpy h0 to give the following

had = he + rU2e/2 and h0 = he + U^/2 (7.59a, b)

From Eq. 7.59a, b we obtain

had he

h0 – he

Here, the free stream stagnation enthalpy is always greater than the adiabatic enthalpy of the wall to make r is always less than unity.

Defining the Prandtl number as the ratio between the viscous energy loss and the heat conduction, i. e., Pr = icp/k, for the flat plate in hypersonic flow condi­tions the Blasius solution gives (White 1991)

r ffi/PT (7.61)

Equation 7.61 is valid for a wide range of Mach numbers with 2% accuracy. This gives a relation between the Stanton to surface friction ratio in terms of the Prandtl number as follows

St/cf = 1/2P-2/3 (7.62)

Equation 7.62 is also valid with 2% accuracy for a wide range of Mach numbers. Although Eq. 7.62 is obtained for flows around the flat plate, it has been applied to determine the aerodynamic heating caused by three dimensional slender bodies (Anderson 1989).

In case of turbulent hypersonic flow past flat plate with increase in Mach number, there is a considerable decrease in Stanton number. According to the Van Driest’s turbulent flow data while Mach number is ranging from 0 to 10, the Stanton number decreases to 0.1 of its incompressible value.

So far we have seen the aerodynamic heating for the slender bodies with sharp leading edges. The solution for stagnation point of the flat plate was singular. Now, we can analyze the aerodynamic heating for the bodies with blunt noses. The analysis of heat transfer at the stagnation point of the circular cylinder and sphere was made by Van Driest (1952), and the following formula for the heat transfer was provided (Anderson 1989):

Cylinder : qw = 0.57P-0 6(peie)1//dUe/dx(haW – hw) (7.63a, b)

Sphere : qw = 0.763Pr -0b(pei()1/1 dUe/dx(haw – hw)

Here, Ue is the boundary layer edge velocity and it naturally takes the value of zero at the stagnation point. The derivative of the edge velocity with respect to x at the stagnation point is non zero, and it is inversely proportional with the local radius of curvature. Assuming Newtonian flow, the derivative of the edge velocity reads as

dUe_ 1 2(pe – pi)

dx R pe

Here R, is the radius of curvature at the stagnation point (see Problem 7.32). If we substitute Eq. 7.64 in Eq. 7.63a, b, the heat transfer at the stagnation point of the circular cylinder for hypersonic flow reads as

The aerodynamic heating is inversely proportional with the radius of curvature of the stagnation point. This fact forces the hypersonic vehicles to have a round nose as shown in Fig. 7.9 of the re-entering space capsule. The change in the Stanton number at the stagnation point of a cylinder is experimentally observed to be proportional with the inverse square root of the radius of curvature as given in Eq. 7.65. Naturally, as we move away from the stagnation point, the aerodynamic heating reduces considerably. At W = 45° on the surface, halfway between the stagnation point and the shoulder, this reduction goes down to half the value of the stagnation heat transfer, and at the shoulder where W = 90°, the heating becomes the one tenth of the stagnation value (Anderson 1989).

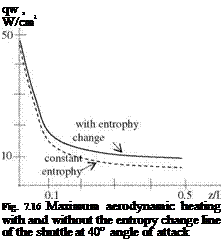
We have stressed the role of viscous effect concerning aerodynamic heating. In the no slip condition which causes high velocity gradients, i. e. high vorticity value is due to viscosity. In addition, the high entropy gradient occurring behind the strong bow shock generates a vorticity field as given by Eq. 7.48 and creates an entropy layer as shown in Fig. 7.14. The vorticity generated by the entropy gra­dient also creates non negligible aerodynamic heating starting from the stagnation point. Shown in Fig. 7.16 are the maximum aerodynamic heating values on the line, which is the symmetry line of the bottom surface of the space shuttle, with and without entropy change considered.

According to Fig. 7.16, the difference between the results obtained with entropy and without entropy is small near the stagnation region, and it increases monotonically in the flow direction as the entropy layer increases (Anderson 1989). The results obtained by considering the entropy gradient are agreeable with the experimental measurements, and therefore, they should be preferred.

The last subject to be studied in hypersonic heating is related to the interaction of the strong shock and the boundary layer. This type of heating is usually gen­erated by the oblique shock which is created at a slender leading edge of an external body of hypersonic air vehicle. Since this shock is inclined, it strikes another external part which is located at downstream, and reflects from the boundary layer to generate heat. For the first time, this type of heating is

encountered because of the oblique shock created at the intake of an engine interacting with the boundary layer on the engine-body junction of a hypersonic plane in a test flight (Neumann 1972). The sketch and the effect of the k shock are shown in Fig. 7.17a, b. The variation of the Stanton number and the surface pressure are given in Fig. 7.17b around the region where the shock boundary layer interaction is taking place.

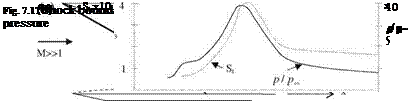
As seen in Fig. 7.17b, the variation of Stanton number is closely related to the surface pressure variation. Right after the k shock, the value of Stanton number at the surface increases eight times (Marvin et al. 1975). This increase in the Stanton number is the indicative of the aerodynamic heating due to shock boundary layer interaction. The surface pressure increase, on the other hand, is tenfold across the shock. Now, we can obtain the relation between the pressure change and

the aerodynamic heating using the variation of the Stanton number. In laminar flow, the skin friction coefficient Cf is inversely proportional with the Reynolds number. Since the Stanton number is proportional with the skin friction coefficient, the following relation can be deduced

St / 1/vRffi» wqe (7.66)

Since the pressure is proportional with the density, the definition of the surface heating, qw becomes

qw / pp (7.67)

to give the proportionality of aerodynamic heating with pressure.

In turbulent flows there is a relation between the surface friction and the Reynolds number as follows: Cf ^ 1/(Re)1/5 (Schlichting). The relation between the surface heating and surface pressure for turbulent flow then becomes

qw / (pe)4/5 (7.68)