Modelling helicopter flight dynamics: trim and stability analysis

The challenge and responsibility of modern engineering practice demand a high level of creative activity which, in turn, requires the support of strong analytical capability. The primary focus should be on the engineering significance of physical quantities with the mathematical structure acting in a supporting role.

(Meriam 1966)

4.1 Introduction and Scope

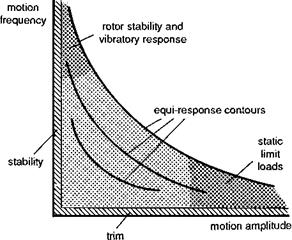
Meriam’s words of advice at the head of this chapter should act as a guiding light for engineers wishing to strengthen their skills in flight dynamics (Ref. 4.1). In Chapter 3 we sought to describe the physics and mathematics required for building a simulation model of helicopter flight behaviour. This chapter takes the products of this work and develops various forms of analysis to gain insight into how helicopters behave the way they do, hence establishing the engineering significance of the physics. Within the framework illustrated in our reference Fig. 4.1, the mechanics of helicopter flight can be described in terms of three aspects – trim, stability and response – as shown by the regions highlighted in the figure. The trim problem concerns the control positions required to hold the helicopter in equilibrium. The aircraft may be climbing, turning and may be at large angles of incidence and sideslip, but if the three translational velocity components are constant with the controls fixed, then the aircraft is in trim. Strictly, climbing and diving flight cannot be described as trim conditions, because the changing air density will require continual corrections to the controls. Provided the rates of climb or descent are relatively small, however, the helicopter will be, practically speaking, in trim. Stability is concerned with the behaviour of the aircraft following a disturbance from trim. Classically, static stability is determined by the initial tendency (i. e., will the aircraft tend to return to, or depart from, the initial trim?), while dynamic stability concerns longer term effects. These are useful physical concepts and will be embraced within the more general theory of the stability of the natural modes of motion, developed from the linear theory of flight mechanics. Response to pilot control inputs and to atmospheric disturbances are essentially nonlinear problems, but some insight can be gained from extending the linear approximations to finite amplitude motion. We shall return to response in Chapter 5. Trim, stability and response make up the flying characteristics. Later in Chapters 6 and 7, the reader will find that these flying characteristics are part of the domain of flying qualities. These later chapters will be concerned with how to quantify and measure flying quality, while here in Chapters 4 and 5 we are more interested in the physical mechanisms that generate the response.

Fig. 4.1 The territory of helicopter flight mechanics

Typical problems tackled by the flight dynamicist through mathematical mod­elling include

(1) determination of the control margins at the operational flight envelope (OFE) and safe flight envelope (SFE);

(2) design of flight control laws that confer Level 1 handling qualities throughout the OFE;

(3) simulation of the effects of tail rotor drive failure in forward flight – establish the pitch, roll and yaw excursions after 3 s;

(4) derivation of the sensitivity of roll attitude bandwidth to rotor flapping stiffness;

(5) establishing the tailplane size required to ensure natural pitch stability at high speed;

(6) determination of the effects of main rotor blade twist on power required for various missions;

(7) establishing the maximum take-off weight, hence payload, of a twin-engine heli­copter while conforming to the civil certification requirements for fly-away capa­bility following a single engine failure;

(8) assessment and comparison of various candidate aircraft’s ability to meet the flying qualities standard – ADS-33.

Of course, we could continue adding more tasks, but the range of problems has, hope­fully, been adequately demonstrated with the above list. Setting down this ‘short list’ of activities, some of which the author has been intimately involved with over the past 20 years, serves as a reminder of the importance of modelling in aircraft design and development – relying on experiment to tackle these problems would be prohibitively expensive. This is, of course, not to devalue or diminish the importance of flight testing.

Before we engage the supporting mathematics for describing the trim and stability problems, it may be useful for the reader to explore how all three are encapsulated in the relatively simple problem of heave motion in vertical flight. The key equations taken from Chapter 3 relate to the thrust coefficient Ct and uniform component of inflow Л0 through the rotor (eqns 3.91, 3.139):

This approximation of uniform rotor inflow is strictly applicable only when the blade twist has the ideal variation, inversely proportional to radius, giving constant circulation across the rotor and minimum induced drag. Linear blade washout of 10° or more generally gives a reasonably good approximation to the ideal loading.

In its simplest form, the trim problem amounts to determining the collective pitch 00 required to hold a hover, which is often written in terms of the equivalent pitch at the three-quarter radius, rather than at the rotor hub; i. e., from eqns 4.1 and 4.2, we can write

For moderate values of thrust coefficient (Ct — 0.007) and typical values of solidity (s = Nbc/пR ~ 0.09), the collective required to hover is approximately doubled by the presence of the induced velocity. The rotor torque required is then the sum of the induced and profile contributions (eqn 3.116)

C15

ce = cQi + cQp = ^Д + cQp (4.4)

showing the nonlinear relationship between torque and thrust in hover.

The trim problem is generally formulated as a set of nonlinear algebraic equations. In the case examined, the unique solution was obtained by simple rearrangement. In a more general trim, when the relevant equations are coupled, this will not be as straightforward and recourse to numerical solutions will be necessary.

Analysis of the dynamic stability and response problems requires the formulation of the equation of motion relating the normal acceleration to the applied thrust

Z _ T Ma =—M

Stability and response characteristics may be assessed (in the first approximation) by analysis of the linearized form of the nonlinear eqn 4.5. We write the normal velocity (w = Й Rhz in hover) as the sum of a trim or equilibrium value (subscript e) and a perturbation value

w = We + &w

If we assume that the Z force acting on the helicopter in the hover is an analytic function of the control во and normal velocity w, together with their time rates of change, then the force can be expanded as a Taylor series about the trim value (Ref. 4.2), in the form

9 Z 9 Z 1 92 Z 2 9 Z

Z = Ze +– Sw +– 8во +— ~ w2 + ••• + Sw + ■

9w 9в0 0 2 9w2 9w

In the simple form of thrust equation given by eqn 4.5, there are no unsteady aerody­namic effects and hence there are no explicit acceleration derivatives. For small and slow changes in w (i. e., Sw) and во (i. e., Seo), the first two (linear) perturbation terms in eqn 4.7 will approximate the changes in the applied force, i. e.,

9Z 9Z

Ze + — Sw +—————– Seo

e 9 w 9в0 0

The stability problem concerns the nature of the solution of the homogeneous equation

w — Zww = 0

where we have subsumed the aircraft mass Ma within the heave damping derivative Zw without any dressing, which is normal practice in helicopter flight dynamics, i. e.,

In eqn 4.9, we have used lowercase w for the perturbation in heave velocity away from the trim condition (cf. eqn 4.8 Sw ^ w, assumed small). This will be the general practice throughout this book, lowercase u, v and w, p, q and r denoting either total or perturbation velocities, depending upon the context. It is clear that the solution of eqn 4.9 will be stable if and only if Zw is strictly negative, as then the solution will be a simple exponential subsidence.

The heave damping derivative can be estimated from the derivative of thrust coefficient with rotor heave velocity

9 Ct 1 / 9^0 2a0sk0

9^z 2 у 9^z J I6A0 + a0s

giving the result

Z 2a0 AbP(Q R)k0

(І6Л0 + a0s)Ma

which ensures stability. The damping derivative, or the heave eigenvalue (see Appendix 4B), typically has a value of between —0.25 and —0.4 (1/s) and, from eqn 4.12, is a linear function of lift curve slope, a0, and is inversely proportional to blade loading (Ma /Ab). The natural time constant of helicopter vertical motion in hover is therefore relatively large, falling between 4 and 2.5 s.

The response to small collective control inputs is governed by the inhomogeneous linear differential equation

where the thrust derivative

d Ct 8 / aosko

BOq 3 16ko + aos )

is used to determine the control derivative

The ratio of the control derivative to the heave damping gives the steady-state response in heave velocity to a step change in collective pitch as

The rate sensitivity, or the steady-state rate per degree of collective, is seen to be a function of tip speed only. The rate of climb following a step input in collective is therefore independent of disc loading, lift curve slope, air density and solidity according to the simplifying assumptions of momentum theory. These assumptions, of which uniform inflow and constant lift curve slope are probably the most significant, were discussed at the beginning of Chapter 3.

The nature of the response to a vertical gust was described in some detail in Chapter 2, the equation of motion taking the form

W — Zww = Zwwg (t) (4.17)

The initial vertical acceleration is given by the product of the heave damping and the gust strength. A vertical gust of 5 m/s gives rise to a bump of about o.2 g for the higher levels of vertical damping. Reducing the blade loading has a powerful effect on the sensitivity to vertical gusts according to eqn 4.12, although overall, the helicopter is relatively insensitive to vertical gusts in the hover.

Helicopter vertical motion in hover is probably the simplest to analyse, but even here our simplifying approximations break down at higher frequencies and amplitudes, as unsteady aerodynamics, blade stall and rotor dynamic effects alter the details of the motion considerably. We shall return to this example later in Chapter 5. More general helicopter motions, in both hover and forward flight, tend to be coupled, and adequate single degree of freedom (DoF) descriptions are a rarity. As we progress through Chapters 4 and 5 however, the approach outlined above will form the pattern – that is, taking the basic nonlinear equations from Chapter 3 for trim and then linearizing for stability, control and small perturbation response analysis.

Chapter 4 is structured as follows. The techniques for describing and analysing trim and stability are set down in Sections 4.2 and 4.3 respectively. The expressions for the general trim problem will be derived, i. e., a turning, climbing/descending, sideslipping manoeuvre. Stability analysis requires linearization about a trim point and an examination of the eigenvalues and eigenvectors of the system. The key, 6 DoF, stability and control derivatives will be highlighted and their physical significance described. The natural modes of motion predicted from 6 DoF theory are also described. One of the major aids to physical interpretation of helicopter dynamic behaviour comes from the various approximations to the full equations of motion. Section 4.3 deals with

this topic, principally with linear, narrow range approximations that highlight how the various aerodynamic effects interact to shape the natural modes of helicopter motion. Working with modelling approximations is at the heart of a flight dynamics engineer’s practice, and we aim to give this area ample attention in both Chapters 4 and 5 to help the serious reader develop the required skills. The underlying mathematical methods used draw heavily on the theory of finite dimensional vector spaces, and Appendix 4A presents a summary of the key results required to gain maximum value from this chapter.

The theory of the stability of helicopter motion will be continued in Chapter 5, with special emphasis on constrained motion. The response problem is inherently nonlinear and typical behaviour will also be described in Chapter 5, with solutions from forward and inverse simulation. Discussion on some of the important differences between results using quasi-steady and higher order rotor models is also deferred until Chapter 5.

In order that some of the fundamental physical concepts of helicopter flight me­chanics can be discussed in terms of analytical expressions, it is necessary to make gross approximations regarding the rotor dynamic and aerodynamic behaviour. We include all the assumptions associated with Level 1 modelling as discussed at the be­ginning of Chapter 3, and then go further to assume a simple trapezoidal downwash field and ignore the in-plane lift loads in the calculation of rotor forces and moments. These latter effects can be important, but assuming that the lift forces are normal to the disc plane leads to a significant simplification in the trim and stability analyses. In most cases, this assumption leads to results that are 80% or more of the answer derived from considerably more complex rotor modelling and the resulting approximate theory can be used to gain the first-order insight into flight dynamics, which is particularly useful for the prediction of trends and in preliminary design.

We have already referred to Appendix 4A, containing the background theory of vector-matrix mechanics; two additional appendices complete the Chapter 4 series. Appendix Section 4B.1 presents the configuration datasets, including aerodynamic, structural, mass and geometric properties, for the three aircraft used in this book – the Lynx, Puma and Bo105. Appendix Section 4B.2 presents, in graphical form, the complete set of stability and control derivatives for the three aircraft predicted from two­sided numerical perturbations applied to the full Helisim nonlinear equations of motion. In the second edition of the book, a new Appendix Section 4B.3, presenting these derivatives and associated eigenvalues, is included. An analysis of the trim orientation problem is given in Appendix 4C.