Weak Oblique Shocks

We have seen that the compression of supersonic flow without entropy increase is possible only through the Mach lines. In the present discussion on weak shocks also, it will be shown that these weak shocks, which result when the flow deflection angle в is small and Mach number downstream of shock M2 > 1, can also compress the flow with entropy increase almost close to zero. It is important to note that, when we discussed about flow through oblique shocks, we considered the shock as weak when the downstream Mach number M2 is supersonic (even though less than the upstream Mach number M1). When the flow traversed by an oblique shock becomes subsonic (that is, M2 < 1), the shock is termed strong. But when the flow turning в caused by a weak oblique shock is very small, then the weak shock assumes a special significance. This kind of weak shock with both decrease of flow Mach number (M1 — M2) and flow turning angle в, which is small, can be regarded as isentropic compression waves.

For small values of в, the oblique shock relations reduce to very simple forms. For this case:

sin в & в and cos (в — в) & cos fi.

Therefore, Equation (9.168) simplifies to:

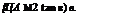Mj2 sin2 в — 1

Also, M2 > 1 for weak oblique shocks. Therefore, we may approximate this weak shock with both (Mj — M2) and в extremely small as a Mach line. Thus, the shock angle в can be regarded as almost equal to the Mach angle g. With this approximation, we can express tan в as follows:

1

sin в яь sin g = —

H M

cos в = л/1 — sin2 в

= —V7 M2 — 1 M v

1

tan в = -.

Vm2 — 1

Substituting for tan в in preceding equation, we get:

Mfsin2 в – 1 * I————– =^= в. (9.173)

2 VMM

Equation (9.173) is considered to be the basic relation for obtaining all other appropriate expressions for weak oblique shocks since all oblique shock relations depend on M1 sin в, which is the component of upstream Mach number normal to the shock.

It is seen from Equations (9.157) and (9.173) that the pressure change across a shock Ae, termed the shock strength can be easily expressed as:

P2 – P1 _ Ap ^ YM? в P1 Pi Vм? – 1 "

Equation (9.174) shows that the strength of the shock wave is proportional to the flow deflection angle в.

Similarly, it can be shown that the changes in density and temperature are also proportional to в. But the change in entropy, on the other hand is proportional to the third power of shock strength as shown below. By Equation (9.159), we have:

where m = (M? – 1) [Note that for weak oblique shocks under consideration, that is, for weak oblique shocks with (M1 – M2) ^ 1 and в very small, M2 sin2 в is approximated as M2.] For values of M1 close to unity, m is small and the terms within the parentheses are like 1 + e, with e ^ 1. Expanding the terms as logarithmic series, we get:

Now, let the wave angle в for the weak shock be different from the Mach angle i by a small angle e. That is:

в — 1 + e,

where e ^ /i. Therefore, sin в — sin (i + e) — sin i + e cos /i. Also, sin i — 1/M1 and cot i — vM – 1. Thus:

Mi sin в ^ 1 + e Vm2 – 1

or

m2 sin2 в ^ 1 + 2e vM2 – 1. From Equations (9.173) and (9.179), we obtain:

e — r±1JML

4 Mj2 – 1

That is, for a finite flow deflection angle в, the direction of weak oblique shock wave differs from the Mach wave direction i by an amount e, which is of the same order as в.