Supersonic Compression

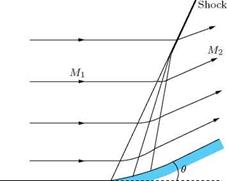Compressions in a supersonic flow are not usually isentropic. Generally, they take place through a shock wave and hence are nonisentropic. But there are certain cases, for which the compression process can be regarded isentropic. A compression process which can be treated as isentropic is illustrated in Figure 9.31, where the turning of the flow is achieved through large number of weak oblique shocks. These kinds of compression through a large number of weak compression waves is termed continuous compression. These kinds of corners are called continuous compression corners. Thus, the geometry of the corner should have continuous smooth turning to generate large number of weak (isentropic) compression waves.

The weak oblique shocks divide the field near the wall into segments of uniform flow. Away from the wall the weak shocks might coalesce and form a strong shock as illustrated in Figure 9.31. We have seen that the entropy increase across a weak wave is of the order of third power of deflection angle в. Let the flow turning through an angle, shown in Figure 9.31, be taking place through n weak compression waves, each wave turning the flow by an angle Ав. The overall entropy change for this compression process is:

(in – it) ~ п(Ав)3 ~ пАв(Ав)2 ~ в(Ав)2.

Thus, if the compression is achieved through a large number of weak compression waves, the entropy increase can be reduced to a very large extent, as compared to a single shock causing the same net deflection. When Ав is made vanishingly small, a smooth continuous turning of the flow as shown in Figure 9.31 is achieved. The entropy increase associated with such a continuous smooth compression process is vanishingly small, that is, the compression can be treated as isentropic.

At this stage it is natural to ask, whether this kind of isentropic compression is only of theoretical interest or it is used in practical devices too? The answer to this question is that it is used in practical devices too. For example, in the gas turbine engines used to propel supersonic aircraft such as fighters, the freestream supersonic air stream entering the engine intake needs to be decelerated to incompressible Mach numbers (of the order of 0.2) before reaching the combustion chamber, because with the present technology continuous and stable combustion is possible only at low incompressible Mach numbers. This can be achieved by a single normal shock or even with a strong oblique shock to decelerate the supersonic stream to a subsonic Mach number and then the subsonic stream can be decelerated further in a diffuser to reach the required incompressible Mach number before entering the combustion chamber. But both these decelerations will result in a large increase of entropy and the associated large pressure loss. This kind of large increase of entropy is desirable for an efficient mixing of fuel and air in the combustion chamber, but the severe pressure loss with the nonisentropic compression through the shocks is undesirable. We know that the engine is used to generate thrust by reaction. The momentum thrust produced by an engine is:

Thrust = m Vj.

where m is the mass flow rate of the combustion products of the fuel-air mixture burnt in the combustion chamber, expanded through the nozzle of the engine, and Vj is the flow velocity at the nozzle exit. By Bernoulli principle it is known that a large velocity Vj can be generated by expanding a gas at high stagnation pressure p0. Thus, the aim of the process through the engine is to achieve high p0. If possible we can use a compressor to achieve the desired level of p0. But carrying a compressor in a gas turbine engine is not a practically possible solution, mainly due to the weight penalty and the need for additional source of energy to run the compressor. Therefore, as an alternative, the high pressure required is achieved through combustion where liberation of thermal energy by burning a fuel-air mixture results in a large increase of total temperature Г0 and the associated increase of total pressure p0. Now, we will notice an interesting point if we keenly observe the process involved. The vehicle is flying at a supersonic Mach number. Because of the skin friction, shock and expansion waves around the vehicle and other drag producing causes the vehicle encounters drag. This drag has to be compensated with thrust to maintain the supersonic flight speed. Thus, the basic work of the engine is to supply the required momentum to compensate the momentum loss due to the drag. In other words, basically the loss caused by the drag can be viewed as loss of total pressure p0. Therefore, the engine must compensate the pressure loss in order to maintain the constant p0 required for the supersonic flight at the given altitude. Instead of adding the stagnation pressure equivalent to compensate for the pressure loss due to drag, we are doing the same thing in an indirect manner. This is done through combustion. For performing combustion, the supersonic air entering the engine is decelerated to low incompressible Mach number, fuel is mixed with the air and combustion is performed at such a low Mach number to increase p0 through the increase

of stagnation temperature Го. The combustion products at low-Mach number is accelerated through the engine nozzle to achieve the required jet velocity at the nozzle exit. In the deceleration process through shock/shocks at the engine intake, considerable total pressure is lost. Therefore, it would be appropriate and beneficial if the fuel is added to the air entering the engine with supersonic speed and the combustion is performed at the same freestream supersonic Mach number. But even though this is the most suitable and efficient situation, we are not in a position to do so. This is because the technology for performing stable combustion at supersonic Mach number is not yet established. Many research groups in various countries are working on establishing combustion at supersonic Mach numbers. Indeed, stable combustion at Mach number around 2 is reported by few advanced countries, such as USA, China, Britain, France and Japan. Once the technology for supersonic combustion is established, the pressure lost in decelerating the supersonic air stream to the incompressible Mach number to enable combustion with the present technology can be eliminated to a large extent. This will result in a significant increase of the engine efficiency. In other words, the pressure loss associated with the deceleration of supersonic or hypersonic flow entering the engine to the required incompressible Mach number for stable combustion with the present technology can be completely eliminated if technology is developed to perform stable combustion at supersonic/hypersonic Mach numbers.