Numerical Characteristics of Free-Wake Models

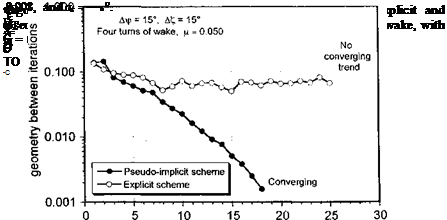The advantage of using an implicit or pseudo-implicit FVM is that many of the numerical and round-off error problems associated with explicit methods can be avoided. Typical convergence characteristics of an explicit and a pseudo-implicit FVM are shown in Fig. 10.36 for a relatively low advance ratio of 0.05, where the self – and mutually induced

effects from the tip vortices are strong. In each case, four complete turns of the free-vortex wake were used with a relatively coarse 15° azimuth step (A^0> = Ai/rw = 15°).[41] The

explicit scheme initially shows a converging trend, but only readies a minimum Єног ot about 0.05 after eight iterations. Further iterations cause numerical oscillations in the wake geometry and thereafter slowly drive the solution unstable. In contrast, the pseudo-implicit method essentially shows a monotonically converging solution, which converges below an acceptable error threshold after about fifteen iterations.

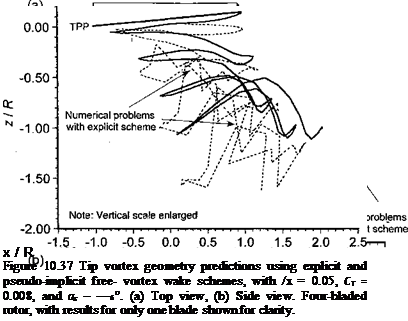
A comparison of the corresponding wake geometries at the end of the iteration cycles is shown in Fig. 10.37. Notice that with the explicit scheme there are several regions of the wake where the numerical errors have propagated, and there are significant signs of developing
instabilities that, based on experimental studies of helicopter rotor wakes [e. g., Lehman (1968) and others], are clearly not of physical origin. These are undesirable characteristics of free-vortex wake schemes using explicit integration schemes that make them unsuitable for rotor flow field predictions.