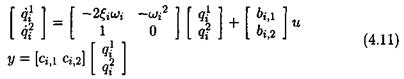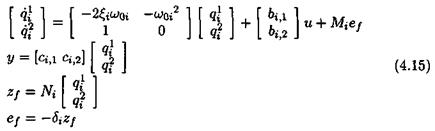Methods are described in this chapter for computing bounds of the real, complex or mixed s. s.v. /хд(М). Remember that M denotes in the following a complex matrix, which may correspond to the value of the transfer matrix M(s) at s = juj.
1. COMPUTATION OF THE REAL S. S.V.
The specific case of a model perturbation Д = diag(S), which only contains real non repeated scalars Si, is considered in this section.
1.1 A SOLUTION BASED ON THE MAPPING THEOREM
The definition of the unit hypercube D is first recalled:
D = {<5 = [Si… Jn] I Si Є R and |^| < 1} (5.1)
The s. s.v. g,, or its inverse the multiloop stability margin (m. s.m.) km, is defined as:
km — — = min(k I Є D s. t. det(I — kdiag(S)M) = 0) (5.2)
M
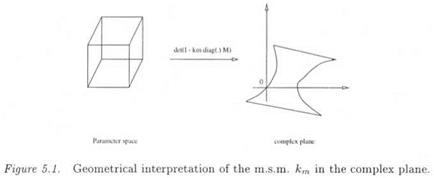
The m. s.m. km can thus be interpreted as the lowest value of k, such that the image of the unit hypercube D by the operator det(I – kdiag(S)M) contains the origin of the complex plane (see Figure 5.1 – this image is called a value set).
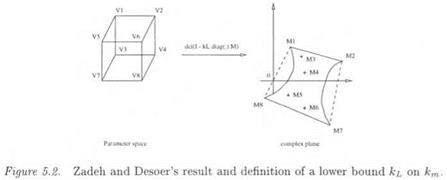
However, building this image is generally a computationally infeasible task. Nevertheless, in the special case of a model perturbation Д containing only non repeated real scalars Si, the operator dei(I – kdiag{S)M) is a complex multilinear function of vector S. It is thus possible to use a result in chapter 9 of (Zadeh and Desoer, 1963), which claims that the image of the unit hypercube D by the operator det(I – kdiag(S)M) is contained in the convex hull of the images Mi of the vertices Vi of D (Mapping Theorem). A lower bound ki of the m. s.m. km can thus be obtained as the smallest value of k, for which the convex hull contains the origin (see Figure 5.2).
Remarks:
(/’) The approach is exponential time, since an hypercube has 2” vertices when n parametric uncertainties Si are considered.
(ii) Like Zadeh and Desoer’s result, Kharitonov’s and edge theorems (Barmish and Kang, 1993; Bartlett et al., 1988) can also be interpreted in a frequency domain approach as Zero Exclusion Tests (Barmish and Kang, 1993). The difference between these three theorems is the way the uncertain parameters enter the plant model.
(iii) In the special case of a real matrix M (this especially occurs at the zero frequency, i. e. when M is the DC gain of the transfer matrix M(s)), the result by Zadeh and Desoer provides the exact value of the m. s.m. km. The convex hull coincides indeed with the image of the unit hypercube D by the operator det(I – km diag(S)M), since both sets he in the real axis.
The result by Zadeh and Desoer was used in (DeGaston and Safonov, 1988) as the basis of a computational algorithm, which provides the exact value of real ц using a branch and bound scheme. The idea is to partition the unit hypercube into a set of smaller hyperrectangles, and to apply Zadeh and Desoer’s result on each of these hyperrectangles, in order to decrease the conservatism of the lower bound кь of km. An upper bound of km (i. e. a p lower bound) is also computed to stop the partitioning process, when the gap between the bounds is sufficiently small: see (De – Gaston and Safonov, 1988; Ferreres et al., 1996a) for further details.
Remark: the algorithm in (DeGaston and Safonov, 1988) can be summarized in 3 operations, computing the lower bound, computing the upper bound and partitioning. Other algorithms with the same branch and bound structure were developed in (Chang et al., 1991; Balakrishnan et al., 1991; Newlin and Young, 1992). However, the aim of the algorithm in (Newlin and Young, 1992) is not to compute the exact value of mixed p, but rather to reduce the gap between the bounds to an acceptable value (typically 20 %), thus limiting as much as possible the exponential growth of computation with the number of uncertainty blocks (remember the problem of computing the exact value of p is NP hard).











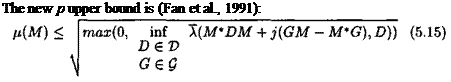
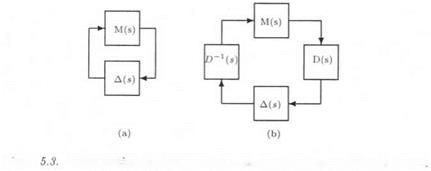 This theorem does not account for the structure of the model perturbation A(s). To this aim, a scaling transfer matrix l)(s) is used to decrease
This theorem does not account for the structure of the model perturbation A(s). To this aim, a scaling transfer matrix l)(s) is used to decrease