COMPUTATION OF SKEWED i BOUNDS
Two mixed v upper bounds and a mixed v lower bound are proposed in this chapter.
1. A FIRST і/ UPPER BOUND
Let Д a mixed structured perturbation (see equation (1.26)). Remember from chapter 5 that the sets V and Q of scaling matrices D and G are associated to Д:
|
|
Scaling matrix D must thus satisfy DA = AD.
Let Д = diag(AьДг), where Ді and Д2 are mixed structured perturbations. Let mi the dimension of Дг. Scaling matrices Dt associated to perturbations Д* are introduced, with ДДг = Д Д■ D 1 and £>2 are then defined as:
|
|
so that D = .Di + D2 is a scaling matrix associated to perturbation Д. Proposition 1..1 presents a first mixed v upper bound (see subsection 2.1 of chapter 5 for the definition of the quantities A (A, B) and r)(A, B)).
PROPOSITION 1..1 (Ferreres and Fromion, 1997)
u(M) < л /max(0, inf + Di)M – Dl + j(GM – M*G),D2)) (8.3)
у Di,£>2iC
Remarks:
(i) The optimal values of scaling matrices Z>i, D2,G in Proposition 1..1 can be computed with recent methods for solving LMIs: see chapter 5 (subsection 2.1).
(/’/’) The v upper bound of (Fan and Tits, 1992) is recovered when the model perturbation A only contains full complex blocks.
(in) The classical p upper bound of (Fan et al., 1991) can be obtained in Proposition 1..1 by taking Ai empty, so that Di = 0.
It is possible under mild conditions to compute the exact value of v by computing recursively the exact value of p (see subsection 4.2 of chapter 1). Analogously, Proposition 1..2 claims that it is possible to compute the и upper bound of Proposition 1..1 by computing recursively the /і upper bound of (Fan et al., 1991).
PROPOSITION 1..2 (Ferreres and Fromion, 1997) Let:
|
|
IfvuB(M) < oo, then vub(M) is the unique limit of the fixed point iterationafc+i = h(otk), where h is defined as:
|
|











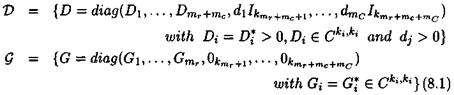


 : HflHX
: HflHX
 (resp. 0.5). The nominal degree of stability (resp. the nominal damping ratio) is 0.7 (resp. 0.61). The results of Figure 6.8 are of the same type as those obtained in the previous subsection.
(resp. 0.5). The nominal degree of stability (resp. the nominal damping ratio) is 0.7 (resp. 0.61). The results of Figure 6.8 are of the same type as those obtained in the previous subsection. uncertainties in the stability derivatives are 10%/0.229 « 43.5%. The robust stability properties of the flight control system are thus very good.
uncertainties in the stability derivatives are 10%/0.229 « 43.5%. The robust stability properties of the flight control system are thus very good.