Category Aerodynamics for Engineering Students

Flow of constant velocity parallel to Ox axis from left to right

Consider flow streaming past the coordinate axes Ox, Oy at velocity U parallel to Ox (Fig. 3.9). By definition the stream function np at a point P(x, y) in the flow is given by the amount of fluid crossing any line between О and P. For convenience the contour

Fig. 3.9

OTP is taken where T is on the Ox axis x along from O, i. e. point T is given by (x, 0). Then

ip = flow across line OTP = flow across line ОТ plus flow across line TP = 0 + U x length TP

= 0 + Uy

Therefore

ip=Uy (3.12)

The streamlines (lines of constant ip) are given by drawing the curves

ip = constant = Uy

Now the velocity is constant, therefore

ip

у = — = constant on streamlines

The lines ip = constant are all straight lines parallel to Ox.

By definition the velocity potential at a point P(x, y) in the flow is given by the line integral of the tangential velocity component along any curve from О to P. For convenience take OTP where T has ordinates (x, 0). Then

ф = flow along contour OTP = flow along ОТ + flow along TP = Ux + 0

Therefore

ф — Ux

The lines of constant ф, the equipotentials, are given by Ux = constant, and since the velocity is constant the equipotentials must be lines of constant x, or lines parallel to О у that are everywhere normal to the streamlines.

This flow is that associated with a straight line vortex. A line vortex can best be described as a string of rotating particles. A chain of fluid particles are spinning on their common axis and carrying around with them a swirl of fluid particles which flow around in circles. A cross-section of such a string of particles and its associated flow shows a spinning point outside of which is streamline flow in concentric circles (Fig. 3.7).

Vortices are common in nature, the difference between a real vortex as opposed to a theoretical line (potential) vortex is that the former has a core of fluid which is rotating as a solid, although the associated swirl outside is similar to the flow outside the point vortex. The streamlines associated with a line vortex are circular and therefore the particle velocity at any point must be tangential only.

Cross-section showing a few of the associated streamlines

Consider a vortex located at the origin of a polar system of coordinates. But the flow is irrotational, so the vorticity everywhere is zero. Recalling that the streamlines are concentric circles, centred on the origin, so that q$ = 0, it therefore follows from Eqn (2.79), that

£ = + ^ = o, i. e. — (r?,) = 0

r dr rdr

So d(rq,)/dr = 0 and integration gives

rq, = C

where C is a constant. Now, recall Eqn (2.83) which is one of the two equivalent definitions of circulation, namely

-f

In the present example, q-T= q, and ds = rdd, so

Г = 2 Trrqi = 2irC.

Thus С = Г/(2тг) and

dy> Г dr 27гг

and

2ттг

Integrating along the most convenient boundary from radius r0 to P(r, ff) which in this case is any radial line (Fig. 3.8):

Г г

= — -—dr (го = radius of streamline,^ = 0)

Jro 2lTr

Circulation is a measure of how fast the flow circulates the origin. (It is introduced and defined in Section 2.7.7.) Here the circulation is denoted by Г and, by convention, is positive when anti-clockwise.

Since the flow due to a line vortex gives streamlines that are concentric circles, the equipotentials, shown to be always normal to the streamlines, must be radial lines emanating from the vortex, and since

qD = 0, ф is a function of 6, and

Id ф Г r &6 2mr

Therefore

Аф = ^-<1в

Y Inr

and on integrating

Г

ф = — 6 + constant

2-к

By defining Ф — 0 when 6 = 0:

Ф = ±е (ЗЛІ)

Compare this with the stream function for a source, i. e.

Ф = ^ (Eqn(3.5))

Also compare the stream function for a vortex with the function for a source. Then consider two orthogonal sets of curves: one set is the set of radial lines emanating from a point and the other set is the set of circles centred on the same point. Then, if the point represents a source, the radial lines are the streamlines and the circles are the equipotentials. But if the point is regarded as representing a vortex, the roles of the two sets of curves are interchanged. This is an example of a general rule: consider the streamlines and equipotentials of a two-dimensional, continuous, irrotational flow. Then the streamlines and equipotentials correspond respectively to the equi­potentials and streamlines of another flow, also two-dimensional, continuous and irrotational.

Since, for one of these flows, the streamlines and equipotentials are orthogonal, and since its equipotentials are the streamlines of the other flow, it follows that the streamlines of one flow are orthogonal to the streamlines of the other flow. The same is therefore true of the velocity vectors at any (and every) point in the two flows. If this principle is applied to the source-sink pair of Section 3.3.6, the result is the flow due to a pair of parallel line vortices of opposite senses. For such a vortex pair, therefore the streamlines are the circles sketched in Fig. 3.17, while the equipotentials are the circles sketched in Fig. 3.16.

Place the source for convenience at the origin of a system of axes, to which the point P has ordinates (x, _y) and (r, 9) (Fig. 3.6). Putting the line along the. v-axis as ф = 0

Fig. 3.6

(a datum) and taking the most convenient contour for integration as OQP where QP is an arc of a circle of radius r,

ф = flow across OQ + flow across QP = velocity across OQ x OQ + velocity across QP x QP

„ m „
: 0 + -— x гв
2-кг

Therefore

or putting в = tan 1 (y/x)

, m і У ф = — tan“- 2t x

There is a limitation to the size of в here, в can have values only between 0 and 2n. For ф = тв/2тг where в is greater Ijhan 2tt would mean that ф, i. e. the amount of fluid flowing, was greater than m m2 s, which is impossible since m is the capacity of the source and integrating a circuit round and round a source will not increase its strength. Therefore 0 < 9 < 27Г.

For a sink

ф = —(т/2-к)в

To find the velocity potential ф of a source

The velocity everywhere in the field is radial, i. e. the velocity at any point P(r, в) is given by q = л/q + q and q = qn here, since qt = 0. Integrating round OQP where Q is point (r, 0)

ф= qcosf3ds+ qcos/3ds

Joq JQP

= / qndr+ [ qtr89 = [ qndr + 0 Joq Jqp Joq

But

m

2irr

Therefore

fm m r

ф= I -—dr = —In— Jro 2-їїг 2n r0

where ro is the radius of the equipotential ф = 0.

Alternatively, since the velocity q is always radial (q = qn) it must be some function of r only and the tangential component is zero. Now

m дф

Therefore

(3.7)

In Cartesian coordinates with ф = 0 on the curve го = 1

ф = £1п^+ЇЇ

The equipotential pattern is given by ф = constant. From Eqn (3.7)

, m, ^ m,

ф = — In r — C where C = — lnro

There are three basic two-dimensional flow fields, from combinations of which all other steady flow conditions may be modelled. These are the uniform parallel flow, source (sink) and point vortex.

The three flows, the source (sink), vortex and uniform stream, form standard flow states, from combinations of which a number of other useful flows may be derived.

3.3.1 Two-dimensional flow from a source (or towards a sink)

A source (sink) of strength m( — m) is a point at which fluid is appearing (or disappearing) at a uniform rate of m( — m) m2 s. Consider the analogy of a small hole in a large flat plate through which fluid is welling (the source). If there is no obstruction and the plate is perfectly fiat and level, the fluid puddle will get larger and larger all the while remaining circular in shape. The path that any particle of fluid will trace out as it emerges from the hole and travels outwards is a purely radial one, since it cannot go sideways, because its fellow particles are also moving outwards.

Also its velocity must get less as it goes outwards. Fluid issues from the hole at a rate of mm2s . The velocity of flow over a circular boundary of lm radius is m/27rm s_l. Over a circular boundary of 2 m radius it is m/(2ir x 2), i. e. half as much, and over a circle of diameter 2 r the velocity is mj2nrms~l. Therefore the velocity of flow is inversely proportional to the distance of the particle from the source.

All the above applies to a sink except that fluid is being drained away through the hole and is moving towards the sink radially, increasing in speed as the sink is approached. Hence the particles all move radially, and the streamlines must be radial lines with their origin at the source (or sink).

(a) In Cartesian coordinates Let a point P(x, y) be on an equipotential ф and a neighbouring point Q(x + 6x, y + 6y) be on the equipotential ф + 6ф (Fig. 3.4). Then by definition the increase in velocity potential from P to Q is the line integral of the tangential velocity component along any path between P and Q. Taking PRQ as the most convenient path where the local velocity components are и and v:

Fig. 3.4 Thus, equating terms and

(3.2)

(b) In polar coordinates Let a point P(r, ff) be on an equipotential ф and a neigh­bouring point Q(r + Sr, в + 66) be on an equipotential ф + 6ф (Fig. 3.5). By definition the increase дф is the line integral of the tangential component of velocity along any path. For convenience choose PRQ where point R is (r + 6r, в). Then integrating along PR and RQ where the velocities are qn and qt respectively, and are both in the direction of integration:

бф = qnSr + qt(r + 6r)66

= qn6r + qtr66 to the first order of small quantities.

But, since ф is a function of two independent variables;

сі дф, дф

6ф=Tr6r * дё60

(3.3)

and

1 дф

Again, in general, the velocity q in any direction s is found by differentiating the velocity potential ф partially with respect to the direction s of q:

3.2 Laplace’s equation As a focus of the new ideas met so far that are to be used in this chapter, the main fundamentals are summarized, using Cartesian coordinates for convenience, as follows: (1) The equation of continuity in two dimensions (incompressible flow) du dv

я ‘ + я – — 0 dx ay

(2) The equation of vorticity

dv_dH

(ii)

(3) The stream function (incompressible flow) ip describes a continuous flow in two dimensions where the velocity at any point is given by

dip dx

(iii)

(4) The velocity potential ф describes an irrotational flow in two dimensions where the velocity at any point is given by

дф дф

“ = а~х У = Щ (,v)

Substituting (iii) in (i) gives the identity

d2ip d2ip

dxdy ~ dxdy ~

which demonstrates the validity of (iii), while substituting (iv) in (ii) gives the identity

д2ф д2ф

dxdy dxdy

demonstrating the validity of (iv), i. e. a flow described by a unique velocity potential must be irrotational.

Alternatively substituting (iii) in (ii) and (iv) in (i) the criteria for irrotational continuous flow are that

д2ф д2ф _ д2Ф д2,ф д7- + д?= = ~дх2+Ъу2

also written as Х72ф = Х72ф — 0, where the operator nabla squared

92 d2 dx2 + dy2

Eqn (3.4) is Laplace’s equation.

Consider a point P having a velocity potential ф (ф is the integral of the flow component along OP) and let another point Pi close to P have the same velocity potential ф. This then means that the integral of flow along OPi equals the integral of flow along OP (Fig. 3.3). But by definition OPPi is another path of integration from О to Pi. Therefore

Fig. 3.3 but since the integral along OP equals that along OPi there can be no flow along the remaining portions of the path of the third integral, that is along PP^ Similarly for other points such as P2, P3, having the same velocity potential, there can be no flow along the line joining Pj to P2.

The line joining P, Pi, P2, P3 is a line joining points having the same velocity potential and is called an equipotential or a line of constant velocity potential, i. e. a line of constant ф. The significant characteristic of an equipotential is that there is no flow along such a line. Notice the correspondence between an equipotential and a streamline that is a line across which there is no flow.

The flow in the region of points P and Pi should be investigated more closely. From the above there can be no flow along the line PPb but there is fluid flowing in this region so it must be flowing in such a way that there is no component of velocity in the direction PPi. So the flow can only be at right-angles to PPb that is the flow in the region PPi must be normal to PPi. Now the streamline in this region, the line to which the flow is tangential, must also be at right-angles to PPi which is itself the local equipotential.

This relation applies at all points in a homogeneous continuous fluid and can be stated thus: streamlines and equipotentials meet orthogonally, i. e. always at right – angles. It follows from this statement that for a given streamline pattern there is a unique equipotential pattern for which the equipotentials are everywhere normal to the streamlines.

The stream function (see Section 2.5) at a point has been defined as the quantity of fluid moving across some convenient imaginary line in the flow pattern, and lines of constant stream function (amount of flow or flux) may be plotted to give a picture of the flow pattern (see Section 2.5). Another mathematical definition, giving a different pattern of curves, can be obtained for the same flow system. In this case an expression giving the amount of flow along the convenient imaginary line is found.

In a general two-dimensional fluid flow, consider any (imaginary) line OP joining the origin of a pair of axes to the point P(jc, y). Again, the axes and this line do not impede the flow, and are used only to form a reference datum. At a point Q on the line let the local velocity q meet the line OP in /3 (Fig. 3.1). Then the component of velocity parallel to 8s is q cos /3. The amount of fluid flowing along 8s is q cos /3 8s. The total amount of fluid flowing along the line towards P is the sum of all such amounts and is given mathematically as the integral f q cos /3 ds. This function is called the velocity potential of P with respect to О and is denoted by ф.

Now OQP can be any line between О and P and a necessary condition for Jq cos /3dy to be the velocity potential ф is that the value of ф is unique for the point P, irrespective of the path of integration. Then:

(3.1)

If this were not the case, and integrating the tangential flow component from О to P via A (Fig. 3.2) did not produce the same magnitude of ф as integrating from О to P

Fig. 3.1

Fig. 3.2

via some other path such as B, there would be some flow components circulating in the circuit OAPBO. This in turn would imply that the fluid within the circuit possessed vorticity. The existence of a velocity potential must therefore imply zero vorticity in the flow, or in other words, a flow without circulation (see Section 2.7.7), i. e. an irrotational flow. Such flows are also called potential flows.

Sign convention for velocity potential

The tangential flow along a curve is the product of the local velocity component and the elementary length of the curve. Now, if the velocity component is in the direction of integration, it is considered a positive increment of the velocity potential.

Preamble

The aim of this chapter is to describe methods for calculating the air flow around various shapes of body. The classical assumption of irrotational flow is made, meaning that the vorticity is everywhere zero. This also implies inviscid flow. Irrotational flows are potential fields. A potential function, known as the velocity potential, is introduced. It is shown how the velocity components can be determined from the velocity potential. The equations of motion for irrotational flow reduce to a single partial differential equation for velocity potential known as the Laplace equation. Classical analytical techniques are described for obtaining two-dimensional and axisymmetric solutions to the Laplace equation for aerodynamic applications. The chapter ends by showing how these classical analytical solutions can be used to develop computational methods for predicting the potential flows around the complex three­dimensional geometries typical of modern aircraft.

3.1 Introduction

The concept of irrotational flow is introduced briefly in Section 2.7.6. By definition the vorticity is everywhere zero for such flows. This does not immediately seem a very significant simplification. But it turns out that zero vorticity implies the existence of a potential field (analogous to gravitational and electric fields). In aerodynamics the main variable of the potential field is known as the velocity potential (it is analogous to voltage in electric fields). And another name for irrotational flow is potential flow. For such flows the equations of motion reduce to a single partial differential equa­tion, the famous Laplace equation, for velocity potential. There are well-known techniques (see Sections 3.3 and 3.4) for finding analytical solutions to Laplace’s equation that can be applied to aerodynamics. These analytical techniques can also be used to develop sophisticated computational methods that can calculate the potential flows around the complex three-dimensional geometries typical of modern aircraft (see Section 3.5).

In Section 2.7.6 it was explained that the existence of vorticity is associated with the effects of viscosity. It therefore follows that approximating a real flow by a potential flow is tantamount to ignoring viscous effects. Accordingly, since all real fluids are viscous, it is natural to ask whether there is any practical advantage in

studying potential flows. Were we interested only in bluff bodies like circular cylin­ders there would indeed be little point in studying potential flow, since no matter how high the Reynolds number, the real flow around a circular cylinder never looks anything like the potential flow. (But that is not to say that there is no point in studying potential flow around a circular cylinder. In fact, the study of potential flow around a rotating cylinder led to the profound Kutta-Zhukovski theorem that links lift to circulation for all cross-sectional shapes.) But potential flow really comes into its own for slender or streamlined bodies at low angles of incidence. In such cases the boundary layer remains attached until it reaches the trailing edge or extreme rear of the body. Under these circumstances a wide low-pressure wake does not form, unlike a circular cylinder. Thus the flow more or less follows the shape of the body and the main viscous effect is the generation of skin-friction drag plus a much smaller component of form drag.

Potential flow is certainly useful for predicting the flow around fuselages and other non-lifting bodies. But what about the much more interesting case of lifting bodies like wings? Fortunately, almost all practical wings are slender bodies. Even so there is a major snag. The generation of lift implies the existence of circulation. And circul­ation is created by viscous effects. Happily, potential flow was rescued by an important insight known as the Kutta condition. It was realized that the most important effect of viscosity for lifting bodies is to make the flow leave smoothly from the trailing edge. This can be ensured within the confines of potential flow by conceptually placing one or more (potential) vortices within the contour of the wing or aerofoil and adjusting the strength so as to generate just enough circulation to satisfy the Kutta condition. The theory of lift, i. e. the modification of potential flow so that it becomes a suitable model for predicting lift-generating flows is described in Chapters 4 and 5.

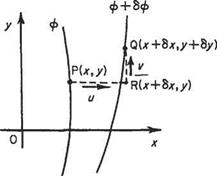
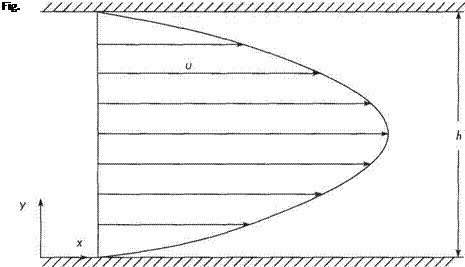
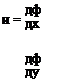The simplest example of this type of flow, illustrated in Fig. 2.32, is generated by uniform flow impinging perpendicularly on an infinite plane. The flow divides equally about a stagnation point (strictly a line). The velocity field for the corresponding inviscid potential flow (see Chapter 3) is

и = ax v = —ay where a is a const. (2.111)

The real viscous flow must satisfy the no-slip condition at the wall – as shown in Fig. 2.32 – but the potential flow may offer some hints on seeking the full viscous solution.

This special solution is of particular interest for aerodynamics. All two­dimensional stagnation flows behave in a similar way near the stagnation point. It can therefore be used as the starting solution for boundary-layer calculations in the case of two-dimensional bodies with rounded noses or leading edges (see Example 2.4). There is also an equivalent axisymmetric stagnation flow.

The approach used to find a solution to the two-dimensional Navier-Stokes Eqns (2.92) and (2.93) is to aim to reduce the equations to an ordinary differential equation. This is done by assuming that, when appropriately scaled, the non-dimensional

Fig. 2.32 Stagnation-zone flow field velocity profile remains the same shape throughout the flow field. Thus the nature of the flow field suggests that the normal velocity component is independent of x, so that

v = -/00 (2-112)

where f(y) is a function of у that has to be determined. Substitution of Eqn (2.112) into the continuity Eqn (2.93) gives

= /’ O’) і integrate to get и = xf{y) (2.113)

where ()’ denotes differentiation with respect to y. The constant of integration in Eqn (2.113) is equivalently zero, as u — v — 0 at x = 0 (the stagnation point), and was therefore omitted.

For a potential flow the Bernoulli equation gives

P + ^p(j£+_£) =Po – (2-114)

a2*2+o2.y2

So for the full viscous solution we will try the form:

Po-P = p^[^ + f(y)], (2.115)

where F(y) is another function of y. If the assumptions (2.112) and (2.115) are incorrect, we will fail in our objective of reducing the Navier-Stokes equations to ordinary differential equations.

Simplifying these two equations gives

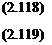
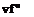
/2 _//" = a2 + vfn 1

In its present form Eqn (2.118) contains both a and v, so that / depends on these parameters as well as being a function of y. It is desirable to derive a universal form of Eqn (2.118), so that we only need to solve it once and for all. We attempt to achieve this by scaling the variables /(y) and y, i. e. by writing

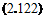f{y) = 0ф(т]), 77 = ay

where a and /3 are constants to be determined by substituting Eqn (2.122) into Eqn (2.118). Noting that

d/ drj йф,

/=5TdA; *

Eqn (2.118) thereby becomes

а2(32фа – а2(32фф" = a2 + (2.123)

Thus providing

a2 ft2 = a2 = va3 в, implying a = /a/v, /3 = fav (2.124)

they can be cancelled as common factors and Eqn (2.124) reduces to the universal form:

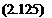ф’" + фф"-ф’2 + 1=0

with boundary conditions

0(0) = Ф'( 0) = 0, ф'( oo) = 1

In fact, ф’ = u! Ue where Ue = ax the velocity in the corresponding potential flow found when 77 —> oc. It is plotted in Fig. 2.33. We can regard the point at which ф’ = 0.99 as marking the edge of the viscous region. This occurs at 77 ~ 2.4. This viscous region can be regarded as the boundary layer in the vicinity of the stagnation point (note, though, no approximation was made to obtain the solution). Its thick­ness does not vary with x and is given by

4.0
3.5
3.0
2.5
n 2.0
1.5
1.0
0.5

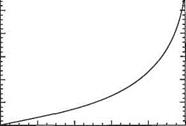
Fig. 2.33

Example 2.4 Calculating the boundary-layer thickness in the stagnation zone at the leading edge.

We will estimate the boundary-layer thickness in the stagnation zone of (i) a circular cylinder of 120 mm diameter in a wind-tunnel at a flow speed of 20m/s; and (ii) the leading-edge of a Boeing 747 wing with a leading-edge radius of 150 mm at a flight speed of 250 m/s.

For a circular cylinder the potential-flow solution for the tangential velocity at the surface is given by 2UX sin ф (see Eqn (3.44)). Therefore in Case (i) in the stagnation zone, x = R sin ф ~ Кф, so the velocity tangential to the cylinder is

Ut a 2ихф = 2% Rф

JV

X

Therefore, as shown in Fig. 2.34, if we draw an analogy with the analysis in Section 2.10.3 above, a = 21/oJR = 2 x 20/0.06 = 666.7 sec-1. Thus from Eqn (2.126), given that for air the kinematic viscosity, v ~ 15 x 10-6 m[7]/s,

For the aircraft wing in Case (ii) we regard the leading edge as analogous locally to a circular cylinder and follow the same procedure as for Case (i). Thus R = 150 mm = 0.15 m and U0о = 250m/s, so in the stagnation zone, a = 2UaJR = 2 x 250/0.15 = 3330sec-1 and

These results underline just how thin the boundary layer is! A point that will be taken up in Chapter 7.

Fig. 2.34

Exercises

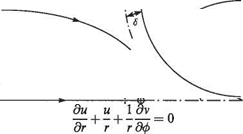
1 Continuity Equation for axisymmetric flow

(a) Consider an axisymmetric flow field expressed in terms of the cylindrical coordinate system (г, <f>, z) where all flow variables are independent of the azimuthal angle ф. For example, the axial flow over a body of revolution. If the velocity components (m, w) correspond to the coordinate directions (r, z) respectively, show that the continuity equation is given by

(b) Show that the continuity equation can be automatically satisfied by a stream – function ф of a form such that

(b) Show that the continuity equation can be automatically satisfied by a stream- function ф of a form such that

3

Transport equation for contaminant in two-dimensional flow field In many engineering applications one is interested in the transport of a contaminant by the fluid flow. The contaminant could be anything from a polluting chemical to particulate matter. To derive the governing equation one needs to recognize that, provided that the contaminant is not being created within the flow field, then the mass of contaminant is conserved. The contaminant matter can be transported by two distinct physical mechanisms, namely convection and molecular diffusion. Let C be the concentration of contaminant (i. e. mass per unit volume of fluid), then the rate of transport of contamination per unit area is given by

where і and j are the unit vectors in the x and у directions respectively, and T> is the diffusion coefficient (units m2js, the same as kinematic viscosity).

Note that diffusion transports the contaminant down the concentration gradient (i. e. the transport is from a higher to a lower concentration) hence the minus sign. It is analogous to thermal conduction.

(a) Consider an infinitesimal rectangular control volume. Assume that no contam­inant is produced within the control volume and that the contaminant is sufficiently dilute to leave the fluid flow unchanged. By considering a mass balance for the control volume, show that the transport equation for a contaminant in a two­dimensional flow field is given by

(b) Why is it necessary to assume a dilute suspension of contaminant? What form would the transport equation take if this assumption were not made? Finally, how could the equation be modified to take account of the contaminant being produced by a chemical reaction at the rate of mc per unit volume.

4 Euler equations for axisymmetric flow

(a) for the flow field and coordinate system of Ex. 1 show that the Euler equations (inviscid momentum equations) take the form:

5 The Navier-Stokes equations for two-dimensional axisymmetric flow

(a) Show that the strain rates and vorticity for an axisymmetric viscous flow like that

described in Ex. 1 are given by:

[Hint: Note that the azimuthal strain rate is not zero. The easiest way to determine it is to recognize that in + ёфф + izz = 0 must be equivalent to the continuity equation.]

(b) Hence show that the Navier-Stokes equations for axisymmetric flow are given by /du du ди dp /cP’u Іди и д2u

рді + ид? + кЫ=Р8г~Ъ? + рд^ + ~г’дг~^ + Ъ?)

/dw dw dw dp /d^w 1 dw d2w

РШ + u^ + wfc)=p8z-fc + pd*+7fr + d*)

6 Euler equations for two-dimensional flow in polar coordinates

(a) For the two-dimensional flow described in Ex. 2 show that the Euler equations

(inviscid momentum equations) take the form:

[Hints: (i) The momentum components perpendicular to and entering and leaving the side faces of the elemental control volume have small components in the radial direction that must be taken into account; likewise (ii) the pressure forces acting on these faces have small radial components.]

7 Show that the strain rates and vorticity for the flow and coordinate system of Ex. 6 are given by:

. _ du. _ 1 dv и

= Єфф = ~гдф + ~г

. _ 1 (®v v 1 ®u c _ 1 5v v

1гф = 2 дг~~г+~гдфГ ^ = ^дф~д? + г

[Hint: (і) The angle of distortion (/3) of the side face must be defined relative to the line joining the origin О to the centre of the infinitesimal control volume.]

8 (a) The flow in the narrow gap (of width A) between two concentric cylinders of length L with the inner one of radius R rotating at angular speed и can be approximated by the Couette solution to the Navier-Stokes equations. Hence show that the torque T and power P required to rotate the shaft at a rotational speed of wrad/s are given by

2npu>R3L Ітціш2 R? L

T= A ’ P = A

9 Axisymmetric stagnation-point flow

Carry out a similar analysis to that described in Section 2.10.3 using the axisymmetric form of the Navier-Stokes equations given in Ex. 5 for axisymmetric stagnation – point flow and show that the equivalent to Eqn (2.118) is

ф’" + 2 фф" – фа + 1=0

where ф’ denotes differentiation with respect to the independent variable ( = sjajvz and ф is defined in exactly the same way as for the two-dimensional case.

This also corresponds to the flow between two infinite, plane, parallel surfaces (see Fig. 2.31). Unlike Couette flow, both surfaces are stationary and flow is produced by the application of pressure. Thus all the arguments used in Section 2.10.1 to simplify the Navier-Stokes equations still hold. The only difference is that the pressure term in Eqn (2.95a) is retained so that it simplifies to

“ё+’*|г=0 implyi, Ig “_^+Ciy+C2 <2108)

The no-slip condition implies that и = 0 at у = 0 and h, so Eqn (2.108) becomes

–ШО-0 (210,)

Thus the velocity profile is parabolic in shape.

The true Poiseuille flow is found in capillaries with round sections. A very similar solution can be found for this case in a similar way to Eqn (2.109) that again has
a parabolic velocity profile. From this solution, Poiseuille’s law can be derived linking the flow rate, Q, through a capillary of diameter d to the pressure gradient, namely

7rd4 dp 128/i dx

Poiseuille was a French physician who derived his law in 1841 in the course of his studies on blood flow. His law is the basis of another type of viscometer whereby the flow rate driven through a capillary by a known pressure difference is measured. The value of viscosity can be determined from this measurement by using Eqn (2.110).