Category Aircraft Flight

If a fuselage is now added to the wing we have basically the same problems which occurred on the isolated wing from the point of view of correcting the local load distribution, but we now also have to superimpose the flow pro­duced by the fuselage.

In isolation the fuselage will speed up the local air stream as it flows past, and that is precisely what happens to the local air stream at the wing centre section when the fuselage is added. This means that the local Mach number on the wing will be increased, thus adding to the possibility of locally strong shock waves being formed. The detailed flow in the junction between the wing and fuselage can be very complicated, and in general acute angles are best avoided. This leads to the conclusion that a centre-mounted wing is likely to be the best bet. However this solution is not desirable in such designs as transport aircraft, where a clear fuselage is essential. Indeed whether the wing is mounted low or high may be decided by such factors as ground engine clearance or under­carriage length rather than by pure aerodynamic considerations.

If, however, we are faced with a situation in which there is some choice over the fuselage geometry and we are not simply restricted to using a straight tube, we find that we have another design parameter at our disposal. As well as modifying the local flow at the wing centre section by changes in the shape of the wing itself, we can also change the flow by modifying the local cross­sectional shape of the fuselage in order to make the local streamlines follow the shape they would adopt on the infinite wing. Alternatively, if the basic form of the fuselage must remain unaltered, a suitable fillet can be used at the wing/fuselage junction.

In the previous chapter, in Fig. 10.1, we defined the three turning motions; pitch, yaw and roll. Pitching stability (nose-up/nose-down motion) is known as longitudinal stability.

Lateral stability is a term used rather loosely to refer to both rolling and yawing. These two motions are very closely interconnected, as we noted when describing control surfaces.

Fortunately, the coupling between longitudinal and lateral static stability is normally weak, and for the purposes of our simple introduction, it is conveni­ent to treat them separately. This again, was part of the traditional approach. It should be noted, however, that in highly manoeuvrable aircraft, the cross­coupling can be significant.

Longitudinal static stability

Aerofoil centre of pressure and aerodynamic centre

For an aerofoil, the point along the chordline through which the resultant lift force is acting, is known as the centre of lift, or centre of pressure. On a cam­bered aerofoil, the centre of pressure moves forward with increasing angle of attack, as shown in Fig. 11.2(a).

When a cambered aerofoil is set at an angle of attack where it produces no lift, we find that it still gives a nose-down pitching moment. Since there is no force, this moment must be a pure couple. Figure 11.3 shows how this arises physically. The downforce on the front of the aerofoil is balanced by an upward force at the rear, so there is no net force, but a couple is produced.

It is a surprising feature of aerofoils that there is one position on the chord line where the magnitude of this pitching moment does not change significantly with varying angle of attack. Therefore, as illustrated in Fig. 11.2(b), we can represent the forces on an aerofoil as being a combination of a couple and a lift force (L) acting through that position. The position is known as the aero­dynamic centre. It is useful to have such a fixed reference point, because, as the angle of attack reduces towards zero, the centre of pressure moves further and further aft, eventually disappearing off towards infinity.

The above description perhaps gives a deceptively simple view of the landing procedure. Flying an accurate approach is a very demanding exercise and there is more than one way of going about it, the choice being determined by the aircraft type and pilot preference. The term ‘glide path’ for this part of the landing is somewhat misleading. It is perfectly possible to fly this part of the approach with the engine idling and this was a popular method some years ago.

With a gas-turbine engine in particular, the safer method is to fly down the glide path using a significant amount of power with the aircraft flaps being

used to provide a high drag setting. This procedure gives better control. The throttle setting can be decreased as well as increased, the latter being the only option available in the true gliding approach. Even more important is the fact that a gas turbine engine is very slow to pick up from idling speed when the throttle is suddenly opened. It is therefore a safer procedure to fly the approach under power to facilitate recovery from an aborted landing. The improved control afforded by this procedure has, however, led to its wide adoption even for light piston-engined aircraft.

Assuming that the pilot has broadly got the aircraft set up at the correct angle of attack and throttle setting to follow the required glide path, there will inevitably be small corrections needed from time to time. Here again the pilot has some choice in the matter. Provided the aircraft is not dangerously near the stall, such corrections can be made by controlling the aircraft angle of attack by elevator movement. This will result in some change in speed as well as glide angle. The alternative is to change the throttle setting and for piston-engined aircraft this method is frequently preferred because of the smaller change in speed. For jet aircraft and especially large ones, the former method is frequently used. This is because of the slow response of the engine, which makes accurate correction difficult. Further, if the aircraft is heavy, it will take a long time for the speed to change, which minimises the main dis­advantage of the method.

When flying down the glide path the pilot must have some means of check­ing that he is flying to the correct glide slope. Nowadays a variety of aids are available, and some of these are discussed below. In the absence of more complex aids he will need some reference markers, which may be simple radio beacons, at known distances from the runway threshold. He can check the height on the altimeter on passing these markers and estimate the required descent rate appropriate to the speed of the aircraft. In order to help to the correct descent rate the aircraft is fitted with a Vertical Speed Indicator (VSI) which works by sensing the rate of change of atmospheric pressure as the aircraft descends.

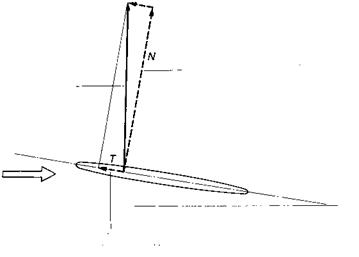
It is often incorrectly thought, that the resultant force due to the pressure acts more or less at right angles to the plane of the wing. However, referring to Fig. 1.16, it may be seen that in addition to a perpendicular or normal force component N, produced by the difference in pressure between upper and lower surfaces, there is also a tangential component T, produced as a consequence of the low pressure acting on the leading edge. This ties in with theory which indicates that in the absence of three-dimensional effects, and as long as the flow follows the contours of the aerofoil, the lift force should be at right angles to the direction of the main air stream, and not at right angles to the plane of the wing.

Even when the wing is virtually a flat plate with a small leading edge area, as in Fig. 1.16, the very low pressure acting on it results in a significant forward force. If the plate is very thin, then the air simply fails to follow the contours of the surface at anything other than very small angles of attack, and the amount of lift generated is relatively small. In this case the resultant force is more or less at right angles to the plate.

The resultant aerodynamic force is never quite at right angles to the free – stream direction in practice, as there is always a rearward drag component due to friction caused by the influence of the viscosity of the air.

Force due to difference in pressures

between upper and lower surfaces

Force due to difference in pressure between leading and trailing faces

Fig. 1.16 The direction of the resultant force due to pressure

As long as the flow follows the contours of the section, there is a small tangential component of force resulting from the low pressure on the leading edge

Lift coefficient

The amount of lift produced by a wing depends on its plan area, the density of the air, the flight speed, and a factor that we call the lift coefficient (CL). The relationship can be expressed by

Lift = 2pV 2SCl

where S represents the wing plan area, p is the density, and V is the speed. You will see that the dynamic pressure (-pV2) occurs in this expression, and that, as mentioned earlier, the lift force is directly related to it.

The lift coefficient CL may be thought of as being a measure of the lifting effectiveness of the wing, and depends mainly on the wing geometry; that is, on the section shape, planform and angle of attack. CL also depends on the compressibility and the viscosity of the air, but for the time being, it will be convenient to ignore these latter influences.

The lift coefficient depends mainly on the shape of the wing, and is only relatively weakly dependent on its size. This is extremely convenient, because we can measure CL quite easily using a model in a wind tunnel, and with the aid of the above expression, we can calculate the amount of lift that would be produced by any size of wing at any required combination of speed and air density.

A further advantage is that for the whole range of flying conditions, the variation of lift with angle of attack can be calculated by using a single graph of CL plotted against angle of attack.

Unfortunately, when accurate predictions are required, the influences of viscosity and compressibility mentioned above, have to be allowed for, and the procedure can become much more complicated.

Another useful feature of CL, is that it is a dimensionless quantity (like a ratio), which means that it has the same numerical value, regardless of what system of units is used (e. g. Imperial or SI).

Sometimes, a separated flow will reattach, as illustrated in Fig. 3.4. This is particularly likely to happen if the boundary layer was laminar when it separ­ated. After separation, the layer tends to become turbulent and thus more able to tolerate an adverse pressure gradient.

Between the points of separation and reattachment, a region of recirculating air, known as a separation bubble, is formed, as shown in Fig. 3.4. Many aero­foils show a tendency to produce such a bubble. The lifting properties are not affected, as long as the bubble is sustained.

Differences between high and low speed flows

Sound waves consist of a succession of weak pressure disturbances which pro­pagate through the air. The speed at which these disturbances advance through the air is called the speed of sound, and we find that this speed is of great significance in aerodynamics. The speed of sound is not constant but depends upon the square root of the absolute air temperature. Thus, at low altitudes, where the temperature is relatively high, the speed of sound is higher than it is at high altitudes where the temperature is less (see Chapter 7).

Figure 5.1 shows the difference between the flows over a simple aerofoil on an aircraft flying at (a) a speed below the speed of sound (subsonic) and

(b) a speed greater than the speed of sound (supersonic). A number of signi­ficant differences are apparent. Firstly in the low speed flow the air is disturbed a long way in front of the aerofoil, while, for the supersonic flow, the area of disturbance is strictly limited and ahead of this region the air is totally un­affected by the presence of the aerofoil. Secondly, the local direction of the flow varies relatively smoothly at the low speed, while at high speed there is a very abrupt change where the air is first disturbed.

More detailed examination of the flow also shows that there are cor­respondingly abrupt changes in speed, temperature and pressure along a streamline. The line along which these abrupt changes take place is known as a shock wave. As can be seen in Fig. 5.1, shock waves form both at the leading and trailing edges of our aerofoil. The formation of shock waves is of great importance in high speed flow and we shall be looking at them in greater detail shortly.

The power output of a piston engine can be considerably increased by using a supercharger to pressurise the air being fed into the cylinders, so that a larger mass of air is used in each working stroke. The use of a supercharger can, there­fore, improve the engine’s power-to-weight ratio.

An important advantage of a supercharger is that it enables an engine to operate at higher altitude than it could in normally aspirated (un-supercharged) form. As the altitude increases, the air density falls, and without supercharg­ing the mass of air taken in per working stroke would fall. Since there is less oxygen, less fuel can be burned, and there is a consequent loss of power.

The supercharger enables an aircraft to take off heavily laden from high altitude airfields on hot days. By cruising at high altitude, the aircraft may also sometimes be able to take advantage of strong tail winds.

A supercharger usually consists of a centrifugal compressor driven from the crankshaft. A turbocharger is similar to a supercharger, except that the com­pressor is driven by a turbine, which is powered by the residual energy in the exhaust gases. Unlike the supercharger, the speed of the turbocharger is, there­fore, not directly related to the engine speed. Because it makes use of otherwise wasted heat, the turbocharger is inherently more efficient than a plain super­charger, and has become the type normally used. Both devices can roughly double the power output for a given size and weight of engine.

For small aircraft, the disadvantage of turbocharging is that it adds to the cost and complication of the engine, and the boost pressure is yet another vari­able that the pilot has to monitor or control. There is little advantage in using a turbocharger, unless the pilot is able to take advantage of the benefits of high altitude operation. This in turn means that either the aircraft must be pres­surised, or an oxygen mask and supply system must be provided. Civil aviation regulations require that for high altitude operation, additional instruments, navigation and communication equipment must be installed, and the pilot must be suitably qualified to use them. In recent years, a number of pressurised turbocharged light aircraft have appeared, such as the Cessna Centurion. Garrison (1981) gives a good description of the pros and cons of turbocharged light aircraft.

The purpose of an aircraft is not always to transport people or cargoes between two locations, sometimes the aircraft is used as a radar or visual observation platform, and in this case the main design consideration will be the length of time it can remain airborne, or its endurance.

In this case we require, not the minimum fuel flow over a given distance, but the minimum fuel flow in unit time. Here we will adopt the same approach as before and look at the airframe from an idealised point of view to get an initial idea of the way things behave. Following this we will look at the real engine behaviour to get a more accurate picture of the operational requirements of the complete aircraft.

If we take an initial guess, we would suppose that the best way to operate the airframe for maximum endurance would be to fly at the condition at which the smallest amount of work needs to be expended in unit time in order to overcome the drag force. The rate at which work is done is equal to power, so this operating point is equivalent to the flying speed and cor­responding aircraft attitude which results in minimum power, rather than minimum drag.

Because we are now concerned with power, rather than drag, we will con­sider the power required by the airframe and powerplant and plot them in a similar manner to the drag curves of Fig. 7.4. The power required curve is very easily derived from the drag curve. All we have to do is multiply each value of the drag by the speed at which it occurs and replot as in Fig. 7.10. Then we superimpose the power, rather than the thrust, curve for the particular power – plant we are using.

We find that the power reaches a minimum value at a speed slightly lower than the minimum drag speed. In constructing the power curves we must again remember that we are talking about an aircraft flying straight and level at a constant weight.

Now we have decided what the airframe is doing, we will take a simpli­fied look at the compromise which must be reached for the different power plant types, as we did when considering how to operate for best economy and range.

In a tail-first or canard (the French word for a duck) configuration, shown in Fig. 10.8, and Fig. 10.1, a nose-up pitching moment is obtained by using the forward foreplane to lift the nose up. Rotating the foreplane surface to increase its incidence will increase its lift and consequently the overall lift.

Operating the elevator control on a canard configuration produces an immediate increase in lift, and thus, a more favourable response to pitch con­trol. Together with other factors described later, this has led to the adoption of

a canard configuration on many aircraft, particularly delta-winged types, as illustrated in Fig. 10.8, where a slab-type canard foreplane may be seen. The foreplane is capable of a large range of movement.

The experimental X-29, shown in Fig. 9.20, has no fewer than three sets of pitch-control surfaces, resulting in something of a headache for the control system designer.

In the simple cases shown in Figs 11.5 and 11.6 we conveniently had the drag force passing through the centre of gravity. In practice, the line of action of the tailplane drag must move as the aircraft attitude changes. With the aid of sim­ple sketches, it is easy to work out that for a conventional aircraft this produces a stabilising tendency, while for a canard, the influence is destabilising.

In addition to the factors given above, we also have to consider the influence of fuselage, flaps, undercarriage, external stores (armaments) and any other features that can produce either an aerodynamic force or moment, or a change in the centre of gravity position. It is also very important to take account of the flexibility of the aircraft and control system components.