Category Aircraft Flight

As with lift, it is convenient to refer to a drag coefficient CD defined, in a sim­ilar way to lift coefficient, by

Drag = Dynamic pressure x wing area x CD or D = pV2 x S x CD

where S is the wing plan area.

For an aircraft, a major contribution to the overall drag comes from the wing, and is largely dependent on the plan area. We therefore wish to find ways of minimising the drag for a given wing plan area, and it is sensible to relate CD to the plan area, as in the expression above. Note, however, that for cars, CD is based on the frontal area. Drag coefficient values for cars cannot, therefore, be compared directly with values for aircraft. The drag coefficient of missiles is also normally based on the body frontal area.

The wing drag coefficient depends on the angle of attack, the Reynolds num­ber (air density x speed x mean wing chord/viscosity coefficient), and on the Mach number (speed/speed of sound). For many shapes, the dependence of CD on Reynolds number is weak over a wide range, and for simple estimations, the dependence on Reynolds number is often ignored. For speeds up to about half the speed of sound, the variation with Mach number is normally negligible, and so, for early low speed aircraft, it was customary to treat CD as being dependent only on the angle of attack and geometric shape of the aircraft. However, as we described in the last chapter, ignoring the effects of Reynolds number can lead to serious errors. For high speed aircraft, the effect of Mach number becomes extremely important.

The change in the speed of the air between inlet and outlet means that its momentum has been increased, so thrust is obviously produced, but where? At first sight, air flowing through a hollow tube might be expected to produce nothing more than friction drag. In fact, the thrust force is mainly produced by pressure differences between rearward-facing and forward-facing surfaces. In Fig. 6.2, the contributions to thrust and drag of a typical jet engine are shown. Note how the net output thrust is only a small proportion of the total thrust produced internally, indicating that there are very large internal stresses. The case shown relates to a stationary engine. In flight, much of the thrust may come from the pressure distribution in the intake duct system.

The actual distribution of forces in and around the engine varies with its design and the operating conditions. There are many contributions, and it is no simple matter to assess them all accurately. However, we can conveniently measure the total thrust by determining the overall momentum change and pressure difference across the engine.

The overall net thrust is partly related to the air flow round the outside of the engine. The external flow mostly produces drag, but round the leading edge (the
rim) of the intake, the flow speed is high, so the pressure is low, and under some conditions this may produce a significant forward thrust component. The aero­dynamic design of the intake, ducting and engine nacelle is thus very important.

When air enters the intake of a jet engine, its speed is reduced, and the pressure rises correspondingly. This ram compression effect means that as the aircraft speed rises, the compressor becomes less and less necessary. At Mach numbers in excess of about 3 (three times the speed of sound), efficient propulsion can be obtained with no compressor at all. Elimination of the compressor means that the turbine is also unnecessary. All that is required is a suitably shaped duct with a combustion chamber. This extremely simple form of jet propulsion is known as a ramjet.

The basic principle of the ramjet is illustrated in Fig. 6.37. The thrust force is produced mainly by a high pressure acting on the interior walls of the intake. For efficient operation at high Mach numbers, a more complicated intake geometry is required; similar to the types used for the supersonic turbo-jet propulsion, as described above.

The problem with ramjets is that they are inefficient below a Mach number of about 3, and will not work at all if there is no forward motion. Some other form of propulsion is required to provide the initial acceleration to high speed. In the case of missiles, an initial booster rocket is normally used. In the early postwar era, the French Leduc company produced a number of ramjet-propelled experimental aircraft which flew successfully (Fig. 6.38). They were normally flight-launched from a mother aircraft, and landed as gliders.

At very high Mach numbers, it becomes necessary to have supersonic flow in the combustion area. This is known as a scramjet (supersonic combusting ramjet) propulsion. Conventional combustion systems that simply involve adding fuels such as kerosene to the air flow cannot be used, as the flame would not propagate as fast as the flow, and it would thus simply blow out. The unmanned X-43A hypersonic research aircraft powered by a scramjet engine is described in Chapter 8, and shown in Fig. 8.24.

The dual-mode turbo-ramjet

As an alternative to air launching or a booster engine, some form of dual – or multi-mode propulsion may be used. One approach is to use a turbo-jet engine inside a ramjet duct, as illustrated in Fig. 6.39. At low speeds, the engine per­forms as a conventional turbo-jet. At high Mach numbers, however, some or all of the air may be by-passed around the main core engine and used in an afterburner to produce ramjet propulsion.

The advantage of this arrangement over a conventional turbo-jet is that the ramjet becomes more efficient at high Mach numbers, because the energy degradation in the turbine and compressor is eliminated. The SR-71 shown in Fig. 6.40 uses a form of turbo-ramjet propulsion.

Unfortunately, at the Mach number where ramjet propulsion becomes efficient, kinetic heating effects render conventional aluminium alloys and con­struction techniques unsuitable. Very few aircraft with a Mach 3 capability have been built, and most of these have been experimental or research vehicles. The SR-71 reconnaissance aircraft shown in Fig. 6.40 is a rare example of a production machine with Mach 3+ capability. This has now been withdrawn from active service.

Nozzle in

convergent

Primary n. – divergent

flow Coreengine configuration

Subsonic flow

Fig. 6.39 Schematic arrangement of a turbo-ramjet

At high supersonic speeds, the primary flow by-passes the core turbo-jet, and the afterburner is used to provide ramjet propulsion

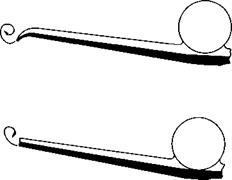
The central spike moves in and out axially to match the intake geometry to the flight conditions

For efficient operation, the spike shock wave should just strike the intake rim.

The spike is also moved when ‘starting’ the intake shock system

(a) Ramjet mode at high supersonic speed (b) Turbo-jet mode at subsonic speed

As the Mach number at which the aircraft flies is increased, so the sweep angle required to maintain a subsonic leading edge is also increased, and the problem of maintaining attached flow becomes more severe. However, we saw in Chap­ter 2 how a sharp leading edge could be used on a highly swept wing in order to give a well controlled separated flow with rolled up vortices situated above the top surface of the wing.

This type of separated vortex flow enables large angles of sweep to be employed for supersonic flight while at the same time providing accept­able low speed characteristics including reasonably good subsonic cruise capability. It is for these reasons that a configuration giving this type of flow was adopted for Concorde (Fig. 8.4) since extended fight at subsonic cruise is a requirement because of the restrictions on supersonic flight over populated areas.

In the case of the Concorde wing a supersonic trailing edge is employed, giv­ing the modified slender delta or ogive configuration. This has clear structural advantages and provides adequate wing area for low speed operation while at the same time producing the slender overall planform required for low bow shock strength in order to limit the wave drag. It does, however, involve the rearward movement in centre of lift referred to earlier as the aircraft acceler­ates from sub – to supersonic flight conditions. Normally this would lead to heavy aerodynamic penalties in providing the necessary trim adjustment, but as we have seen previously, the complex camber shape employed limits the centre of lift movement and the aerodynamic penalties are minimised by pumping fuel between fore and aft tanks as a trimming device.

The use of leading-edge vortex generation in supersonic swept wings may take a variety of forms. In the F-18 (Fig. 2.25) they are generated over only part of the leading edge by a very highly swept root section.

When an aircraft is banked (turned about the roll axis), the resulting forces produce a tendency to sideslip, as illustrated in Fig. 10.11. In sideslip motion, the fin produces a sideforce and hence a yawing moment, as shown in Fig. 10.11. Thus, banking an aircraft will cause it to turn towards the direction

Weight

Fig. 10.11 Sideslip and yaw due to roll

When an aircraft rolls, one component of weight acts sideways relative to the aircraft axes. This causes the aircraft to slip sideways. Once the sideslip develops, the fin will generate a sideforce tending both to right the aircraft and to yaw it towards the direction of the sideslip of the lower wing, unless compensated for by applying opposite rudder. This is another example of the cross-coupling between motions.

Mounting the wings well above the centre of gravity aids roll stability, but not for the reasons often assumed. Figure 11.16(a) shows a high-winged air­craft which is rolling, but has not yet developed a sideslip. It will be seen that both the lift and weight forces pass through the centre of gravity, so there is no restoring moment. The fuselage does not swing like a pendulum under the wing, as is often incorrectly believed. Once the sideslip commences as in Fig. 11.6(b) the wing becomes yawed to the resultant flow direction and the lower wing tends to generate increased lift due to the onset of vortical lift at the

tip. Also, the cross flow on the fuselage, due to sideslip, produces an upwash on the lower wing and a downwash on the upper wing. There may also be a slight sideways drag component. As illustrated, the resulting force no longer passes through the centre of gravity, and a restoring moment is produced. The lower the centre of gravity is, the greater will be the moment arm. Thus, high­winged aircraft do not need so much dihedral as low-wing types, and may even need none at all.

The use of wing sweep also enhances roll stability, as may be seen from Fig. 11.17. When a sideslip occurs, the lower wing presents a larger span as seen from the direction of the approaching air, and as with dihedral, the effect is to roll the aircraft back towards the horizontal.

Excessive rolling stability can produce undesirable dynamic instabilities due to cross-coupling between roll and yaw modes, such as in the Dutch roll described in Chapter 12. Swept-wing aircraft, therefore, often have negative dihedral, which is known as anhedral. Anhedral is often found on swept-winged aircraft that are also high-winged, as on the Antonov shown in Fig. 12.13.

Some of the practical implications of the relationships between speed and pres­sure are rather surprising at first sight. We might instinctively imagine that if air is squeezed through a converging duct, as illustrated in Fig. 1.10, the pres­sure would increase in the narrow part. At low speeds, this is not the case. If there are no leaks, then the same quantity of air per second must pass through the wide part as through the narrow part. Therefore, as the width of the duct decreases, the speed must increase. This increase in speed must be accompanied by a decrease in pressure. Thus, the pressure becomes lower as the duct nar­rows. We shall see later, however, that a different situation can occur when the flow speed approaches or exceeds the speed of sound.

Wing circulation

As we have stated, lift is produced as a consequence of the pressure difference between the upper and lower surfaces of the wing. This pressure difference is

related to the difference in the relative air speeds on the two surfaces, by the Bernoulli relationship given above. Hence, the amount of lift generated is related to the difference in relative speeds between upper and lower surfaces.

Referring to Fig. 1.11, we see that the speed of the air over any point on the upper surface can be considered as being a mean speed Vm plus a small com­ponent, whilst the speed of air flowing under the wing is Vm minus a small component.

From Fig. 1.11, we can see that the difference in the upper and lower surface air speeds is thus equivalent to adding, or superimposing, a rotational move­ment (indicated by the small black arrows) on to the average or mean motion at speed Vm (indicated by the dashed arrows).

Note that in this situation no individual particle of air actually travels around the profile in a complete circuit. The air flow may be thought of as merely having a circulatory tendency.

We measure the strength of the circulatory tendency by a quantity called the circulation; normally denoted by the letter K or the Greek letter Г. We will not concern ourselves here with an exact mathematical definition of circulation. In simple terms, increasing the circulation at a given flight speed, means increas­ing the difference in relative air flow speed between the upper and lower sur­faces, and hence, increasing the lift. The lift generated per metre of span is in fact equal to the product of the air density (p), the free-stream air speed (V), and the circulation (K).

L = pVK (per unit span).

Note that this means that the faster the flight speed (at a fixed altitude), the less will be the circulation required to generate a given amount of lift.

An interesting concept is the joined wing illustrated in Fig. 2.27. A forward – swept rear plane is joined at the tips to a rearward-swept main-plane. The

primary advantage of this concept is that if one wing is mounted low, and the other high, as shown, a stiff structure results. A potential additional advantage is that this arrangement produces a ‘non-planar’ lifting arrangement which can produce a relatively low drag, as explained in Chapter 4.