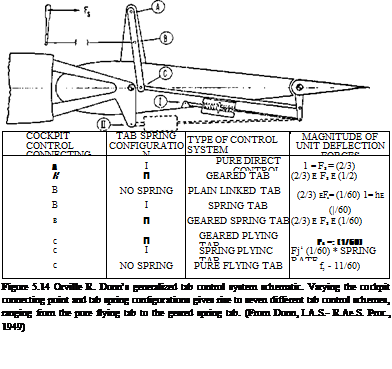
Thrust system dynamics reappeared as major problems many years after the Patuxent tests of the F8U and F4D-1 and the NACA, British RAE, and Systems Technology studies. Two carrier-based airplanes, the McDonnell Douglas/British Aerospace T-45A Goshawk and the Lockheed S-3A Viking, had similar problems (Wilson, 1992).
As a land-based trainer, the British Aerospace Hawk has a large speed brake or airbrake under the rear of the fuselage, aft of the wings, in the so-called ventral position. Extended, the speed brake would hit the ground when landing. The Hawk’s speed brake is thus designed to retract into the fuselage automatically when the landing gear is lowered. In common with many subsonic jet airplanes, the Hawk’s jet engine is the bypass variety. Bypass jet engines provide good low-airspeed performance, with high thrust levels, and they are fuel-efficient. However, high thrust at low airspeeds means that landing approaches are normally made at idle thrust settings, or low-engine RPM. Thus, if a go-around is required, a bit more time is needed to increase RPM to maximum than for an engine without bypass.
According to George Wilson’s account, U. S. Navy test pilot Captain George J. Webb, Jr., as a carrier suitability expert, flew the original Hawk airplane in November 1983 to evaluate its behavior in simulated carrier approaches. Quoting from a draft of a memorandum from Webb to Rear Admiral E. J. Hogan, Jr., commander of the Naval Air Test Center:
Glide slope tracking [with speed brake not extended] was difficult, and corrections from high, low, and off speed conditions often resulted in numerous glide slope overshoots. Use of the ventral speed brake improved glide slope tracking and made any necessary corrections easier to accomplish.
Aircraft attitude changes associated with speed corrections were very small and difficult to discern. The combined effect made it difficult for the pilot to recognize an underpowered, decelerating situation sufficiently early to make timely corrections. Consequently, student pilots will occasionally land hard or short of the runway during syllabus flights not monitored by an LSO [Landing Signal Officer].
It was thought that the T-45A would be a straightforward conversion to naval use of a simple, existing training airplane. Thus, full-scale engineering development leading to production of 300 airplanes was launched in 1984, concurrently with U. S. Navy flight tests of the Hawk, rather than after these had been completed. Some four years later, a first interim report on the McDonnell Douglas version, the T-45A, reported that the British Hawk landing approach deficiencies spotted by Captain Webb and others had been built right into the new U. S. Navy airplane.
In the end, the Hawk’s single-speed brake under the fuselage, where it cannot be used in landings, was replaced on the T-45A by a pair of fuselage side brakes. These are just ahead of and under the horizontal tail (Figure 12.5). Carrier landings are made with speed brakes extended and at a high thrust level to overcome speed brake drag. At the higher thrust levels, modulation is rapid and effective in controlling the flight path. Also, just to be sure that student pilots stay out of path control trouble, the T-45A’s flight idle RPM was increased from 55 to 78 percent of maximum, by adding an approach idle stop to the throttle mechanism.
There were other changes made to the T-45A, relative to the Hawk, based on Navy flight tests. This all took place after full-scale engineering development had been started back in 1984. Hydraulically operated wing slats were added to increase wing maximum lift coefficient, a higher-thrust Rolls Royce Adour engine was installed to increase forward acceleration and reduce altitude loss when a waveoff was required, the vertical tail span
|
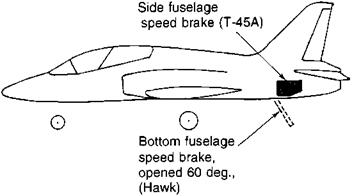
Figure 12.5 Path control problems for carrier landings required changes to the McDonnell-Douglas T-45A Goshawk. Speed brakes were moved from the bottom to the side of the fuselage. (From Jane’s AH the World’s Aircraft)
|
was increased, and a yaw damper and rudder-to-aileron interconnect was added to improve lateral-directional (Dutch roll) behavior. Captain Webb had complained about this following his Hawk flights in 1983.
Also, bearing specifically on the thrust lag problem during carrier-landing operations, the Navy installed modified Lucas fuel controls on the T-45A’s Adour engines, to minimize thrust lag when power increases are called for. Finally, the speed brakes are interconnected to the horizontal stabilizer to minimize trim changes when the brakes are extended or retracted.