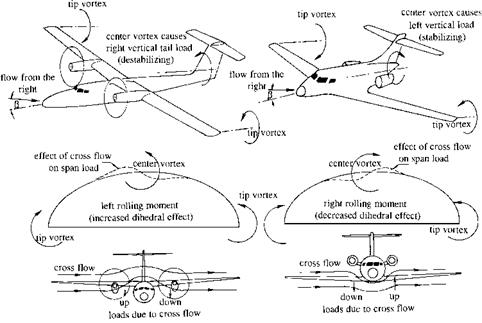
While proper stability and control design, supplemented by artificial means such as control centering devices and wing levelers, are fundamental to safe airplanes, some
|
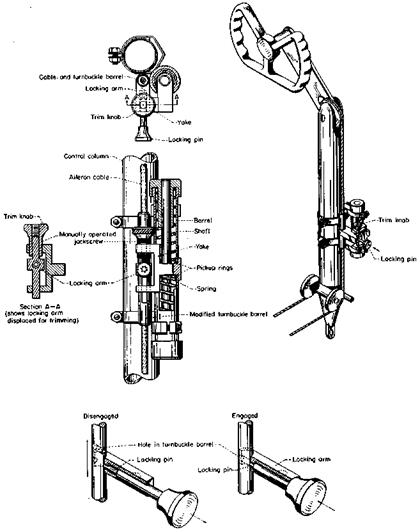
Figure 15.5 Aileron-centering device tested on a Cessna 190. The cylindrical barrel encloses two preloaded compression springs, overcoming control system friction to provide aileron centering. Trim and device engagement are both done manually by the pilot. (From Campbell, Hunter, Hewes, and Whitten, NACA Rept. 1092, 1952)
|
safety deficiencies can apparently be made up with the right kind of cockpit displays or instruments (Loschke, Barber, Enevoldson, and McMurty, 1974). They reported that on a light twin-engine airplane, a flight director display is of significant benefit during ILS approaches in turbulent air.
Heavy pilot workload during such approaches had been found in an earlier survey of general-aviation airplanes, making precise instrument tracking difficult even for experienced instrument pilots. However, the flight director instrument, which combines inputs from attitude and rate gyros and in effect tells the pilot how to move the controls, reduces somewhat this excessive workload. Even greater improvements in tracking during ILS approaches in turbulence are found when the flight director display is combined with an attitude-command autopilot.
|
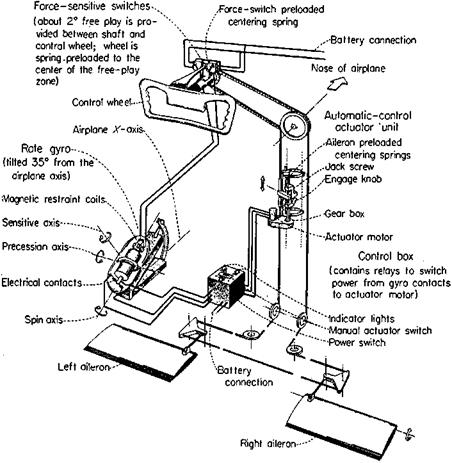
Figure 15.6 A wing-leveler device that works by moving aileron-centering springs at a low fixed rate in response to the measured rate of yaw. Wheel force switches improve maneuvers by precessing the gyro. The device was flown on a Cessna 190. (From Phillips, Kuehnel, and Whitten, NACA Rept. 1304, 1957).
|
The experiences of an airline pilot in operating heavily automated passenger-jet airplanes is relevant to the improvements provided by flight directors and automatic pilots for general – aviation airplanes. The question is how to use these devices to enhance safety for the average pilot under all operating conditions. William M. Ferree of Mount Vernon, New Hampshire, writes as follows (1994):
I’ve been a professional pilot for over 20 years and currently fly the Boeing 757 and 767. A high level of automation gives these excellent airplanes capabilities that would have been remarkable a few years ago. However, the design breaks down when some significant change of plan is introduced, which may happen because of an equipment failure or, more commonly, because of difficulty with the air traffic control system or the weather. The problem is that unless the computer is reprogrammed in these situations, it is useless. And reprogramming must often be done while landing preparation is being completed, which is an extremely busy time.
Ferree goes on to note that the 757 and 767 autopilot/flight director control panel consists of a few knobs for selecting things such as airspeed and altitude and many identical square push buttons. The panel cannot be operated by feel. The pilot must look at it in order to operate it. The argument for readily reprogrammed equipment in commercial-transport airplanes must be even more valid for general-aviation flight directors and automatic pilots.
Today’s heavily automated passenger jet airplanes have multifunction cathode ray or flat – screen displays of all flight and engine instruments, quadruplicated as backups for failure. Yet, a few old-style instruments are carried as additional insurance. All Boeing transports from the 707 on have small standby vacuum-driven gyro horizons, just to the side of the central instrument panel. This will give several minutes of reliable indication after a power failure, due to the inertia of the gyro’s rotor.
Another question related to automation of passenger jets is whether automation is reducing the competence needed in pilots. Wyatt Cook, an American Airlines pilot, reports that in flight training at the Dallas facility, one of the two pilots is required to be on raw data, meaning the VOR and ILS radio guidance signals. William H. Cook, Wyatt’s father, writes, “The basics [VOR and ILS] require a lot of work.”