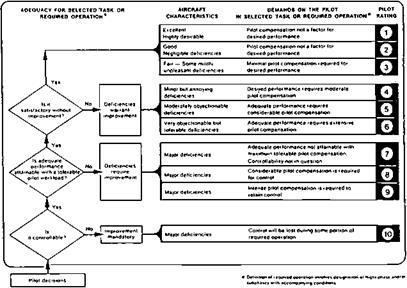
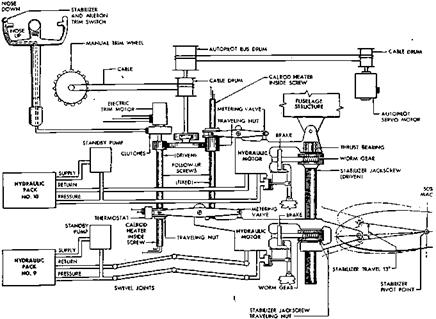
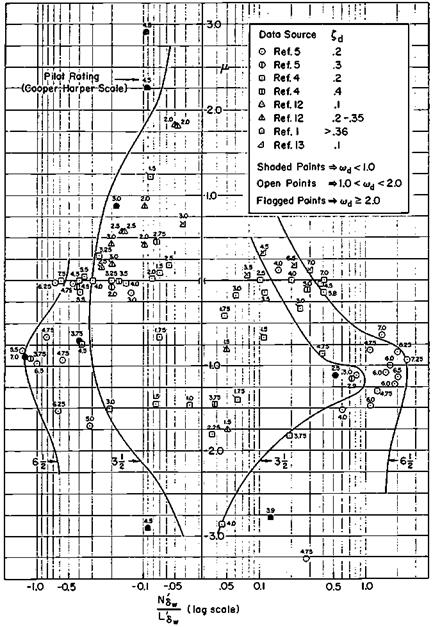
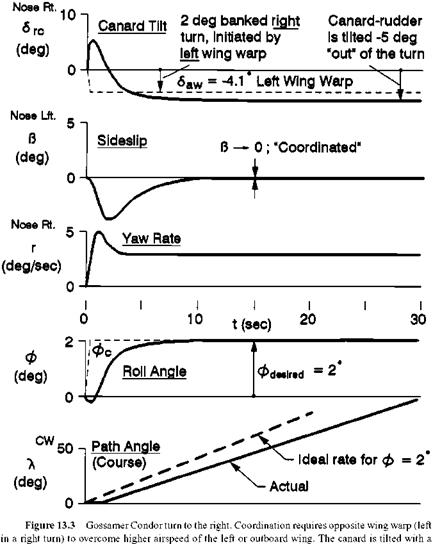
The Northrop F-89 Sideslip Stability Augmenter
The straight-wing twin-jet F-89 was originally flown with a conventional rate gyro yaw damper, with washout for steady turns. The rate gyro was replaced with a sideslip sensor, to reduce adverse (top) rudder angle in lead pursuit courses more than the yaw rate washout could do. The F-89 sideslip stability augmenter improved directional stability as well as Dutch roll damping.
20.2 Root Locus Methods of Analysis
One of the remarkable stories in the stability and control field is the invention of the root locus analysis method by Walter R. Evans. This came relatively late in the game for a fundamental advance in control system analysis. The root locus method first appeared in Evans’ Master’s degree thesis at the University of California, Los Angeles, followed by a North American Aviation report. The first root locus journal paper (Evans, 1948) was published over objections from referees who thought the work was of little
merit. While the method is known simply as the root locus method in the United States, Russian papers quite properly call it the Evans method. The root locus method received wide publicity with Dr. William Bollay’s 1950 Wright Brothers Lecture, but even before the 1948 journal publication it had “spread like wildfire,” according to Duane McRuer. This happened because John Moore at UCLA and Phillip Whittaker at MIT lectured on the method, using drafts of the North American report.
The essence of the root locus method is the set of rules that Evans discovered for the migration of roots of an open-loop system to the roots of the same system when the loop is closed. Airframe open-loop roots are nothing more than the airframe roots discussed by G. H. Bryan in 1911, the short – and long-period airplane modes of motion, and the aperiodic modes such as the spiral and roll modes. Evans found that the open-loop modes migrate toward the open-loop zeros as closed-loop gain is increased from zero (the open-loop case) to infinity. The open-loop zeros are the roots of the numerator function of each element’s transfer function.
Root locus methods survived from the 1950s to the present day as one of the most widespread flight control system analysis and synthesis methods. Modern variants are
z-Plane The z-plane root locus makes use of the z-transform, where z = eTs and s is the Laplace transform variable (Bollay, 1951). The complex number z is defined only at the switching or sampling times T of a sampled-data or digital control system. Since the states of sampled-data or digital control systems are likewise defined only at sampling times T, the z-plane root locus can be used for stability and performance analysis of these systems. In the z-plane, real parts of the variable z are plotted along the abscissa, while imaginary parts are plotted along the ordinate. The Evans s-plane root locus rules apply as well in the z-plane. Only the region of stability and lines of constant damping ratio differ.
w – and w ‘-Planes An improved transformation method for dealing with sampled-data or digital systems appeared in the 1950s, called the w-plane. The complex variable w iscreated by a bilinear transformation on z, or w = (z — 1)/(z +1). Richard F. Whitbeck and L. G. Hofmann (1978) describe a scaled version of the w-domain with even better properties. This is the w’-domain, in which w’ = 2w/T. In contrast to the z-plane, the left or stable half of the w ‘-plane corresponds to the left or stable half of the s-plane. Powerful analogies exist between the s – and w’-domains, allowing use of conventional root locus and Bode (Bollay, 1951) design tools. As a drawback, w’ transfer functions are far more complex algebraically than s transfer functions.
Unified Analysis Using Bode Root Locus The Bode root locus is a hybrid method developed by Duane McRuer (McRuer, Ashkenas, and Graham, 1973) that adds to the conventional Bode plot the amplitude ratios of the various loci in the s-plane. For any given loop gain actual closed-loop roots, all of the conventional frequency response quantities and the sensitivity to gain changes are seen in this plot.
Root Locus Sensitivity Vectors Sensitivity vectors can be drawn from unaugmented airplane poles, such as the Dutch roll complex conjugate pair, giving the directions and magnitude in the complex plane of the migration of those poles for individual feedbacks. The effects on a Dutch roll mode of unconventional feedbacks, such as sideslip and lateral acceleration to the ailerons, can be compared. Root locus sensitivity vectors were first published by Duane McRuer and Robert Stapleford (1963).