In nearly 100 years of controlled flight the stability and control field has seen any number of special gadgets and phenomena that fit into no general category We recall some of the most interesting of these.
14.1 Fuel Shift and Dynamic Fuel Slosh
The term fuel shift refers to long-term motions of the fuel in a partially filled tank, such as a shift to the rear of an airplane’s tank caused by a prolonged nose-up attitude, in a climb. The causes and effects of fuel shift are apparent. Aft fuel shift could move the airplane’s center of gravity to a dangerously rearward position. This possibility is generally considered by every designer. There is even the possibility of fuel starvation if the tank feeds the airplane’s engine from a forward sump.
Dynamic fuel slosh occurs when fuel in a partially filled tank, be it an automobile or airplane tank, sloshes around inside the tank in response to changing vehicle accelerations. As the tank walls contain the sloshing fuel, transient forces are transmitted to the walls, and the vehicle, by the fuel. Dynamic fuel slosh can be a problem in airplane stability and control if the fuel modes of motion couple with the airplane’s normal modes of motion. The dynamic fuel slosh problem is worth examining because modern jet airplanes tend to have high ratios of fuel to gross weight and slosh motions could have a considerable effect. Also, on airplanes with relatively thin wings, the main tankage tends to be in the fuselage. Wing tanks are generally interrupted by structural members, which act as baffles to fuel motion, while fuselage tanks can have large uninterrupted volumes.
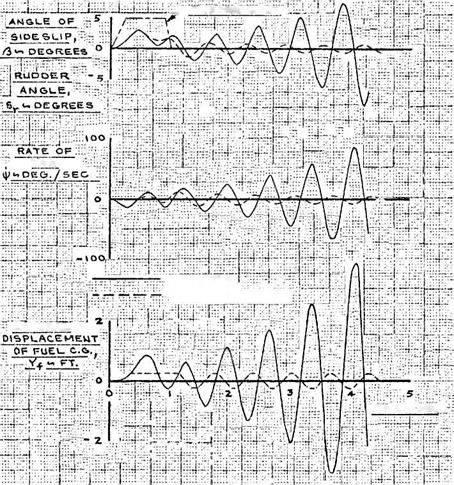
Although dynamic fuel slosh is an intriguing mathematical and engineering problem, documented cases of dynamic fuel slosh coupling with an airplane’s modes of motion are rare. There was a verified case of dynamic fuel slosh coupling with the Dutch roll mode of motion on the Douglas A4D Skyhawk. Partial fuel in a 500-gallon fuselage tank forward of the center of gravity caused undamped roll-yaw oscillations during landing approaches (Figure 14.1). The problem was corrected when fore-and-aft vertical tank baffles were added to the fuselage tank, dividing the tanks into left and right halves. The baffles almost doubled the fuel slosh frequency, decoupling slosh from the Dutch roll.
There was another reported dynamic fuel slosh problem on the Lockheed F-80C airplane. This was during an all-out drive to improve the loitering capability of F-80s in the early months of the Korean War. F-80 units in Korea started carrying unbaffled 265-gallon tip tanks, but soon reported unexplained crashes. At the request of Headquarters, Far East Air Forces, Wright Field flight-tested the 265-gallon tanks on an F-80C.
In a test flight in November 1950, James D. Kelly found no flight problems at takeoff and climb-out, when the wing tip tanks were essentially full. Later, with partial tip tank fuel, an uncontrollable pitching motion started. Kelly could see the wing tips twisting as fuel sloshed fore and aft. He recovered control only after the left tip tank collapsed and fell away and he could jettison the right tank.
 —1^—R UPPER mPUT
—1^—R UPPER mPUT
VAW
LIMUMITEO ; i;:
f • • ‘ .1 • ‘ *: Y^. LIMITED TO. IS FT.
Later лі
ті me hSEC
Figure 14.1 Calculated effectof fuselage tank slosh in the Douglas A-4 Skyhawk before installation of a fuselage tank baffle. Fuel motion couples with the Dutch roll mode of motion. With the fuel mass motion limited by the tank sides (dotted curves), a steady limit cycle “snaking” motion results. (From Abzug, Douglas Rept. ES 29551, 1959)
Two additional dynamic fuel slosh cases are known, both documented in U. S. Air Force flight test reports. Both involved fuel slosh coupling with the Dutch roll mode of motion and were excited when the rudder was used to stop the yawing component of the Dutch roll motion. The airplanes with this problem were the Boeing KC-135A and the Cessna T-37A.
An analytical approach to the problem of dynamic fuel slosh coupling with the modes of airplane motion was made possible by a model proposed by Ernest W. Graham (Luskin and Lapin, 1952). Graham used the velocity potential for liquid in a rectangular open-top tank given in Horace Lamb’s classic Hydrodynamics. Sloshing fuel is modeled as a simple pendulum plus a fixed mass below the pendulum. The pendulum angle from the vertical is taken as the average fuel surface angular displacement in its fundamental mode of motion (Figure 14.2). The fuel’s general motion has higher harmonics, of shorter wave lengths, all of which are neglected to define the equivalent pendulum.
|
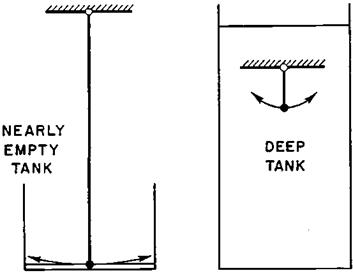
Figure 14.2 Ernest W. Graham’s pendulum analogy to sloshing fuel in open-top rectangular tanks, illustrated by two extreme cases. All of the fuel sloshes in the nearly empty tank, but in just the upper portion of the deep tank. (From Luskin and Lapin, Jour. of the Aeronautical Sciences, 1952)
|
The pendulum analogy to dynamic fuel slosh depends mainly on the depth of the fuel in the tank. In the nearly empty case, fuel slosh is simply the wave action in a shallow container. The equivalent pendulum is long, and so is the period of the sloshing motion. In the nearly full or deep tank, the equivalent pendulum is short and so is the slosh period. Graham’s model permitted subsequent analysts to treat the problem of fuel slosh by adding the equivalent pendulum to the equations of airplane motion, as an additional degree of freedom for each partially filled tank.
Albert A. Schy, a skilled NACA analyst, set up the fuel slosh problem without using the Graham pendulum model, by assuming fuel is carried in spherical tanks (Schy, 1952). While spherical tanks are never seen in airplanes, Schy’s model is altogether equivalent to Graham’s model for conventional rectangular or prismatic tanks. Schy’s calculations show significant coupling into the Dutch roll mode of an airplane when the sloshing fuel mass is one-fourth the weight of the airplane.
Dynamic fuel slosh coupling with the longitudinal short – and long-period modes of motion is seldom a problem. There is a slight loss in short-period mode damping, but the long-period or phugoid mode cannot couple measurably with fuel in a partially filled tank unless the fore and aft dimension of the tank is impossibly long (Luskin and Lapin, 1952). Recent dynamic fuel slosh studies on a modern swept-wing jet with long fuel tanks running parallel to the wing spars came up dry, in the sense that slosh in any pair of partially filled tanks had negligible effects on the aircraft’s modes of motion.
In contrast to the modest effects of dynamic fuel slosh (but not long-term fuel shift) for the airplane case, dynamic fuel slosh has been an ongoing concern for large liquid-fueled boost or launch vehicles, such as NASA’s Saturn V Launch vehicle dynamic fuel slosh problems have included coupling with controlled pitch and yaw modes of motion as well as with elastic body bending modes.
Turning to the fuel shift problem in airplanes, an interesting case occurred on the Douglas A4D Skyhawk during early test flights. The A4D’s ultrasimple fuel system has only two
|
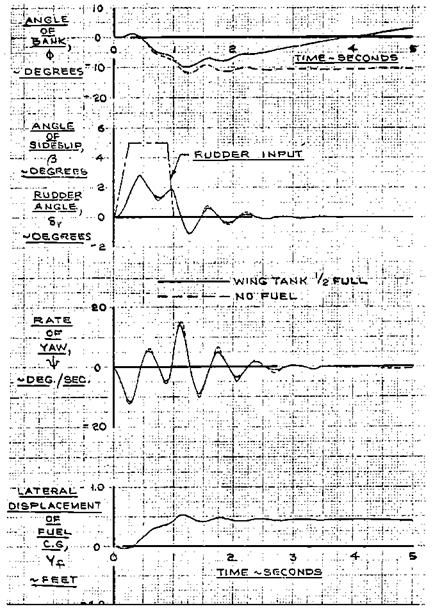
Figure 14.3 Calculated effect of fuel shift in the Douglas A-4 Skyhawk’s wing tip—to—wing tip wing tank. With half-wing fuel, a rudder kick shifts the fuel, giving apparent spiral instability. The bank angle increases slowly with time. (From Abzug, Douglas Rept. ES 29551, 1959)
|
tanks, the fuselage tank, which had sloshing problems before a baffle was installed, and a single integral wing fuel tank, which runs from wing tip to wing tip. The wing ribs provide excellent slosh baffling, but prolonged lateral acceleration can transfer partial wing fuel across the airplane’s centerline.
A4D wing fuel shift shows up as spiral instability, easily corrected by the ailerons (Figure 14.3). However, the early A4D airplanes had a single, or nonredundant, aileron hydraulic
system. When aileron hydraulics malfunctioned at a high Mach number during an early test flight the airplane and pilot James Verdin were lost. The painful lesson was learned. Production A4D (now A-4) airplanes retain the single integral wing fuel tank, but dual, independent aileron power systems now guard against loss in lateral control due to fuel shift.
Another fuel shift incident from the same time period occurred at Wright Field in a North American YF-100 being flown by Captain H. Z. Hopkins. He took off for a short functional check of the 275-gallon external fuel tanks. Only 50 gallons were loaded into each tank; takeoff acceleration shifted this load aft. Fuel was being burned from the forward fuselage tank, adding to the aft shift in cg. The cg apparently shifted aft behind the maneuver point, the point at which pull stick forces are required for positive-load factors. The airplane went through a rapid sequence of positive and negative maneuvers. The external tank fuel somehow shifted forward, and the structurally damaged airplane was brought back under control and landed.












 —1^—R UPPER mPUT
—1^—R UPPER mPUT