A computational study of the flow past the HOPPER/PHOENIX configuration dealt in particular with thermal surface effects [4]. The RV-W HOPPER was a sub-orbital rocket-propelled single stage space-transportation system studied in the frame of FESTIP, see, e. g., [1].
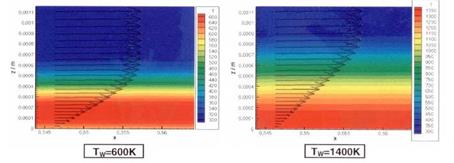
We consider a result found for a re-entry trajectory point with the speed vж « 1 km/s at H « 37 km altitude. The flow parameters are given in Table 10.5. The skin friction was obtained with fully turbulent RANS solutions for two wall-temperature conditions: a) Tw « 500 K, which in the surface part shown in Fig. 10.4 approximately is the radiation-adiabatic temperature belonging to the trajectory point, b) Tw « 1,600 K, which in the shown surface part approximately is the radiation-adiabatic wall temperature belonging to Мж = 14.4 and vж « 4.7 km/s at H « 55 km altitude.
Condition b) with the higher wall temperature resembles the thermal reversal situation of the Space Shuttle Orbiter mentioned in Section 3.1. It is, however, a generic condition.
|
Table 10.5. Parameters of the flow past the HOPPER/PHOENIX configuration
[4].
|
Moo
|
R&L, oo
|
L [m]
|
Too [K]
|
а П
|
Villlf l ]
|
T„ [K]
|
Boundary-layer state
|
|
3.2
|
8.071-106
|
50.2
|
242.22
|
15
|
20
|
~500/~l,600
|
turbulent
|
|
Fig. 10.4 shows for condition a) a skin-friction coefficient from the left to the right between cf « 0.005 and 0.0025, and for condition b) between cf « 0.003 and 0.0015. That means that we have a distinctly smaller skin friction for the higher wall temperature.
The effect that the higher wall temperature leads to a smaller (turbulent) skin friction is clearly seen. But there are at least two major side effects and a minor one:
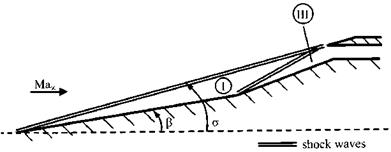
— First to the in Fig. 10.4 at once noticeable major side effect. For condition a) around the hinge line a small separation zone is present, which indicates a—slightly three-dimensional—Edney type VI interaction, typically present at such a supersonic compression ramp, Sub-Section 9.2.1. Downstream of it on the flap the asymptotic ramp flow, although threedimensional, is present: the—not shown—surface pressure coefficient attains the asymptotic behavior, which characteristically is a plateau [1].
For the higher wall temperature, condition b), we see a considerably enlarged—and more three-dimensional—interaction zone with reduced skin
|
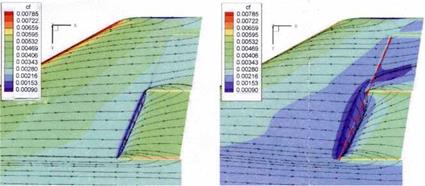
Fig. 10.4. Flow past the lower left wing side of the HOPPER/PHOENIX configuration [4]. Influence of the wall temperature on the skin friction. Left part, condition
a) : radiation-adiabatic wall temperature Tw & 500 K (є = 0.8), right part, condition
b) : Tw & 1,600 K. Inboard wing flap deflection niwf = +20° (downward). The flow is from the left to the right. The view is towards the lower (windward) side.
|
friction on the flap, and—not shown—a markedly reduced surface pressure.[175] This reflects the influence of the wall temperature on the tangential boundary-layer profile discussed in Section 10.2. The wall-near momentum flux in the boundary layer is reduced and the flow reacts stronger on an adverse pressure gradient.
The outcome of this side effect is that with the hotter wall the efficiency of the flap is reduced. Generally we note that this holds for any aerodynamic trim or control surface. A detrimental effect would also be present on inlet ramps.
— The second major side effect becomes obvious, if we recall that a hotter surface increases the boundary-layer thickness, the displacement thickness etc., Section 10.2. A larger boundary-layer thickness means—besides an intensified shock/boundary-layer interaction—an increase of the pressure or form drag of a body (wing, fuselage, etc.), an increase of the decambering of an airfoil, etc. [3]. A reduction of the skin-friction drag can be nullified, at least partly, by one or more of these effects.
— The patterns of the skin-friction show that the three-dimensionality of the attached viscous flow ahead of the flap is slightly enlarged for the higher wall temperature, as is to be expected [3]. This minor side effect may lead— at least in the boundary-layer part of the flow—to a deviation from the ideal onset flow of the flap: two-dimensional and normal to the hinge line.
Whether one or all of these effects are important for a flight vehicle, in particular for a CAV, depends on its shape, its mission, the part of the trajectory, and so on. Regarding the form drag, for instance, one should note that trailing edges of hypersonic vehicles may have a considerable thickness in order to cope with the thermal loads.
Generally the question of turbulence modeling for flows with embedded strong interaction phenomena must be considered, Sub-Section 9.2.1 and Section 8.5. Basically, however, the above results can be trusted. The problems usually are those with the prediction of the thermal loads in the interaction zone.