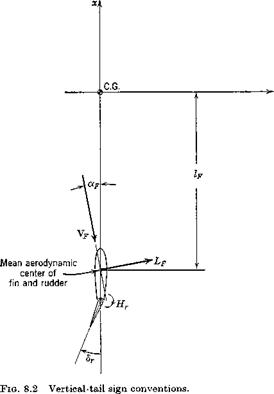
THE DERIVATIVE C
By contrast with C, the derivative G^, known as the dihedral effect, is of paramount importance. We have already noted its relation to roll stiffness and to the tendency of airplanes to fly with wings level. The primary contribution to Ct is from the wing—its dihedral angle, aspect ratio, and sweep all being important parameters.
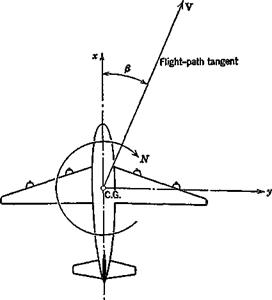
The effect of wing dihedral is illustrated in Fig. 8.7. With the coordinate system shown, the normal velocity component Vn on the right wing panel (R) is, for small dihedral angle Г,
Vn = w cos Г + v sin Г = w + г>Г
and that on the other panel is w — «Г. The terms ±vT/V = ±/?Г represent opposite changes in the angle of attack of the two panels resulting from sideslip. The “upwind” panel has its angle of attack and therefore its lift increased, and vice versa. The result is a rolling moment approximately Unear in both /? and Г, and hence a fixed value of 0^ for a given Г. This part of Gt is essentially independent of wing angle of attack so long as the flow remains attached.

Vn = normal velocity of panel R — w cos Г + v sin Г = ад + vP
vV VBT n
/. Aa of R due to dihedral === •*—■ = ——— = /5Г
|
|
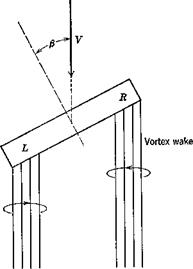
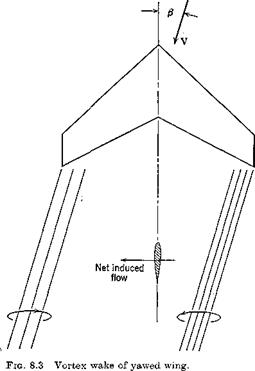
Even in the absence of dihedral, a flat lifting wing panel has a Ct proportional to CL. Consider the case of Fig. 8.8. The vertical induced velocity (downwash) of the vortex wake is greater at L than at R simply by virtue of the geometry of the wake. Hence the local wing angle of attack and lift are less at L than at R, and a negative Gt results. Since this effect depends, essentially linearly, on the strength of the vortex wake, which is itself proportional to the wing CL, then the result is ДGt^ oc CL.