GENERAL THEORY OF STATIC LONGITUDINAL STABILITY
The concept of static stability was introduced in Chapter 3, where it was identified with the nature of the exponential characteristic modes (Figs. 3.6a and b). In Sec. 3.3 (p. 70) it was pointed out that the vanishing of the constant term in the characteristic equation of a linear/invariant system provides a boundary between asymptotic stability and static instability. This is the criterion that we discuss in this section, and relate to the stability criteria presented earlier in Chapter 6.
The characteristic equation [see (3.3,7)] is
|sl – A| = 0
and clearly the constant term is found by setting s = 0, i. e.
co = I —A|
The criterion for static stability is then
![]() I—A| > 0
I—A| > 0
The application of this criterion is in principle straightforward for any of the linear/invariant systems (5.13,18 to 20) that describe the longitudinal and lateral motions. In the interests of deriving a simple usable analytical result, however, we shall treat the special case represented by (9.1,1), in which the equilibrium flight path is horizontal, and z derivatives are neglected. When I —A| is expanded we get
Since the factor outside the square brackets is always positive (CL. could not be <—2fi for any reasonable heavier-than-air vehicle) the stability criterion becomes
![]() (9.3,3)
(9.3,3)
When comparing (9.3,3) with the static stability criteria discussed in Chapter 6, a minor difference in basic assumptions must be noted. In the preceding development, it was specifically assumed that the thrust vector rotates wdth the vehicle when a is changed. In the development leading to (6.4,24) by contrast, there is an implicit assumption that the thrust provides no component of force perpendicular to V [see (6.4,18)]. It is this difference that leads to the presence of CD in (9.3,3) whereas there is no corresponding term in the numerator of (6.4,24). Had the assumptions been the same, the expressions would be strictly compatible. In any case, °De is usually small compared to CL so that the difference is not important. We see that the justification for the statement made in Sec. 6.4, that the slope of the elevator trim curve (ddetrimldf)^ is a criterion of static stability, is provided by (9.3,3). [Note that CWf = CLe in (9.3,3).]
Another stability criterion referred to in Chapter 6 is the derivative dCmjdCL (6.3,21). It was pointed out there that this derivative can only be said to exist if enough constraints are imposed on the independent variables a, f, de, q, etc., on which Gm and CL separately depend. Such a situation results if we postulate that the vehicle is in rectilinear motion (q = 0) at constant elevator angle and throttle setting, with L = W, but wdth varying speed and angle of attack. Such a condition cannot, of course, actually occur in flight because the pitching moment could be zero at only one speed, but it can readily be simulated in a wind tunnel where the model is restrained by a balance. [The argument that follows is quite similar to that of (6.4,18) et seq.] With the above stipulations, Gm and CL reduce to functions of the
two variables V and a, and incremental changes from a reference state ( are given by
![]() dCL = Cr da + 0LdV
dCL = Cr da + 0LdV
dOm — da + Cmy dV
The required derivative is then
provided dV/da exists. This is guaranteed by the remaining condition imposed, i. e. L — W (implying aT = 0). For then we have
W = 0L(a, t)ipV2S = const
from which we readily derive
(CLx da + CLy dV)yV*S + CLePVeS dV = 0 (9.3,6)
From (9.3,6)
{CLv + 2CLJ dV + CLa da = 0
After substituting (9.3,7) into (9.3,5) and simplifying we get
On comparing (9.3,8) with (9.3,3), again neglecting 0D thereinfor compatibility of assumptions, and noting that Gw = ОL, we see that the static stability criterion is
dP
![]() <0 (9.3,9)
<0 (9.3,9)
L=W provided that dCmldCL is calculated with the constraints A(Se = Дтг = q = 0 and L = W. [The quantity on the left side of (9.3,8) and (9.3,9) is sometimes referred to as speed stability in the USA, by contrast with “angle of attack” stability. In Great Britain, this term usually has a different meaning, as in Sec. 11.5.]
On using the definition of hs given in (6.4,26) we find from (9.3,8) that
i. e. that it is proportional to the “stability margin,” and when CLT < 2GLe’ is equal to it.
Finally, we must check on the significance of the “pitch stiffness” parameter Gmx, to which great importance was attached in Chapter 6. We see from
9.3,3 that when 0Ly and Cmy are zero, Cm < 0 does indeed provide an exact criterion for static stability. Even when CLy and Gm are not zero, we shall see from the examples to follow that Cma < 0 is still a useful and significant criterion.











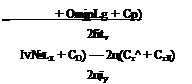
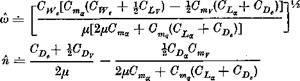
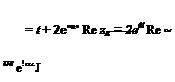
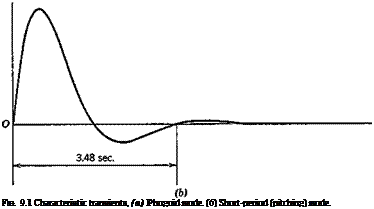
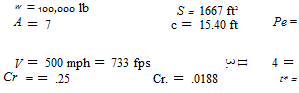 60 psf
60 psf