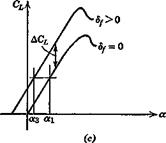
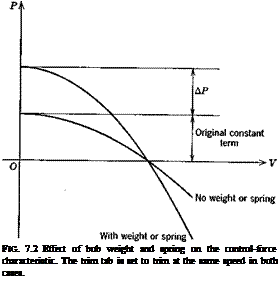
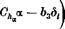THE FORWARD LIMIT
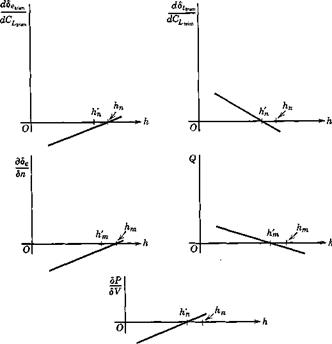
As the C. G. moves forward, the stability of the airplane increases, and larger control movements and forces are required to maneuver or change the trim. The forward C. G. limit is therefore based on control considerations and may be determined by any one of the following requirements:
(i) The stick force per g shall not exceed a specified value.
(ii) The stick-force gradient at trim, dPfdV, shall not exceed a specified value.
(iii) The stick force required to land, from trim at the approach speed, shall not exceed a specified value.
(iv) The elevator angle required to land shall not exceed maximum up elevator.
(v) The elevator angle required to raise the nose-wheel off the ground at take-off speed shall not exceed the maximum up elevator.
7.4 LONGITUDINAL AERODYNAMIC DERIVATIVES
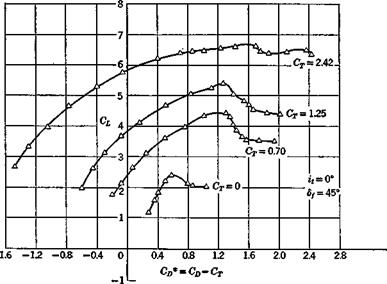
The small-disturbance equations of motion given in Chapter 5 used the technique of expressing aerodynamic forces and moments in terms of the aerodynamic derivatives. The remainder of this chapter is devoted to a discussion of these derivatives. Some of the main aerodynamic derivatives have already been discussed in some detail in Chapter 6, i. e. CL , Gm^, Ghe^, CLs, Gmg, and GheS – Of the remaining a derivatives, CD is immediately obtained from (6.1,2) as
where GLf is the value of CL in the reference equilibrium flight condition.
The thrust derivative GT^ is not readily predicted by theory, and would usually be small enough to neglect.