CHAPTER I
This book is about the motion of vehicles that fly in the atmosphere. As such it belongs to the branch of engineering science called applied mechanics. The three italicized words above warrant further discussion. To begin with fly—the dictionary definition is not very restrictive, although it implies motion through the air, the earliest application being of course to birds. However, we also say “a stone flies” or “an arrow flies,” so the notion of sustention (lift) is not necessarily implied. Even the atmospheric medium is lost in “the flight of angels.” We propose as a logical scientific definition that flying be defined as motion through a fluid medium or empty space. Thus a satellite “flies” through space and a submarine “flies” through the water. Note that a dirigible in the air and a submarine in the water are the same from a mechanical standpoint—the weight in each instance is balanced by buoyancy. They are simply separated by three orders of magnitude in density. By vehicle is meant any flying object that is made up of an arbitrary system of deformable bodies that are somehow joined together. To illustrate with some examples: (1) A rifle bullet is the simplest kind, which can be thought of as a single ideally-rigid body. (2) A jet transport is a more complicated vehicle, comprising a main elastic body (the airframe and all the parts attached to it), rotating subsystems (the jet engines), articulated subsystems (the aerodynamic controls) and fluid subsystems (fuel in tanks). (3) An astronaut attached to his orbiting spacecraft by a long flexible cable is a further complex example of the general kind of system we are concerned
with. Note that by the above definition a vehicle does not necessarily have to carry goods or passengers, although it usually does. The logic of the definitions is simply that the underlying engineering science is common to all these examples, and the methods of formulating and solving problems concerning the motion are fundamentally the same.
As is usual with definitions, we can find examples that don’t fit very well. There are special cases of motion at an interface which we may or may not include in flying—for example, surface ships, hydrofoil craft and air-cushion vehicles. In this connection it is worth noting that developments of hydrofoils and ACV’s are frequently associated with the Aerospace industry. The main difference between these cases, and those of “true” flight, is that the latter is essentially three-dimensional, whereas the interface vehicles mentioned (as well as cars, trains, etc.) move approximately in a two-dimensional field. The underlying principles and methods are still the same however, with certain modifications in detail being needed to treat these “surface” vehicles.
Now having defined vehicles and flying, we go on to look more carefully at what we mean by motion. It is convenient to subdivide it into several parts:
Gross Motion:
(i) Trajectory of the vehicle mass center.
(ii) “Attitude” motion, or rotations of the vehicle “as a whole.”
Fine Motion:
(i) Relative motion of rotating or articulated sub-systems, such as engines, gyroscopes, or aerodynamic control surfaces.
(ii) Distortional motion of deformable structures, such as wing bending and twisting.
(iii) Liquid sloshing.
This subdivision is helpful both from the standpoint of the technical problems associated with the different motions, and of the formulation of their analysis. It is surely self-evident that studies of these motions must be central to the design and operation of aircraft, spacecraft, rockets, missiles, etc. To be able to formulate and solve the relevant problems, we must draw on several basic disciplines from engineering science. The relationships are shown on Fig. 1.1. It is quite evident from this figure that the practicing flight dynamicist requires intensive training in several branches of engineering science, and a broad outlook insofar as the practical ramifications of his work are concerned.
In the classes of vehicles, in the types of motions, and in the medium of flight, this book treats a restricted set of all possible cases. Its emphasis is on the flight of airplanes in the atmosphere. The general equations derived,
|
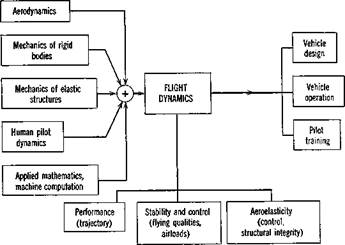
Fig. 1.1 Block diagram of disciplines.
|
and the methods of solution presented, are however readily modified and extended to treat the other situations that are embraced by the general problem.
All the fundamental science and mathematics needed to develop this subject existed in the literature by the time the Wright brothers flew. Newton, and other giants of the 18th and 19th centuries, such as Bernoulli, Euler, Lagrange, and Laplace, provided the building blocks in solid mechanics, fluid mechanics, and mathematics. The needed applications to aeronautics were made mostly after 1900 by workers in many countries, of whom special reference should be made to the Wright brothers, G. H. Bryan, F. W. Lanchester, J. C. Hunsaker, H. B. Glauert, В. M. Jones, and S. B. Gates. These pioneers introduced and extended the basis for analysis and experiment that underlies all modern practice. f This body of knowledge is well documented in several texts of that period, e. g. ref. 1.4. Concurrently, principally in the USA and Britain, a large body of aerodynamic data was accumulated, serving as a basis for practical design.
Newton’s laws of motion provide the connection between environmental forces and resulting motion for all but relativistic and quantum-dynamical processes, including all of “ordinary” and much of celestial mechanics. What then distinguishes flight dynamics from other branches of applied mechanics?
f An excellent account of the early history is given in the 1970 von Karman Lecture by C. D. Perkins (ref. 1.13).
Primarily it is the special nature of the force fields with which we have to be concerned, the absence of the kinematical constraints central to machines and mechanisms, and the nature of the control systems used in flight. The external force fields may be identified as follows:
“Strong” fields:
(i) Gravity
(ii) Aerodynamic
(iii) Buoyancy
“Weak” fields:
(iv) Magnetic
(v) Solar radiation
We should observe that two of these fields, aerodynamic and solar radiation, produce important heat transfer to the vehicle in addition to momentum transfer (force). Sometimes we cannot separate the thermal and mechanical problems (ref. 1.5). Of these fields only the strong ones are of interest for atmospheric and oceanic flight, the weak fields being important only in space. It should be remarked that even in atmospheric flight the gravity force can not always be approximated as a constant vector in an inertial frame. Rotations associated with Earth curvature, and the inverse square law, become important in certain cases of high-speed and high-altitude flight (Chapters 5 and 9).
The prediction and measurement of aerodynamic forces is the principal distinguishing feature of flight dynamics. The size of this task is illustrated by Eig. 1.2, which shows the enormous range of variables that need to be considered in connection with wings alone. To be added, of course, are the complications of propulsion systems (propellers, jets, rockets) and of compound geometries (wing + body + tail). ‘
As remarked above, Newton’s laws state the connection between force and motion. The commonest problem consists of finding the motion when the laws for the forces are given (all the numerical examples given in this book are of this kind). However we must be aware of certain important variations:
1. Inverse problems of first kind—the system and the motion are given and the forces have to be calculated.
2. Inverse problem of the second kind—the forces and the motion are given and the system constants have to be found.
3. Mixed problems—the unknowns are a mixture of variables from the force, system, and motion.
Examples of these inverse and mixed problems often turn up in research, when one is trying to deduce aerodynamic forces from the observed motion
of a vehicle in flight or of a model in a wind tunnel. Another example is the deduction of harmonics of the Earth’s gravity field from observed perturbations of satelhte orbits. These problems are closely related to the “plant identification” or “parameter identification” problem that is of great current interest in system theory. (Inverse problems were treated in Chapter 11 of Dynamics of Flight—Stability and Control, but are omitted here.)
TYPES OF PROBLEMS
The main types of flight dynamics problem that occur in engineering practice are:
1. Calculation of “performance” quantities, such as speed, height, range, and fuel consumption.
2. Calculation of trajectories, such as launch, reentry, orbital and landing.
3. Stability of motion.
4. Response of vehicle to control actuation and to propulsive changes.
5. Response to atmospheric turbulence, and how to control it.
6. Aeroelastic oscillations (flutter).
7. Assessment of human-pilot/machine combination (handling qualities).
It takes little imagination to appreciate that, in view of the many vehicle types that have to be dealt with, a number of subspecialties exist within the ranks of flight dynamicists, related to some extent to the above problem categories. In the context of the modern aerospace industry these problems are seldom simple or routine. On the contrary they present great challenges in analysis, computation, and experiment.
This book originally was intended to be a modest revision of my earlier work, Dynamics of Flight—Stability and Control, published in 1959. As the task progressed, however, I found that the developments of the intervening decade, and the shift in my own approach to the subject, made a “modest revision” impossible. Thus this volume is virtually a new book, with organization and content substantially different from its predecessor. Two principal factors caused this change: (1) the proliferation of vehicle types and flight regimes, particularly hypersonic and space flight, and (2) the explosive growth of machine computation.
The first factor compelled me to abandon the long-standing simplifying assumption that the Barth’s surface could be represented by a plane fixed in inertial space, and to include in the mathematical model all the complications that arise from the curvature and rotation of the Earth.
The second factor had two profound effects. One was that since we are no longer confined to primitive computation methods, it is commonplace nowadays in industry to construct highly sophisticated mathematical “simulations” of systems for the purpose of carrying out research and design studies. The emphasis on simple approximations is thereby reduced, and the need to set up accurate (even though complicated) mathematical models increased. The other effect of the computing revolution (on me at any rate) has been to produce a shift to modern algebra (vcetor/matrix analysis) as the basic tool for analysis. This is ideally suited to digital computation. A
tertiary effect has derived from the ready availability to me of sophisticated computing machinery, which I have used for the computation of many numerical examples, to illustrate both typical results and how to apply the theory.
I have continued as in the previous hook, to emphasize fundamentals since, as I stated in the preface to Dynamics of Flight—Stability and Control, “The art of airplane and missile design is progressing so rapidly, and the configurations and flight regimes of interest are so varied that one is scarcely justified in speaking of typical configurations and typical results. Each new departure brings with it its own special problems. Engineers in this field must always be alert to discover these, and be adequately prepared to tackle them—they must be ready to discard long-accepted methods and assumptions, and to venture in new directions with confidence. The proper background for such ventures [and for such confidence] is a thorough understanding of the underlying principles and the essential techniques.” To which T. Hacker (ref. 1.11) appropriately adds that some doubt should leaven the confidence and that “the effort for a thorough understanding of principles and techniques should be completed by the desire to further. . . the former and improve the latter.”
Chapters 2 and 3 review the foundation in mathematics and system theory for the material that follows. Readers who are familiar with this material will find it useful for review and reference. For readers whose background has not included these topics, a study of these two chapters is essential to understanding the rest of the book. Chapters 4 and 5 continue with the building of a general mathematical model for flight vehicles and contain many explicit variations of such models. The aerodynamic side of the subject is explored next in Chapters 6 to 8, and specific applications, with many fully worked numerical illustrations, are given in Chapters 9 to 13. The example vehicles range from STOL to hypersonic. I have omitted the rather extensive appendices of data that were contained in the previous book, simply in the interests of economy. These data are now available in the USAF Handbook of Stability and Control Methods and the Data Sheets of The Royal Aeronautical Society. I also omitted, on the grounds of time and economy, a planned chapter on the dynamics of spacecraft entry into the atmosphere. However, the general equations of Chapter 5 embrace this application.
This book is written for both students and practicing engineers. Chapters 2 to 5 are not especially suited for an introductory course, but are appropriate for the more serious student who wishes to qualify as a practitioner in this field. The remaining chapters provide ample useful material for an introductory course when used in conjunction with a less rigorous development of the small-perturbation equations for the “flat-Earth” case.
I am grateful to my students, from whom I have learned so much, especially to those in my graduate course who used the manuscript as a text and who made useful suggestions. For helpful discussions, and constructive criticism, I thank P. C. Hughes, H. S. Ribner, G. F. D. Duff, and especially L. D. Reid, who wrote the first draft of Chapter 12. I received financial support from the U. S. Air Force, through AFOSR Grant No. 68-1490A, monitored by the Applied Mathematics branch.
For carrying out machine calculations I thank Terry Labrash, of the UTIAS staff, R. Lake and H. Gindl, undergraduate students and, above all, my son, David Alexander, who did the bulk of the computations in the summers while he was a high-school student.
I express my deepest gratitude to my wife, Maya, for giving up three summer vacations while I worked, and for her endless patience and constant encouragement. The encouragement and support of my daughter, Carol Elizabeth, also helped to sustain me throughout this task.
Toronto, 1971 BERNARD ЕТІШ
|
1
8
8
9
9
17
18
20
40
42
42
50
56
71
96
104
104
106
112
114
|