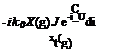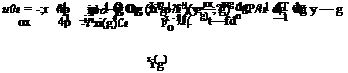When the flow speed is less than the speed of sound which means the Mach number is under unity, the flow is called subsonic. In such a flow with a free stream speed U, a disturbance which was introduced at time s becomes the spherical front, as shown in Fig. 5.2, after the time duration of At at time t.
The disturbance reaches the point r from its origin with r = a At = a(t — s)
and in terms of the coordinates x, y, z and the times given above we have
2 2 2 2 2
a (t — s) = [x — U(t — s)] + y + z. If we solve for the time of introduction of the disturbance, s, we obtain
In 5.7 we have two different times for s. For the subsonic flow we have to choose the one which has the smaller value because s — t must be negative for subsonic flows. This is possible only for the following s.
Now, we can write the velocity potential for a source generated at time s and reached the point x, y, z at time t, using Eqs. 5.5-5.6.
If the intensity of the source varies simple harmonically in time, that is q(s) = qelms, then the potential with 5.8 reads as
– f+ak _Mx-px2+b2(y2+z2 ) ] I
/(x; y; z; t) =– (5.10)
4p x2 + b2(y2 + z2)
We can also obtain 5.10 using pure mathematical approach with a Lorentz type of transformation for which time coordinate is no longer absolute and given as follows
– = x, – = by, z = bz ve – = t + Mx/ab2, b = V1 — M2 (5.11)
For this transformation, the derivatives in old coordinates in terms of the new ones read as
0 0 0- 0 0- 0 0z 0 0- 0 M 0
0x 0- 0x + 0- 0x + 0z 0x + 0- 0x 0- + ab2 0-
and
 b-, – = b-.
b-, – = b-.
b 0-, 0z b0z
The second derivatives then become:
_0l – (0 M0]2 0L- r20L 0L – r20L
0x2 0- + ab2 0t, 0y2 0-2, 0z2 0z2
In Eq. 5.14, k2 is a positive number and the derivatives, denoted by ‘prime’, of h is taken with respect to transformed time coordinate. Since the right hand side of 5.14 is constant, it gives us two separate homogeneous, coupled only with constant k, equations for the functions g and h as follows.
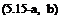
h" + a2b4k2 h = 0
V2g + k2 g = 0
Eq. 5.15-a, is simple harmonic in time. Therefore, if we take ю = ab2k the general solution of 5.15-a becomes
h (X) = heixX (5.16)
Equation 5.15-b, on the other hand, is the well known Helmholtz equation which has a solution in transformed coordinates as (Korn and Korn 1968),
e±ikR
g(X X; z)=g R-, R = Vy2 + y2 + z2 (5.17)
Combining 5.16 and 5.17, the velocity potential in terms of / = g h becomes
/(X, X, Z, X) = / eix(X±R/ab2) /R (5.18)
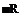
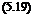
where we have two solutions separated with ±. If we go back to the original (x, y, z, t) coordinates we will have
In Eq. 5.19, for the exponential term we take the one with—sign to have solution in agreement with 5.10.
In subsonic flows the acceleration potential rather than the velocity potential is preferred for its direct relation with the lifting pressure. Therefore, let us remember the relation between the two, the acceleration and the velocity potentials, as 2.25
Utilizing Eq. 2.25 with 2.21 the acceleration potential in terms the pressure and density of the farfield we obtain
W = P1—p (5.20)
As stated before, Eq. 5.20 gives the direct relation between the acceleration potential and the surface pressure which is to be used in determining the aerodynamic coefficients. Recalling Eq. 2.26, reminds us that the acceleration potential also satisfies Eq. 2.24 whose solution for the acceleration potential is
W(x, y, z, t) = WeHt+^(Mx~R)]/R (5.21)
The acceleration potential can directly be related to the surface lifting pressure discontinuity in terms of doublet distribution. We can derive the expression for a potential written in terms of a doublet. Defining a doublet requires a pair of source and a sink which are of equal strength and distance of e apart from each other as shown in Fig. 5.3.
Now, let us express the potential for a source given by 5.21 in terms of a function f in the following manner, W = —Wf (x, y, z, t). For a sink with the same strength, the potential becomes W = Wf (x, y, z, t). The total effect of these two potentials placed on z axis with a distance e reads as

W = W[f (x, y, z — e/2, t)—f (x, y, z + e/2, t)]
If we multiply and divide 5.22 by e, and take the double limit of the resulting ratio for the strength going to infinity as e approaches zero we obtain
The limiting process employed on We results in
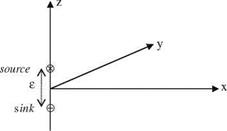 Fig. 5.3 Source and sink pair placed on z axis
Fig. 5.3 Source and sink pair placed on z axis
lim [—We] = A
jE—— 0
W—i
where A is a constant having a finite value. The limit on f is nothing but the derivative of f with respect to z, i. e.
If we take the derivative of the expression in curly parenthesis with respect to z we obtain
Now, we can comment on the physical meaning of acceleration potential given by 5.25 at the surface where z = 0. At this surface the value of potential is zero except for R = 0 where there is a singularity. Eq. 5.20 provided us the relation between the pressure and the acceleration potential. Rearranging 5.20 to obtain the pressure at a point (x, y, z) for a given time t gives us
P(X; У; z, t) =pi — PiW(X; y, z; t) (5.20)
We can express the lifting pressure in terms of the singular doublet strength A given by Eq. 5.24 as Ap = pi — pu / A. Dimensional analyses show that A must have the dimensions L4 T-2. Therefore, the strength of the doublet is related to the lifting pressure as follows
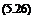 i2 Л
i2 Л
A = A p
P
Here, i is the characteristic length to be employed for defining the strength of the acceleration potential as the pressure discontinuity in following form.
We have finally obtained an expression, 5.27, for our mathematical model for lifting bodies in subsonic flows. Eq. 5.27, however, is developed for a doublet placed at the origin. In order to represent lifting surfaces, on the other hand, we need to derive the same expression for the effect of an arbitrary point on the surface.
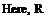 (x — n)2 + b2 (y — g)2 + Z2
(x — n)2 + b2 (y — g)2 + Z2![]() Dp(n; g; t) = DP(n, g)e“
Dp(n; g; t) = DP(n, g)e“![]() w(x, y)= ix + U0x Pa (x, y)
w(x, y)= ix + U0x Pa (x, y)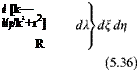












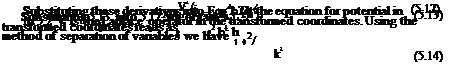
 Fig. 5.3 Source and sink pair placed on z axis
Fig. 5.3 Source and sink pair placed on z axis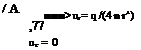
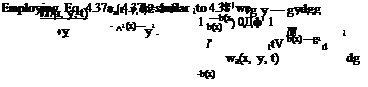
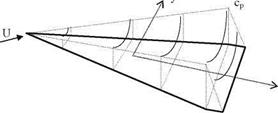
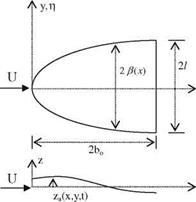 Fig. 4.6 Low aspect ratio wing
Fig. 4.6 Low aspect ratio wing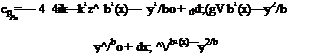

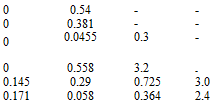
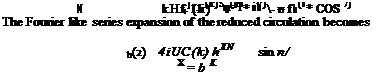
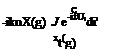 xt (g)
xt (g)