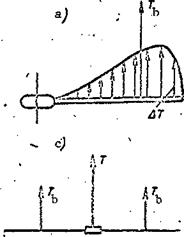
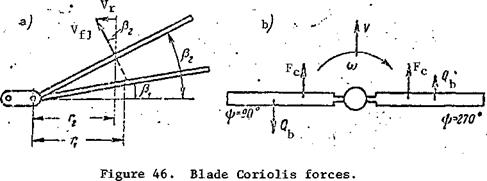
The reactive torque retards rotation of the main rotor and causes the helicopter to turn in the direction opposite that of the rotor. The turning action of the reactive torque is counteracted in various ways. On singlerotor helicopters the reactive torque is balanced by the tail rotor thrust moment (Figure 20).
Since the helicopter turns about its center of gravity, the tail rotor thrust moment is defined relative to the vertical axis of the helicopter.
The helicopter will not turn about the vertical axis if the reactive torque equals the tail rotor thrust moment, which is defined by the formula where Ъ is the distance from the helicopter center of gravity to the tail rotor.
From the formula N = M w we can determine the magnitude of the main req p b
rotor reactive torque and the equal tail rotor thrust moment
|
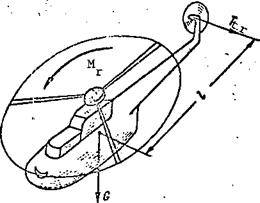
Figure 20. Balancing of main rotor reactive moment on a single-rotor helicopter.
|
|
Knowing the distance Ъ, we find the tail rotor thrust
M

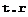 t. r.
t. r.
I ‘
Now it is not difficult to explain the purpose of the helicopter tail rotor. The tail rotor of the single-rotor helicopter is intended to create a thrust whose moment balances the main rctcr reactive torque and thereby prevents rotation of the helicopter around the vertical axis. Directional control of the helicopter is accomplished by varying the tail rotor thrust and its moment about the helicopter vertical axis.
In helicopters with two main rotors, the turning action of the reactive torques is automatically eliminated — the main rotors turn in opposite directions and their reactive torques balance one another.
Main Rotor
With regard to the technique used to create and transmit torque, modern helicopters can be divided into two groups:
1) those with reactive drive;
2) those with mechanical drive.
In helicopters with reactive drive the engines are located at the tips
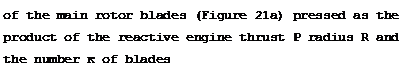
 In this case, the torque can be ex – hy the main rotor
In this case, the torque can be ex – hy the main rotor
V = P Rk.. tor eng
The torque balances directly the moment resisting rotation; therefore, the helicopter will not turn.
Characteristic for the helicopter with reactive drive are simplicity of its construction and low weight. It has no power expenditure to rotate a tail rotor, less vibration, and there is the possibility of obtaining high main rotor thrust with low thrust of the jet engine located at the tip of the blade.
Any type of reactive engine can be used as the reactive engine at the tip of the blade. However, at the present time the so-called compressor drive is most often used, i. e., reaction nozzles are located at the tips of the blades and are supplied with compressed air from a gas turbine engine or a special compressor.
The reaction-driven helicopter is still in the experimental stage. This is a result of difficult technical problems, the primary ones being:
a) reactive drive; b) mechanical drive;
1) engine gearbox; 2) main transmission shaft; 3) main rotor gearbox; 4) tail rotor d. riveshaft; 5) intermediate gearbox; 6) tail rotor gearbox.
high fuel consumption and low efficiency (2-3%) of the reaction drive;
complexity of the construction of the hub and blades, in which plumbing /27 must be provided;
complexity of the design of a reaction engine which will operate reliably when subjected to the high centrifugal force and the varying airstream direction;
deterioration of the aerodynamic characteristics of the main rotor owing to the engines located on the blades.
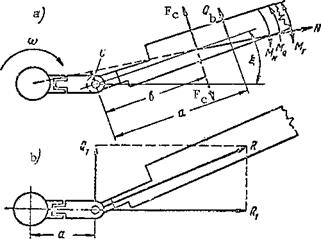
Helicopters with mechanical drive are those in which the torque transmitted from the engine to the main and tail rotors hy means of a special assembly, termed a transmission (Figure 21b).
The transmission includes the following basic units:
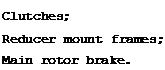 F. educers;
F. educers;
Shafts;
Shaft supports and connections;
Airframe-mounted engine reducers; Tail rotor reducers.
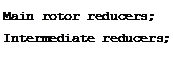 The main rotor reducer is provided to reduce the rotor shaft speed. The need for this reduction was explained above. Characteristic of this reducer is the high reduction ratio — from 1:8 to 1:14. Two-stage simple reducers are used on light helicopters; usually two-stage planetary reducers are used on the intermediate and heavy helicopters. The torque to the tail rotor is transmitted through the main rotor reducer. When the main rotor turns, the tail rotor is also automatically rotated. Thus, the main and tail rotors always constitute a single system and cannot rotate separately.
The main rotor reducer is provided to reduce the rotor shaft speed. The need for this reduction was explained above. Characteristic of this reducer is the high reduction ratio — from 1:8 to 1:14. Two-stage simple reducers are used on light helicopters; usually two-stage planetary reducers are used on the intermediate and heavy helicopters. The torque to the tail rotor is transmitted through the main rotor reducer. When the main rotor turns, the tail rotor is also automatically rotated. Thus, the main and tail rotors always constitute a single system and cannot rotate separately.
The intermediate reducers are installed in order to change the transmission direction (for example, at the juncture of the tail boom and the aft vertical fin). These reducers do not change the rpm., and consist of two conical gears.
The airframe-mounted engine reducers are used to transmit the torque from the horizontal engine shaft to the vertical transmission shaft. They are located in the engine case, and are used when the engine shaft axis is horizontal.
The tail rotor reducers are provided to transmit torque to the tail rotor /28 shaft and to reduce tail rotor shaft rpm. The mechanism for controlling the tail rotor is located in its reducer.
The torque is transmitted by the transmission shafts. The transmission of a single-rotor helicopter includes:
Main transmission shaft;
Tail rotor driveshaft.
The main transmission shaft transmits the torque from the engine to the main rotor reducer.
As a rule, the tail rotor driveshaft consists of several sections and transmits the torque from the main rotor reducer to the tail rotor reducer and Its length is 8-10 m. This shaft is a source of additional vibration of the helicopter.
All the transmission shafts rotate at high angular speed. Increase of the angular speed reduces the loading on the shaft for transmission of the same power.
The shaft supports prevent deflection and bending vibrations (whipping) of t. he long shafts. Ball bearings with elastic spacers are used as the supports. The shafts are connected with one another and with the other parts of the transmission by means of universals and flexible couplings; in addition to the interconnecting couplings there, are starting, engaging, and freewheeling clutches.
On some helicopters all three of these clutches are combined into a single, unit, located in the engine case together with the reducer. The freewheeling clutch is most frequently made in the form cf a separate unit. The starting clutch is a unit of the friction type and is intended for smooth connection of the transmission shaft with the engine shaft. When this type of connection is used, there is slippage of one shaft relative to the ether until the speeds of the driving and driven shafts become the same. This clutch transmits the small torque from the engine to the transmission when the engine is operating at low speed. The starting clutch provides smooth rotation of the main and tail rotors without jerking. When the transmission is engaged, the main clutch (most often of the dog type) is activated and connects the engine and transmission shafts rigidly together. The total torque is transmitted from the engine to the main and tail rotors through this
clutch. The freewheeling clutch is designed to transmit torque in one direction only — in the direction of rotation of the rotor. It provides automatic disconnect of the engine from the transmission if there is a reduction of the engine rpm. This is necessary in the main rotor autorotation regime if there is an engine failure in flight. Moreover, the presence of the freewheeling clutch leads to reduction of the inertial loads on the main rotor shaft when there is a change of engine operation. As a rule, the freewheeling clutch is located in the main rotor reducer case, between the main transmission shaft /29
and the reducer shaft. The main rotor brake is designed for rapid deceleration of the transmission after shutting down the engine on the ground.
The helicopter transmission is quite heavy, and therefore reduction of the weight of its individual components is of primary importance.











 Wi =
Wi =
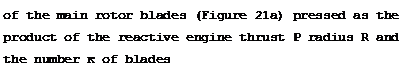
 F. educers;
F. educers; The main rotor reducer is provided to reduce the rotor shaft speed. The need for this reduction was explained above. Characteristic of this reducer is the high reduction ratio — from 1:8 to 1:14. Two-stage simple reducers are used on light helicopters; usually two-stage planetary reducers are used on the intermediate and heavy helicopters. The torque to the tail rotor is transmitted through the main rotor reducer. When the main rotor turns, the tail rotor is also automatically rotated. Thus, the main and tail rotors always constitute a single system and cannot rotate separately.
The main rotor reducer is provided to reduce the rotor shaft speed. The need for this reduction was explained above. Characteristic of this reducer is the high reduction ratio — from 1:8 to 1:14. Two-stage simple reducers are used on light helicopters; usually two-stage planetary reducers are used on the intermediate and heavy helicopters. The torque to the tail rotor is transmitted through the main rotor reducer. When the main rotor turns, the tail rotor is also automatically rotated. Thus, the main and tail rotors always constitute a single system and cannot rotate separately.