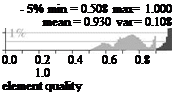
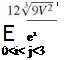The geometrical quality measure has to be defined for all element types used in TAU, and the choice has to consider the available information and experience about the relation between element shape and discretization error. The high aspect ratio of hexahedra or prisms for example is needed to simulate flows with anisotropic character. The analytic preliminary investigations also confirmed that the aspect ratio of quadrilaterals does not contribute to the element shape related discretization error in an otherwise regular grid.
Without a good reason not to do so the most simple measure is chosen for the unstructured part. A very simple and well known geometrical quality measure for simplices is the mean-ratio shape measure, e. g. [4]:
This is the ratio of the geometric and the arithmetic mean of the eigenvalues Xi of the linear transformation to the regular element. The resulting formulae for triangles (1) and tetrahedra (2) have a representation in terms of the element area A and the edge length a, b, c and in terms of the volume V and the edge length eij, respectively.
Most quadrilateral quality measures suggested in publications are derived from triangle quality measures such that high aspect ratios mean a low quality, e. g. [9]. So they are not applicable to TAU. Here another approach is tried. Instead of decomposing the quadrilateral and applying the triangle formula to the pieces, here the formula is decomposed and the parts interpreted as penalty terms of certain geometrical distortions. The analogue application to quadrilaterals shows how the term has to be modified to get a useful formula for TAU.
By means of the vector analysis the following representation of the mean-ratio quality for triangles can be found:
This can be considered as a decomposition of the mean-ratio quality into a term sin ф for the evaluation of distortion and a second term evaluating the stretching of the triangle. The stretching related term again has a mean ratio structure. It is the ratio of geometric and arthmetic mean of |tz| and | ^ | which are equal for a regular triangle. The decomposition into distortion and stretching depends on the choice of the triangle base side. This does not matter because the triangle formula will not be changed and the analogue formula for quadrilaterals which has to be changed will not depend on an arbitrary choice. Figure 7 shows the further proceeding.
The analogue formula considering distortion and stretching in the same way for quadrilaterals (4) does not include deviations from parallelism. So Q*uad can be considered as quality measure for parallelograms, see Fig. 7, middle part. In order to get a useful quality measure for TAU, the mean-ratio term evaluating the stretching is neglected and a term X for evaluation of the nonparallelism is added.
Fig. 7 Steps of derivation of the geometrical quality measure for quadrilaterals: interpretation as stretching and distortion (left), construction of the analogue measure for a parallelogram (mid) and addition of a term to evaluate the deviation from parallelism (right)
The choice of the term X is determined by the mean-ratio principle and the definition of a correct element quality measure. This includes that this measure is zero for a completely collapsed or otherwise distorted element. A measure is needed to evaluate elements of the TAU Code in a reasonable way. So an element has to be considered as completely distorted, if one of its triangle or tetrahedra parts collapses. The definition of X as the mean ratio, i. e. the ratio of geometric and arithmetic mean, of the triangle part areas meets both requirements, see Fig. 7, right part. The resulting quality measure for quadrilaterals Qquad can be expressed by formula (5).
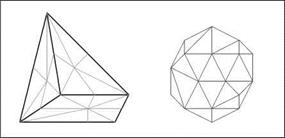
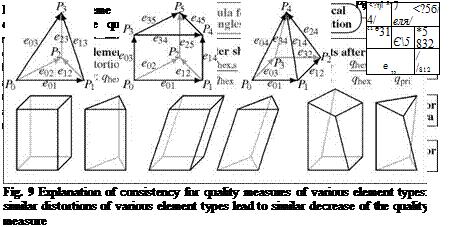
The application of this idea to the three-dimensional case includes a geometrical interpretation and a decomposition of the mean-ratio quality of tetrahedra. In this calculation the terms describing the base triangle can be replaced by the analogue terms for quadrilaterals, see Fig. 8, upper part. In this way a consistent quality measure for pyramids is derived. The quadrilateral quality can be generalized to hexahedra, considering the relation of triangle and tetrahedra quality. An application of this step to triangle bases leads to a quality formula for prisms, see Fig. 8, lower part.
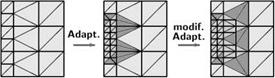
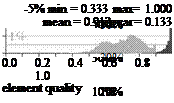
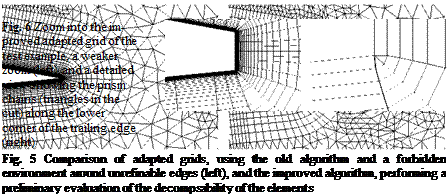
This procedure ensures a kind of consistency between the quality measures of various element types. In this context consistency means, that similar distortions applied to elements of various types lead roughly to the same decrease of the element quality for both element types, see Fig. 9.
This feature is very valuable for the use in adaptation algorithms. It could be used in the investigation of element subdivisions. For example, if a hexahedron of the structured layers is refined to bridging prisms, the prisms roughly inherit the quality of the parent hexahedron, and their quality is decreased by the horizontal stretching which was not relevant for the parent hexahedron. This decrease is nearly independent of the initial quality of the parent.
After all the needed calculation, we get the following formulae for the geometric quality measures of the various element types, equation (6)-(9). Figure 10 provides the notation of edges used in the equations.
Fig. 10 Notation of the edges of element types used in the formulae of geometric quality
with V0 — |e01, Є02 + Є12, Є03 + Є14 + Є251 ,••• and V01 — |e0b e02 + e12 + e35 + e45, e03 + e14| ^- ,
6v3 ^01,^03 + ^12,£4! • кз2+03+^1 2,-Е’4і ‘ koi + ^32+03,+4І • Qpyra = 3 ‘
+ ^32 )2 + 2(^03 + ^ 12 )2 + +4^ •
•коі+ез2,еі2,£4|) Г • ((еоі+^зг)2 + (Gb+^g)2) ‘ koi + ^321 • коЗ + ^12І with E4 — e04 + e14 + e24 + e34 ,
•коі + е32,^12,Д2І • к45+47 + ^5б,£’2І • • • • • 1+0 +03 +04 + ^371 • • • •
ІЕ0І • |+11 • 1+21
24
••• • |e01, E1, e04 + e15| • ••• • |e32 + e76, E1, e26| )
————————————————————– (9)
with E0 — e01 + e32 + e45 + e76 , E1 — e03 + e12 + e47 + e56 and E2 — e04 + e 15 + e26 + e37 •
The incomplete products in equations (7) and (9) go over all the tetrahedra parts of a prism and a hexahedron, respectively. The expression ^,y, z| — (x x y) • z denotes the triple product which can be calculated as a determinant of the vector entries.











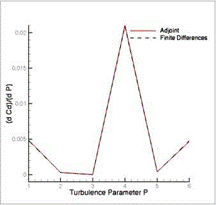



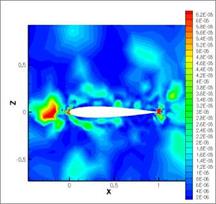
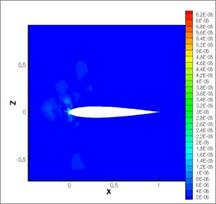
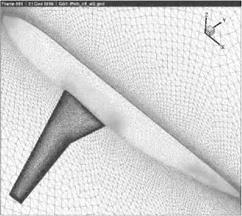
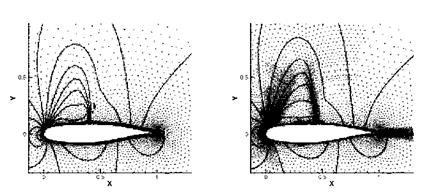
 NACA0012
NACA0012