Category MECHANICS. OF FLIGHT

But man has been to the moon – more than once – and has come back again; perhaps even more remarkable the Russians have sent spacecraft to the moon – without a man – have brought at least one back with samples, and have driven a moon-bug about on the surface! How has it been done? For the answer we must go back to circular and elliptical orbits. For a horizontal speed of launch of 10.46 km/s (just below the escape velocity), from a height of about 800 km, gives an elliptical orbit which will strike the moon, and at velocities of launch slightly above this, orbits will pass round both the earth and the moon (Fig. 13.12).

But the moon isn’t such an easy target as all that! The shape and size of the elliptical orbit is very sensitive to the exact direction and velocity of launch, and moreover the moon is itself travelling at rather over 3700 km/h, whereas the speed of the satellite at its apogee will only be about 700 km/h. Also, if the launch from the earth is made in an easterly direction – to take advantage of the earth’s rotation and consequent circumferential speed of 1600 km/h – the satellite at 700 km/h will be chasing the moon at 3700 km/h in the same direc­tion; so it will be a case of the moon hitting the satellite rather than the satellite hitting the moon – not that it matters which hits which, but it does mean that the satellite should be launched in the other direction and so approach the moon from the front, as it were, instead of chasing it.

In practice the initial launch must be made from ground level (Fig. 13B, overleaf), and not from an altitude of 800 km, and it has been calculated that if the satellite is guided only during the launching phase, and if the angle of launch is exactly correct, there must not be an error of more than 23 m/s in the launching speed of 11125 m/s; or if the velocity is exactly correct the angle of launch must be accurate to within 0.01°. If the satellite is to pass round the moon and the earth the accuracy must be even greater, so much so that some guidance after launch is a virtual necessity.

In view of the accuracy needed, not to mention the expense and man-power involved, it would be a mistake to imagine that flights to the moon or other planets have become, or are ever likely to become commonplace. None the less the experience so far gained has resulted in what might be called a standard procedure consisting of –

1. The launch to orbital height and speed.

2. One or more orbits of the earth.

Fig 13.12 Sending spacecraft to the moon Not to scale.

3. Rocket boost to required speed and direction for the moon.

4. Reverse burst of power to slow down, and put into orbit round the moon.

5. Separation of lunar module, and more reverse power to give a soft landing on the moon.

6. Lift-off from the moon, and into orbit to join up again with the command module.

7. Rocket boost to required speed and direction for the earth.

8. Reverse burst to slow down and put into orbit round the earth.

9. Re-entry, splash down and pick-up.

These phases have been described in detail in the Press, on radio and tele­vision, and in numerous articles and books; our purpose here is simply to indicate how the principles of mechanics apply to these various phases.

First then, the launch.

Now let us get just a little nearer to the true state of affairs by realising at least the existence of the moon. How will this affect the stone that is thrown verti­cally from the earth?

Fig 13.8 (a) a parabola, (b) a hyperbola

Fig 13.9 Conic sections

In (a) the plane cuts the cone at right angles to the centre line, forming a circle. In (b) the plane is at an acute angle to the centre line, but the angle is greater than a, forming an ellipse. In (c) the angle is egual to a, forming a parabola. In (d) the angle is less than a, forming a hyperbola.

Well, it will affect it quite simply, in principle at any rate, in that there will now be three masses all attracting each other – the stone, the earth and the moon.

The moon is about 385 000 km away from the earth. Just for the moment let us suppose that it remains over the point on the earth’s surface from which we throw the stone, and that we increase the starting velocity of the stone until it reaches distances of 6370 km, 12 740 km, and so on. As before, the weight will decrease with the distance from the earth’s surface, but now rather more so because a new factor has been introduced, the attraction between the moon and the stone. The mass of the moon is only about 1/81 of the mass of the earth, so the force of attraction at the same distance will only be a fraction of that of the earth (1/81 in fact), but as we know the moon’s attraction is a very real thing, even at the earth’s surface, for it is largely responsible for the tides.

We have already imagined so much that we may as well go one step further and imagine that our stone travels in a straight line between earth and moon. As it gets nearer to the moon the attraction of the earth will decrease and that of the moon increase, until a point is reached where the two attractions are the same. Since the force is inversely proportional to the square of the distance, the distance from the centre of the moon at which this occurs will be 1/V81 of the distance from the centre of the earth, or approximately one ninth (Fig. 13.10, overleaf); roughly say 39 000 km from the moon and 346 000 km from the earth. So if a stone is launched with just sufficient velocity to reach this point, it will stay there – and will once more be ‘weightless’, this time perhaps more correctly so, though again we notice that it is just a question of the forces being balanced. In fact the balance is too delicate, and the stone will not in fact stay at this neutral position, because some other heavenly body will attract it and tip the balance, and it will fall either onto the earth or the moon. If the stone is launched with a velocity slightly greater than that required to reach this neutral point, it will still be travelling towards the moon at this point, and since as it passes the point the attraction of the moon will become greater than that of the earth the stone will pick up speed and fall on to the moon.

It has already been emphasised that all bodies attract all other bodies, and that therefore one can never really escape from the gravitational attraction of all the bodies in the heavens. But the motion of a body in space becomes extremely complicated if the forces of attraction on it of even three bodies (such as the sun, the moon, and the earth) are taken into account, and for this reason it is convenient – and not very far wrong – to consider a zone of influ­ence for each body, this being a sphere in space in which that particular body has a greater gravitational effect than a larger body. The earth, of course, is well within the sun’s zone of influence – its motion round the sun is in fact con­trolled by the force of attraction between it and the sun – but on the other hand, bodies near the earth’s surface, although attracted by the sun, come much more under the influence of the earth’s attraction than that of the sun (which is perhaps just as well, since otherwise we would all be off to the sun). The attraction of the earth remains greater than that of the sun for a distance of about a million kilometres, so the earth’s zone of influence relative to the sun is a sphere of about one million kilometres radius (Fig. 13.11). Similarly the moon’s zone of influence relative to the earth is a sphere of about 39 000 km radius – as we discovered in the last paragraph, though we didn’t give it that name.

Well, we have described one way of getting to the moon – to go straight there in fact – but it is not quite so easy as it sounds because of the great accu­racy needed both in aim and launching speed. As regards aim, we have made

Fig 13.10 Neutral point between earth and moon

things much too easy in our imagination; in reality the earth is travelling round the sun, and is spinning on its own axis, while the moon is travelling round the earth. But even more interesting is the sensitivity to exact velocity.

The distance of 385 000 km to the moon is much less than the distance to infinity, only a minute fraction of it, and to the neutral point even less, but it requires nearly as much energy to reach this distance as it does to reach infinity because the attraction of the earth at this distance has been so reduced that nearly all the serious work in overcoming the earth’s gravity has already been done; or, putting it another way, whereas 11.184 km/s is needed to send the stone to infinity, about 11.168 km/s is needed to send it to the neutral point from which it will drop on the moon. So if launched at less than 11.168 km/s it will return to earth; at about 11.168 km/s it will go to the moon; at 11.184 km/s it will go to infinity (it could hit the moon on the way); and at over 11.184 km/s – well, we have mentioned that before.

The mass of the moon being so much less than that of the earth, its escape vel­ocity is only about 2.4 km/s, and that is the speed at which the stone would arrive on the moon if it ‘fell’ from infinity; it will for all practical purposes be the same if it falls the 39 000 km from the neutral point. This is about the muzzle

Fig 13.11 Zones of influence Not to scale.

velocity of a shell as it leaves a long-range gun, and so the landing on the moon will not be a very soft one, and this is the minimum speed at which the stone can arrive unless there is some means of slowing it down; there is no ‘atmosphere’ to do this, and the only hope is to break the fall by rockets fired towards the moon.

So much for circular orbits – now what about the elliptical orbits which, as we have already explained, are much more common for artificial satellites? They are also more common in nature, the orbit of the moon round the earth being one of the few examples of a nearly circular orbit.

Mathematically it is a little more difficult to calculate what happens during an elliptical orbit when both the velocity and the radius are constantly changing, but the reader who has followed the arguments so far should have no difficulty in understanding the principles involved. Returning to horizontal launches from a height of 800 km it will be remembered that at a speed of launch of 7.48 km/s the orbit was circular, below and above this speed it was elliptical, though at the escape velocity of 10.7 km/s it became an open curve, a parabola, and then above this a hyperbola. The real criterion is how much energy, kinetic energy, the body has when it is launched; because it is this energy which enables it to do work against the force of gravity – it is really much more like the case of the stone that was thrown vertically upwards than might at first appear. In vertical ascent the kinetic energy given to the body at the launch enables it to do work against gravity and so gradually acquire potential energy; at the highest point reached all the kinetic energy has become potential energy; then as the body falls again the potential energy is lost and kinetic energy regained until on striking the ground the original kinetic energy has all been regained (neglecting air resistance of course). The body travelling on a curved path also has to work against gravity, is also accelerating all the time, and downwards, just like the body on the vertical path, and in fact, at the same rate – once that is understood, all is clear.

The only difference then is that on curved paths the body must retain some of its kinetic energy throughout the circuit if it is to continue on its orbit. At a launching height of 800 km it has at the start both kinetic and potential energy; if the launching speed is less than the circular velocity of 7.48 km/s, but sufficient to ensure that it doesn’t come down to earth before reaching the far side, then by the time the body reaches the far side of the earth it will have dropped in height, i. e. lost some of its potential energy, but by the same token will have gained some kinetic energy (just like the falling stone), and so will be travelling faster – at over 7.9 km/s in fact if it is near the earth’s surface. Then as it returns to the starting point it will gain potential energy, rising again to 800 km, and lose kinetic energy, until the proportions (and values) are the same as they were at the launch. In all this we are still neglecting air resistance, and it is air resistance which in practice makes an orbit of this kind imposs­ible; for as soon as the body travelling round the earth, and getting lower all the time, meets appreciable air density, it will experience drag, and in working against this will lose kinetic energy and so the speed necessary to take it round the far side of the earth. Thus it will fall to the ground before getting half way round or the heat generated by kinetic heating will cause it to burn up.

As the launching speed gets nearer the circular velocity, the body will keep clear of appreciable atmosphere all the way round, and the orbit becomes more practical. But until the circular velocity is reached the launching point will be the apogee, and the perigee will be on the far side of the earth, where the body will be nearer the earth’s surface, and where the velocity will increase until, at the circular velocity, it remains constant all the way round.

As the launching speed is increased above the circular velocity, the body will have more kinetic energy than is necessary to keep the 800 km of height, and so it will gain height and potential energy, at the same time losing speed and kinetic energy, until it passes round the far side of the earth – now the apogee – at lower velocity and greater height. And so it will go on as the launching speed is still further increased, the ellipse becoming more and more elongated, the apogee getting farther and farther from the earth, and the residual velocity at the apogee getting less and less.

As the launching velocity approaches the escape velocity of 10.7 km/s, the body at the apogee will only just have sufficient kinetic energy to enable it to get over the top, as it were, and return again to earth. If launched at the escape velocity, or above, it won’t even be able to do this, and it will go off into space on its parabola, or hyperbola as the case may be, at the mercy of the gravita­tional attraction of some other body, probably the sun. This new force of attraction will restore its kinetic energy and velocity as it embarks on a com­pletely new orbit, possibly of enormous size like that of the earth round the sun (radius of orbit about 150 million kilometres).

Since nearly all practical orbits are in the form of ellipses it is interesting to consider some of the properties of these curves. The reader may know that an ellipse can be drawn on paper with a pencil and a piece of string of fixed length attached to two pins (Fig. 13.7, overleaf). In other words, an ellipse is the locus of a point moving so that the sum of the distances from these two points (the pins) is constant. These points are called the foci of the ellipse – in a circle, which is only a particular case of an ellipse, they coincide – and it will be noticed that in the figures illustrating the paths of satellites the centre of the earth is always one of the foci of the ellipse.

At launching speeds below the circular velocity the centre of the earth is the focus farthest from the launch, at the circular velocity it is of course the centre of the circular orbit, and at higher launching speeds it is the focus nearest to the launch, the other focus getting farther and farther away as the launching speed is increased. For launches at the escape velocity the distant focus has gone to infinity, and only one focus is left at the centre of the earth – a para­bolic curve has only one focus. Above the escape velocity, too, the hyperbolic

curve has only one focus (see Fig. 13.8); strictly speaking, a hyperbola has two foci, but this is because there are two parts of the curve, back to back as it were, and we are here only concerned with one part of the curve.

It is not of practical importance in understanding the mechanics of projec­tiles and satellites, but it may be of interest to know that these curves are all derived from a cone (they are the intersections of a plane and the surface of a cone) and are sometimes called ‘conic sections’ (Fig. 13.9).

As already established the velocity for a circular orbit is given by the formula – VL2 = gr2!d

where r is the radius of the earth, and d the distance from the centre of the earth.

At the earth’s surface d = r

V2 = gr-

Can the escape velocity be calculated equally simply? Very nearly so. If we go back to the idea of a body being projected vertically from the earth’s surface with sufficient kinetic energy to enable it to do work against the force of grav­itation all the way to infinity, then if the escape velocity is denoted by the symbol ve the

1

kinetic energy of a mass m will be ^inve

This kinetic energy must be sufficient to provide the energy needed to lift m from the earth’s surface to infinity. At a particular height above the earth, the energy needed to lift m one more metre is equal to its weight which equals mg at the earth’s surface, and decreases all the way to infinity when it will be zero. Since the weight changes and since the change is not a simple ratio but inversely as the square of the distance, it needs the principles of calculus to estimate the total work done, but the answer is very simple; it is the same as the weight at the earth’s surface mg X the radius of the earth, i. e. mgr.

but V* = gr

v =v X V2

e c

i. e. Escape velocity = V2 X Velocity of circular orbit at that radius.

Thus there is a simple relationship between all escape velocities and all circular velocities at a given radius from a mass such as that of the earth, or moon, or sun – the escape velocity is 1.41 X the circular velocity, or 41 per cent more.

So much for the story of what happens – what is the explanation of it all? In the particular case of the circular orbit the satellite is very like a stone on the end of a string stretching from the centre of the earth to the satellite; the satel­lite is all the time trying to go off at a tangent but is being given an acceleration towards the centre by the centripetal force which is of course the force of gravity. So, near the earth’s surface, if we neglect air resistance, the centripetal force will be the weight of the satellite, and the acceleration towards the centre will be 9.81 m/s2. Notice that a body circling the earth is accelerating towards the centre at the same rate as a body falling straight towards the earth. So we can easily calculate the circular velocity near the earth’s surface because the acceleration = v2lr (see page 14).

Now r is the radius of the earth, say 6370 km (6 370 000 m), so v2lr = g, i. e. iP-!6 370 000 = 9.81

Vі = 62 490 000 v = 7905 m/s = 7.9 km/s approx = 28 440 km/h approx

How long will the satellite take to make a complete circuit of the earth at this speed?

Circumference of earth = 2.к X 6370 km

So time of circuit at 28 440 km/h

= (2n X 6370)/28 440

= 1.41 hours or about

1 hour 25 minutes

It will be noticed that the circular velocity we have calculated, i. e. 7.9 km/s, is higher than the circular velocity at 800 km from the earth’s surface, i. e. 7.48 km/s; but there is no mystery in that and we can easily work it out for our­selves by replacing the earth’s radius of 6370 km by 7170 km, and reducing g by 20 per cent, i. e. to about 7.85 m/s2. The value of v1, and so of v, will then be less because whereas the value of g is reduced by 20 per cent, the value of r is only increased by 12y per cent – this, in turn, is because the value of g depends on the force of gravity, which is inversely proportional to the square of the distance r.

And what will be the time of a complete circuit at 800 km from the earth’s surface? The distance is greater, the speed less, so the time of orbit will be greater. Work it out and you will find that it is about 1 hr 40 min. Similarly at 1600 km the circular velocity is about 6.9 km/s and the time of orbit nearly 2 hours.

A distance of 35 400 km from the earth gives a particularly interesting cir­cular orbit because the time of a complete circuit is 24 hours; so a satellite travelling at this speed – in the right direction, of course – remains over one spot on the earth; a communication satellite such as is used for transmitting TV and radio signals from one part of the earth to another.

Then at about 385 000 km the circular velocity is a mere 3700 km/h (just over 1 km/s), and the time of orbit 28 days – but on that circuit we already have a satellite that surpasses in many ways any so far launched by man – the moon.

And now we can answer an obvious question – why doesn’t the moon fall on to the earth? Because it is revolving round the earth at just such velocity and radius that the centripetal force is provided by the gravitational attraction, in other words, in a sense it is ‘weightless’ – and this applies to all those bodies in orbit, whether circular or not, and to all the people and things inside them. Strictly speaking they are not weightless at all; in fact it is their weight, the force of attrac­tion between them and the earth (or moon) which they are orbiting, that keeps them in orbit and prevents them from going off at a tangent. They merely seem to be weightless, and that is why a man can get out of a space-ship while in orbit, and continue in orbit himself, just like the space-ship, without any fear of ‘falling’ back to earth or to anywhere else. Although he may be travelling at several kilometres per second he has no sense of speed, and apparently no weight – he just floats, and has no difficulty in keeping near the space-ship which is also just floating! More correctly the man, and the space-ship, and all the other things in orbit, are falling freely, are accelerating towards the earth because of the attraction of the earth – in short because of their weight – so much for weightlessness! In the same sense the moon is falling towards the earth, though it never gets any nearer!

Notice that the reader can calculate all these circular velocities and times of orbit for himself, including that of the moon. For at all distances from the centre of the earth, the condition for a circular orbit is that the acceleration towards the centre shall be the ‘g’ or acceleration of gravity at that distance; this we might call gd, and it must be equal to v2ld.

But gd is also proportional to the force of gravity, which is inversely pro­portional to the square of the distance.

Since at the earth’s radius r, the acceleration is g,

gd will be g X r2/d2

Therefore for circular velocity at any distance d, v2!d = g X r2/d2 i. e. v2 = gr2/d.

Figure 13.6 (overleaf) shows circular orbits at different distances from the centre of the earth.

It shows how a whole system of bodies can circle the earth, of their own free will as it were (once they have been put in orbit), and how the farther out the orbit the slower is the speed. It rather reminds one of the way in which Sir James Jeans once described the solar system as being like the traffic in Piccadilly Circus, with ‘the traffic nearest the centre moving fastest, that farther out more slowly, while that at the extreme edge merely crawls – at least by comparison with the fast traffic near the centre.’[10] But there is an important distinction between the solar system – the work of nature – and bodies orbiting the earth – the work of man (except for the moon); in the solar system, again to quote Sir James Jeans, there is only ‘one-way traffic’, and the orbits of the planets round the sun are mostly circular, or very nearly so, whereas the man-made satellites orbit the earth in various directions and, as we shall soon discover, some of their paths are very far from circular.

When talking of the interesting possibilities of a 24-hour circuit we men­tioned the direction of rotation. This would be all important in this case because if the satellite was rotating round the equator in the same direction as the earth’s rotation it would stay over the same spot on the earth’s surface but if it was travelling in the opposite direction – well, what would it do? Would it go twice round in a day? or would it merely appear to do so? or what?

But the fact that the earth is rotating will of course affect all launches, because it means that we are launching from a moving platform. The surface of the earth at the equator is travelling at a speed of rather over 1600 km/h owing to the spin of the earth on its axis, so a body launched in the same direc­tion, i. e. towards the east, will already have the advantage of this speed and so will need 1600 km/h less extra speed to achieve circular velocity, escape vel­ocity, or whatever it may be. Towards the west it will need 1600 km/h more extra speed. There can also be circuits of the earth in other planes altogether,

Fig 13.6 Circular orbits at different distances from centre of the earth Note. The speed at 35 400 km radius, and the speed and time of orbit at 20 000 km radius, have been left for the reader to work out for himself.

e. g. over the poles, and in these cases the effect of the earth’s rotation on launching and orbiting is more complicated.

It is not always realised, and it is interesting to note, that since the earth’s surface at the equator is travelling at about 1600 km/h all bodies on the earth are in a sense trying to be satellites, and to go straight on instead of following the curvature of the earth. Thus there are two reasons why a body of the same mass weighs less at the equator than at the poles, first because it is farther from the centre of the earth so the true gravitational attraction is less, and secondly, because a proportion of the gravitational force has to provide the centripetal acceleration. How much is this centripetal force? Is it appreciable? Well, work it out for yourself. Take the actual velocity as 1690km/h, the radius of the
earth as 6370 km, g as 9.81 m/s2, and you will find that the centrifugal force on a mass of 1 kg is about 0.018 N.

Among the many assumptions so far made one of the most impracticable has been the idea of leaving the earth’s surface at speeds of about 11 km/s.

But we all know the answer to this problem now, and it lies in rocket propulsion; by this means the acceleration is so comparatively gentle that it can even be withstood by human beings, at any rate in the lying down pos­ition.

When we consider the use of rockets to propel bodies to great heights or into a space a new complication is introduced in that owing to the great rate of fuel consumption the very mass of the projectile decreases rapidly, so we have the double effect of mass decreasing with fuel consumption and weight decreasing with distance from the earth. Moreover, in multi-stage rockets, which are the only practical means of achieving the velocities required for launching into space, there is a further decrease in mass each time a stage is completed and a part of the rocket is detached. The final mass that becomes a satellite, or goes off into space never to return, is but a small fraction of the mass at take-off.

In the interests of fuel economy turbojets, or better still ramjets, may be used for the flight of projectiles while they pass through the earth’s atmosphere, but in space rockets are the only means of powered propulsion, and all jour­neys in space are dependent on rockets and the law of universal gravitation.

In order to get our ideas straight we have so far considered the motion of missiles in a straight line – straight up and down from the earth’s surface. We did the same thing in Chapter 1 in dealing with ordinary mechanics, but then we graduated to the much more interesting motion on curved paths; this is what we are going to do now.

What happens if instead of throwing the stone vertically we throw it hori­zontally? – still neglecting the effects of air resistance.

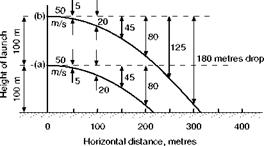
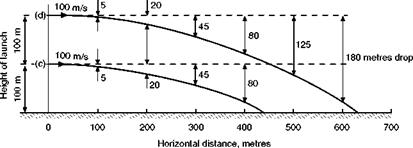
It will start with no vertical velocity, but will immediately begin to acquire a downward velocity at the rate of roughly 10 m/s2 – meanwhile it will retain its horizontal velocity. After 1 sec it will have fallen about 5 m, after 2 sec 20 m, and so on. If its initial horizontal velocity was 100 m/s, and if it was launched from a height of 30 m, its path of travel would be something like (a) in Fig. 13.3, or if it was launched from twice the height, like (b). If its initial horizontal velocity was 200 m/s, its path of travel would be more like (c) or (d) respectively.

It will be quite clear from these figures that the distance it will travel over the ground before striking the ground depends on the height at which it is pro­jected, and the horizontal velocity with which it is projected (the velocity being more important than the height). If it is projected at ground level it won’t get any distance before hitting the ground whatever its horizontal velocity; on the other hand, if it is projected from considerable height, and at a considerable horizontal velocity, it will travel a considerable distance horizontally before reaching the ground. The path of flight, or trajectory, is a mathematical curve called a parabola.

But now we have been guilty of making yet another assumption – has the reader noticed it? In the figures, and in our reasoning, we have assumed that the earth is flat. Not just that it is free of hills and dales (these won’t affect its flight path but they may obviously affect the point at which it hits the ground), but that the earth is itself a flat plane instead of being spherical or very nearly so. Such an assumption has no practical significance in the flight of stones or

Fig 13.3 Bodies launched horizontally – paths of flight
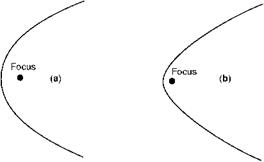
cricket balls – but is all-important in the flight of high-speed projectiles. The curvature of the earth will affect the path of the projectile, and the distance it travels before striking the ground, for two reasons – first, because if the pro­jectile didn’t ‘fall’ towards the earth it would go off at a tangent and so get farther and farther away; secondly, because although the force of gravity acting on the body is always ‘vertical’ in the sense that it is always towards the centre of the earth, the direction of the vertical will change in space and this will change the shape of the curve – in mathematical terms it means that the trajectory is an ellipse rather than a parabola. These effects are shown in the figure (Fig. 13.4) – hopelessly exaggerated of course in the case of a stone or cricket ball, or even an ordinary shell fired from an ordinary gun, but not by any means exaggerated for modern rocket-propelled high-speed ballistic mis­siles and not, in this figure, even going as far as the man-launched satellite or space-ship.

It should now be clear that the greater the speed with which a projectile is launched from a given height above the earth’s surface in a horizontal direc­tion, the larger will be the curve it describes and so the greater will be the distance it travels before it hits the surface; in other words, the greater will be the range.

The actual range, of course, depends on the direction of launch as well as the speed and height but at first it is easier to consider only horizontal launches. And by ‘launching’ we mean that the projectile is given a velocity and then left to itself – and so becomes subject to the mechanics of ballistics. If it continues to be rocket-propelled almost anything may happen!

If we take ‘launch’ to have this meaning, then the launch conditions can be achieved at the end of the ‘launch cycle’ involving, usually, rocket propulsion between the earth’s surface and the launch point where the rocket is switched off and the body left to the mercy of ballistics.

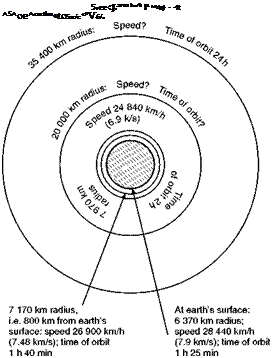
Tet us assume then that we are launching a projectile horizontally from a height of 800 km above the earth’s surface. This besides being a nice round figure is well outside any appreciable effects of the earth’s atmosphere, and although it is even farther beyond the ceiling of ‘aeroplanes’ it is within the reach of multi-stage rockets. To those of us who are accustomed to think of heights in thousands of feet or metres it sounds a great height (eight hundred

Fig 13.4 Path of projectile – curved earth

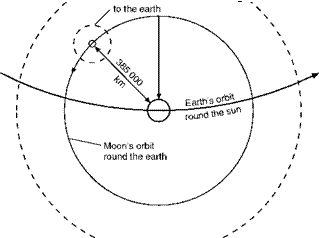
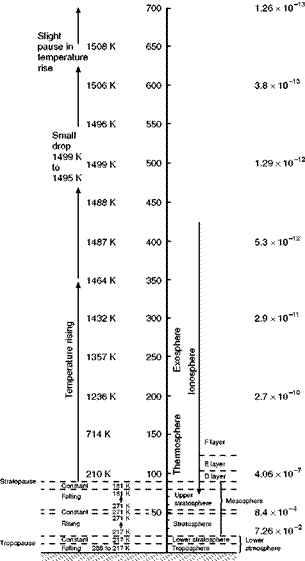
thousand metres), but in terms of space travel it is practically nothing, only one eighth of the radius of the earth away from the surface, about one four hundred and eightieth of the distance to the moon, and one hundred thou­sandth of the distance to the sun. At this height the weight of a body and the acceleration due to gravity are reduced by about 20 per cent of what they were at the earth’s surface.

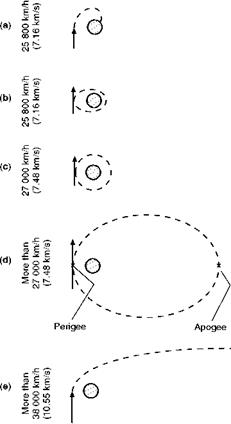
So much then for conditions at our launching platform, let us now see what happens as we increase the velocity of a horizontal launch. At first the projec­tile will simply get farther and farther round the earth, but always coming down to earth again at some point less than half way round (Fig. 13.5a, over­leaf). Then at a certain velocity (about 7.16 km/s or 25 800 km/h) a most exciting thing will happen (or at least it would happen if it were not for our old enemy air resistance) – the projectile will just miss the surface on the far side of the earth and will then gain height again, and, perhaps most exciting of all, will circle the earth and come round to where it started – and will then repeat the performance – and so on. The projectile has become a satellite – it is travelling round the earth under its own steam as it were (Fig. 13.5/?).

Unfortunately it can never happen quite like this because although it was clear of air resistance at the launch, on the far side it would have come right through the atmosphere to ground level and so would burn up owing to the heat created or, even if it could be shielded in some way from this, it would lose speed and fall to the earth.

But we have only got to increase the launching velocity a little further and the projectile will then miss the far side of the earth by an appreciable margin, and when this is say 300 km, it will miss most of the atmosphere and so con­tinue to circle the earth on an elliptical orbit, clearing it by 800 km on one side and 300 km on the other – in any such orbit the point at the greatest distance from the centre of the earth is called the apogee, and the point nearest the centre of the earth the perigee. Our projectile is now a practical satellite – prac­tical, but still not very probable.

Even at a height of 300 km there is some atmosphere, and there probably is even at 800 km for that matter, so this satellite will lose speed every time it dips into the atmosphere, and so will gradually lose the energy given to it at the launch and will sooner or later come down to earth on a spiral path.

But we need not be disheartened, because a further increase of launching speed will further increase the clearance on the far side, and so gradually elim­inate this problem until, at a launching speed of about 7.48 km/s we reach another interesting stage at which the satellite – we can no longer call it a pro­jectile – travels round the earth on a circular path, 800 km from the earth’s surface, and there is no longer any distinction between the apogee and the perigee (Fig. 13.5c). The launching speed at which this occurs is called the cir­cular velocity.

After this long story the reader will probably be able to guess what happens with further increase of launching speed. Yes, the circle again becomes an ellipse but the apogee, or farthest point, is now on the far side of the earth and

Fig 13.5 Earth satellites

Speeds refer to horizontal launches from 800 km above the earth’s surface, in the interests of clarity this distance has been exaggerated in comparison with the radius of the earth.

the perigee is the point of launch (Fig. 13.5d). Still further increases of speed make the ellipse more and more elongated with the apogee getting farther and farther from the earth. It will not be difficult to understand why this type of orbit is frequently used; it practically eliminates the problems of air resistance, it is not dependent on an exact launching speed and it allows scope for travel at the apogee to great distances and so, for instance, for passing beyond the moon or other planets, or hitting them.

Is this the end of the story? Not quite. Strange as it may seem the ellipse cannot be stretched indefinitely, and at a launching speed of about 10.7 km/s – different speeds at different heights – the ellipse becomes an open curve, a parabola, and the satellite travelling on this open curve escapes from the earth for ever, and becomes a satellite of the sun (Fig. 13.5e). Yes, this is the escape velocity again, and it only differs numerically from the previous one because we are now launching from 800 km instead of from ground level. So the escape velocity is the highest velocity at which a body can be launched in any direction and be expected either to orbit the earth or return to it again – above that speed, speaking vulgarly, we have had it. Above that speed, too, the path of travel changes from a parabola to a different open curve called a hyperbola, but this is a subtle change for a subtle reason, and it need not worry us.

This is not quite the end of the story as at even higher speeds there comes a point where the object can escape from the solar system and carry on out into space indefinitely.

Consider a stone thrown vertically from the earth’s surface with an initial vel­ocity. Because the weight of the stone, caused by the gravitational attraction between the stone and the earth, opposes the stone’s motion its velocity will be reduced with time (i. e. the stone has an acceleration g towards the earth). With a normal initial velocity gravitational acceleration will stop the stone at a certain height above the earth’s surface and it will then reverse direction and accelerate towards the earth, eventually arriving at its launch point with its launch velocity but in the reverse direction (if air resistance is neglected).

For moderate initial velocity it is sufficiently accurate to assume that the weight (and hence g) is constant. What happens, though, if the initial velocity is large enough for a great height to be reached before the stone’s direction of travel is reversed?

The weight of the stone, in accordance with the law of gravitation, is inversely proportional to the square of the distance between the masses. So supposing that the stone has a mass of 1 kilogram it will, at the surface of the earth, have a weight of 981 N. But what if it is moved away from the earth’s surface altogether? What if it is thrown upwards 1 kilometre, 100, 1000, 6000 kilometres? Let us pause here for a moment because the radius of the earth is not much more than 6000 km, 6370 km in fact, so at a distance of 6370 km from the earth’s surface, the force of attraction, i. e. the weight of the stone, being inversely proportional to the square of the distance from the centre of the earth – now doubled – will only be 1/4 of its weight at the earth’s surface; similarly, at 12 740 km it will be 1/9, at 19 110 km only 1/16, and so on (see Fig. 13.2). Notice that in the figure the distances are given from the centre of the earth, and not from the earth’s surface; for the earth is a very small thing in space, and if we are to understand the mechanics of space we must think more and more of the mass of the earth as concentrated at its centre.

The mass of the stone of course does not change, but as the weight changes so also does the acceleration (g) in proportion – this is just Newton’s Second Law again. So the rate at which the stone loses speed on the outward ‘flight’, though starting at 9.81 m/s2, gets less and less as the distance from the centre of the earth increases. This makes it more difficult to calculate how far the stone will go with a given starting velocity, but it has an even more interesting and important effect than this. For think of the stone returning to earth again; at great distances the rate at which it picks up speed will be very small, but the rate will increase until at the earth’s surface it reaches the definite and finite value of 9.81 m/s2. This, it will be noticed, is a maximum rate of increase, and it can be shown mathematically that even if the stone starts from what the mathematicians call infinity (which means so far away that it couldn’t come from any farther!) the velocity reached will also have a definite and finite maximum value, which is in fact 11.184 km/s (about 40 250 km/h). So, if a stone is ‘dropped’ onto the earth from infinity, it will hit the earth at 11.184 km/s; and, by the same token, if it is thrown vertically from the earth at 11.184 km/s it will travel to infinity – and never return. This velocity is called the escape velocity. If it is thrown with any velocity less than this, it will return.

What happens if it is thrown from the earth at a velocity greater than the escape velocity? Or is this not possible? Yes, it is not only possible, but in a sense it has been done though not quite in this simple way. And all that happens is that it still has a velocity away from the earth when it reaches infinity – and so will go beyond infinity – but since infinity is the limit of our imagination perhaps it will be best to leave it at that. The reader may have noticed that to simplify things, we have only considered the earth’s attraction on the stone, and the rest of the universe has been left out! But still the prin­ciple is illustrated.

It is important to remember that although the force of gravity, the weight of the stone, gets less and less as it travels farther and farther from the earth it never ceases altogether (at least not until the stone reaches infinity which is only another way of saying ‘never’). It is often stated, quite incorrectly, that ‘escape’ from the earth means getting away from the pull of the earth. This we

Fig 13.2 How weight varies with height R = radius of earth, i. e. approx. 670 km

can never do, the earth ‘pulls’ on all other bodies wherever they are – that after all, is the universal law of gravitation. Why then do astronauts talk about ‘weightlessness’? – and even demonstrate it? – we shall soon see.

In the meantime, it will be noticed that we have already introduced a new unit of velocity, the kilometre per second. Our reason for this is simply one of convenience; in this part of the subject we have to deal with very high speeds, and it is easier to remember these speeds, and even to think what they mean, as kilometres per second, than as so many thousands of knots, or metres per second. At the same time we must remember that our old friend g is still in m/s2, so if we wish to use any of the standard formulae of mechanics we must be careful to convert the velocities into metres per second.

Now let us consider the motion of bodies in this upper atmosphere, and in the space beyond.

If we throw a stone or cricket ball up into the air it goes up to a certain height, stops, and then comes down again. If we throw it vertically upwards it comes down on the same spot as that from which we threw it and, if we neglect the effects of air resistance, it returns with the same velocity down­wards as that with which we threw it upwards. Moreover, again neglecting air resistance, we can easily calculate how high it will go because we know that (at first, at any rate) it loses velocity as it travels upwards at the rate of 9.81 m/s or, very roughly, lOm/s every second, and gains it again at the same rate as it comes downwards.

But we ought to know better by now than to neglect air resistance? Yes, we certainly ought to know better, but unfortunately it wasn’t only air resistance that we were neglecting in the simple examples in Chapter 1 – though, in fair­ness, that was our worst error, and our other omissions really were negligible in the circumstances that we were then considering. This is no longer true of the circumstances of this chapter for some of which air resistance really can be neglected, but other things that we calmly assumed most certainly cannot.

Newton would probably have been less surprised than we were when arti­ficial satellites began to circle the globe – for these are but examples of the laws he enunciated.

When he saw the apple drop – assuming that story is true – he wondered why it did so, and eventually decided that it was because there was a mutual force of attraction between the apple and the earth; so it wasn’t just a case of the apple dropping, it was the apple and the earth coming together, due to this mutual force of attraction, when there was no longer anything to hold them apart. And if the apple and the earth, why not any mass and any other mass? And so eventually, by observing the facts, and by reasoning, he came to realise that there is a force of attraction between any two masses, and that this force is proportional to the product of the masses, and inversely proportional to the square of the distance between them. This is the law of universal gravitation, perhaps the most important of all the physical laws, the law that governs the movement of bodies in space (whether they be natural or artificial), the law that Newton enunciated 300 years ago.

At first glance it may seem that space flight (Fig. 13A, overleaf) is purely con­cerned with ballistics and is completely divorced from aerodynamics, but as we hinted in Chapter 1 at the speeds and heights of modern flight aeroplanes behave to some extent like missiles, and missiles, given the required thrust and speed, can actually become satellites. Moreover, both missiles and artificial satellites must pass through the earth’s atmosphere when they are launched, and there experience aerodynamic forces, and – what is far more important – the most hopeful means of returning them safely to earth again is to use aero­dynamic forces to slow them up and control them.

In short, the subjects of aerodynamics, ballistics, and astronautics have merged into one subject, the mechanics of flight, and no apology is needed for the inclusion of this chapter in a book on that subject.

The upper atmosphere

The atmosphere with which we have been concerned in the flight of aeroplanes – i. e. the troposphere and the stratosphere – is sometimes called the lower atmosphere; the remainder is called the upper atmosphere (Fig. 13.1, overleaf).

In the lower atmosphere the temperature had dropped from an average of + 15°C (288 K) at sea-level to —57°C (217K) at the base of the stratosphere, and had then remained more or less constant. The pressure and density of the air had both dropped to a mere fraction of their values at sea-level, about 1 per cent in fact. One might almost be tempted to think that not much more could happen, but such an assumption would be very far from the truth.

There is a lot of atmosphere above 20 km – several hundred kilometres of it, we don’t exactly know, it merges so gradually into space that there is really no

Fig 13A Shuttle lift off (By courtesy of NASA)

exact limit to it – but a great deal happens in these hundreds of kilometres. The temperature, for instance, behaves in a very strange way; it may have been fairly easy to explain its drop in the troposphere, not quite so easy to explain why it should then remain constant in the stratosphere, but what about its next move? For from 217 К it proceeds to rise again – in what is called the mesosphere – to a new maximum which is nearly as high as at sea-level, perhaps 271K; then, after a pause, down it goes again to another minimum at the top of the mesosphere. Estimates vary of just how cold it is at this height (only 80 kilometres, by the way, only the distance from London to Brighton), but all agree that it is lower than in the stratosphere, lower, that is to say, than anywhere on earth, perhaps 181К ( —92°C). But its strange behaviour doesn’t stop at that and, once more after a pause at this level, as the name of the next region, the thermosphere, suggests, it proceeds to rise again, and this time it really excels itself rising steadily, inexorably to over 1200 К at 200 km, nearly 1500 К at 400 km, and still upward in the exos­phere until it reaches over 1500 К at the outer fringes of the atmosphere.

Fig 13.1 The upper atmosphere

The figures given are based on the US Standard Atmosphere, 1962, which was prepared under the sponsorship of NASA, the USAF and the US Weather Bureau.

An interesting point about these temperature changes in the upper atmos­phere is their effect upon the speed of sound which, as we learned in Chapter 11 , rises with the temperature, being proportional to the square root of the absolute temperature. The interest is not so much in the effects of this on shock waves, or on the flight of rockets, but rather in that one method of esti­mating the temperatures in the upper atmosphere is by measuring the speed of sound there.

While these strange and erratic changes of temperature have been taking place the density and the pressure of the air have fallen to values that are so low that they are almost meaningless if expressed in the ordinary units of mechanics; at a mere 100 km, for instance, the density is less than one-mil­lionth of that at ground level.

It is believed that at these heights there may be great winds, of hundreds, perhaps even a thousand kilometres per hour. The air above about the 70 km level is ‘electrified’ or ionised, that is to say it contains sufficient free electrons to affect the propagation of radio waves. For this reason the portion of the atmosphere above this level is sometimes called the ionosphere, which really overlaps both the mesosphere and the thermosphere. Then there are the mys­terious cosmic rays which come from outer space, and from which on the earth’s surface we are protected by the atmosphere, but beyond this we know very little about them except that they may be the most dangerous hazard of all since they affect living tissues. Then there are the much more readily under­standable meteors, ‘shooting stars’ as we usually call them, but actually particles of stone or iron which have travelled through outer space and may enter the earth’s atmosphere at speeds of 100 kilometres per second, and which have masses of anything from a tiny fraction of a gram up to hundreds of kilograms. The larger ones are very rare, but some of these have actually survived the passage through the atmosphere without burning up, and have ‘landed’ on the earth causing craters of considerable size – these are called meteorites.

To prospective space travellers all this may sound rather alarming, but there are some redeeming features. The winds, for instance, wouldn’t even ‘stir the hair on one’s head’ for the simple reason that the air has practically no density, no substance. For the same reason the extreme temperatures are not ‘felt’ by a satellite or space-ship (what is felt is the temperature rise of the body itself, caused by the skin friction at the terrific speeds; it is this which burns up the meteors, it is this which has eventually caused the disintegration of many man – launched satellites on re-entering the atmosphere – but all this has little or nothing to do with the actual temperature of the atmosphere). Then, as regards the very low densities and pressures, no-one is going to venture outside the vehicle, or walk in space, or even put his head out of the window to see whether the wind stirs the hair on his head, unless he is wearing a space-suit, and we have long ago learned to pressurise vehicles because this is required even for the modest heights in the lower atmosphere. Moreover, the strong outer casing of the vehicle which is required for pressurising will in itself give protection at least from the small and common meteors, and to some extent even from the cosmic rays, the greatest unknown. So altogether the prospect is not as bad as it might at first seem to be.

So far as aeroplanes are concerned, the North American X15 was quoted in an earlier edition of this book as the nearest approach to a piloted hypersonic aircraft – indeed, if we accept M5 as the threshold of hypersonic flight, it was hypersonic for it achieved a speed of 1860 m/s and a height of 95 940 m as long ago as 1962 – this speed corresponds to a Mach Number of over 6. It was launched from a mother craft at 13 720 m and 224 m/s; it had a rocket engine giving a thrust of 260 kilonewtons, and rocket nozzles for space control, but fuel for only 68 seconds at full power. It landed, as an aeroplane, at 134 m/s some 320 kilometres from launch.

The experimental programme with the X15 has now been superseded by a similar programme with what are called lifting bodies, with little if anything in the way of wings, with powerful control surfaces and, as their name implies, with bodies so shaped as to give a certain amount of lift at high speeds. As with the X15 these are launched from a mother craft, have rocket power avail­able for a very limited period, and this can be used first to attain considerable height and then, after a fast and steep descent – usually without power – towards the earth, a circling approach at some 15 m/s for the last 6000 m or so, followed by a steep glide, using speed brakes as required, and finally a touch of rocket power to help the round out, and a fast landing at about 100 m/s.

These lifting bodies offer some advantages for future shuttle and sub orbital vehicles.

1.

For solutions see Appendix 5.

For numerical questions on flight at transonic and supersonic speeds see Appendix 3.

Fig 12E Another supersonic configuration

The McDonnell Douglas F-18 Hornet which features a wing with only moderate rearward sweep on the leading edge, and a small forward sweep on the trailing edge. The sharply swept strakes also generate lift, and control the flow over the main wing.