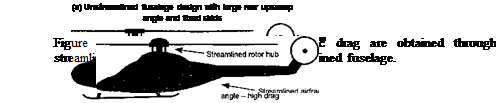
The fuselage is the largest airframe component on a helicopter, so its aerodynamic characteristics will have a significant impact on the performance of the helicopter as a whole. Functional constraints such as the need for rear loading doors means that the shapes that are typical of helicopter fuselage designs are often prone to flow separation and high drag. In addition, the airframe often operates in the main rotor wake, which changes the aerodynamic characteristics compared to those obtained without the rotor. These effects make the understanding and prediction of airframe aerodynamics extremely complicated, to the point that the whole of Chapter 11 is devoted to the subject.
6.6.1 Fuselage Drag
The parasitic drag of the fuselage affects cruise speed and fuel consumption of the helicopter. Williams & Montana (1975) and Keys & Wiesner (1975) have emphasized the need for low fuselage drag in the design of helicopters for improved performance. The drag of a helicopter fuselage may be up to one order of magnitude higher than that of a fixed-wing aircraft of the same gross weight. One reason is because of the rotor shaft, hub, and blade attachments, which may account for 30% or more of the total fuselage drag – see Sheehy & Clark (1975) and Sheehy (1977). Another major contributor is the fuselage after-body or bluff-body drag, which may account for 20% of the total fuselage drag. Drag is also caused by flow separation in the region where the main fuselage tapers to the tail boom. Sedden (1982) has shown that large drag penalties result when using fuselage shapes with large rear fuselage upsweep angles, because these can promote flow separation and
 |
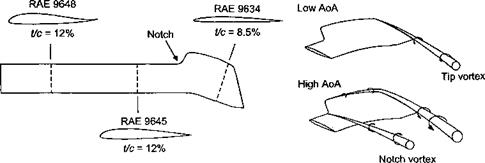
the formation of two strong trailing vortices. See also Epstein et al. (1994) for details of this phenomenon.
There are, however, many constraints that can limit the design of the fuselage shape and consequently the lowest possible drag of the fuselage. Much depends on the operational needs for the machine. For example, as shown in Fig. 6.24 an executive transport helicopter can be designed to have a more streamlined fuselage compared to a utility helicopter, which may need to have a rear access door. In either case, it is found that the fuselage shape should be more circular than square to keep drag as low as possible. Using a fairing over the top of the fuselage can help reduce drag from the main rotor shaft and control linkages. See also Montana (1975,1976). Replacing the skids with a retractable undercarriage can reduce drag considerably. However, a fixed wheeled undercarriage will have higher drag than skids. The use of active flow separation control concepts seems a prime candidate for a future means of fuselage drag reduction – see Section 9.12.
In view of the complicated interacting viscous dominated flows that can exist over helicopter fuselages, predictive capabilities for pressure and skin friction drag are not yet mature. Current capabilities for design are based on synthesis of component drag using experimental data or by using a combination of experimental data and potential flow theory. Classical panel methods have found considerable use in routine helicopter fuselage design – see Section 14.7 for details. These methods are based on the assumption of small disturbance potential flow, with the basic approach being described by Hess (1990). A modem treatment
|
|
Plotkin (1991). Large computer codes that use panel methods are commercially available and are in widespread use in the helicopter industry. Sophisticated computational fluid dynamics methods such as Navier-Stokes and Reynolds-Averaged Navier-Stokes (RANS) are still in the development stage – see Section 14.2.1. Even if enormous computer memory and storage requirements can be overcome, they are relatively far from being practical for use in routine helicopter fuselage design studies. Another problem with Navier-Stokes methods is the efficient generation of grids, and especially the proper coupling of structured and unstructured grids. However, rapid progress in grid generation techniques and solution
algorithms is being made. See, for example, Berry et al. (1994), Chaffin & Berry (1994), Duque & Dimanlig (1994), and Duque (1994).
To supplement numerical predictions of fuselage aerodynamics, semi-empirical drag prediction methods are in widespread use in the helicopter industry. Based on component testing in the wind tunnel, and with some additional engineering judgment, these approaches can give very reliable estimates of fuselage drag. An estimate of the fuselage parasitic equivalent wetted or flat-plate area, / (introduced in Section 5.4.5), can be determined from a knowledge of the drag coefficients of the various components that make up the helicopter using an equation of the form
 (6.28)
(6.28)
where Sn is the area on which the definition of Co is based. This may be either the wetted area or the projected frontal area of the component. Initial drag estimates will assume no mutual interference effects from individual components, but despite this approximation the approach is found to give a reasonable initial estimation for the fuselage drag. More refined values of / are obtained by component testing of isolated fuselage and rotor/fuselage models in the wind tunnel – see, for example, Bosco (1972), Wilson (1984), Philippe et al. (1985), and Wilson (1990). Component interference effects can then be incorporated into the drag estimate. Further refinements need actual flight tests because wind tunnel models cannot simulate accurately the effects of full-scale Reynolds numbers, or drag producing details such as antennas, leakage through doors, and other gaps. In this case, estimates of drag are derived indirectly from rotor power measurements. The whole process, although somewhat empirical, gives quite reliable estimates of the parasitic drag.
An analysis of the individual items contributing to the parasitic drag of a typical helicopter is given in Table 6.1. These results are not for any one helicopter design per se and must be considered only as representative. It will be apparent that a major source of the overall drag is the rotor hub and blade attachments, which may account for up to 30-50% of the total parasite drag on fully articulated rotor blade designs. Sheehy & Clark (1975), Sheehy (1977), Sedden (1979), and Prouty (1986) give a good summary of various sources of published rotor hub drag data. Considerable turbulence may also be produced behind the hub, which
Table 6.1. Typical Breakdown of Parasitic Drag
Components of a Representative Helicopter.
Afte r Prouty (1986)

 Component
Component
Fuselage
Nacelles
Rotor hub & shaft Tail rotor hub Main landing gear Tail landing gear Horizontal tail Vertical tail
Rotor/fuselage interference Exhaust system Miscellaneous
|
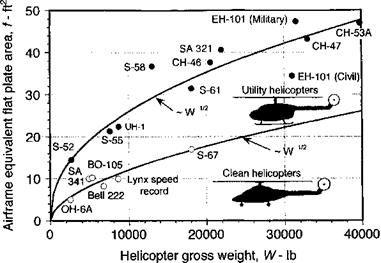
Figure 6.25 Equivalent flat-plate (wetted) areas for a selection of helicopter designs.
|
can have an influence on the magnitude and frequency of the airloads produced on the tail boom and empennage; see Berry (1997) for a discussion of hub turbulence measurements. Further discussion of this important issue is made in Chapter 11. Streamlining the fuselage on the top of the airframe near the hub can help reduce the drag of the rotor shaft, the exposed controls, and the hub. However, it is only with the use of modem hingeless or bearingless rotors that hub drag reductions are possible, with values of f j A for a bearingless rotor being about half those of an articulated design. Cler (1989) describes a fully faired hub design, although this is impractical for most helicopters.
The equivalent total flat-plate areas of helicopter airframes range from less than 10 ft2 (0.93 m2) on smaller helicopters to as much as 50 ft2 (4.65 m2) on large utility helicopter designs, as shown in Fig. 6.25. Heavy-lift crane designs may have twice these values (>100 ft2 or 9.3 m2 being typical). The measured data have been obtained from a variety of sources, including Rosenstein & Stanzione (1981). The results suggest that values of f/A typically will fall between 0.004 for clean helicopter designs and up to 0.025 for first-generation or heavy-lift transport helicopters. Again, notice that the drag curves are approximately proportional to (weight)1/2, which follows the “square-cube” law mentioned previously. Obviously, the addition of external hardware or stores on military helicopters tends to dramatically increase its equivalent wetted area, thereby significantly increasing power required and reducing forward flight performance. Conversely, a general drag clean up of the airframe can result in substantial increases in climb and forward flight speed capability, as well as in reduced fuel bum and improved overall operational economics.












 (6.28)
(6.28)