Category The Art of the Helicopter

Centre of mass, the point at which the mass of the body appears to be concentrated

Fig. 2.1 At (a), the distributed mass of a body can be replaced by a point mass acting at the centre of mass (CM). The mass centroid (b) is a line joining the centres of mass of thin slices through the body.

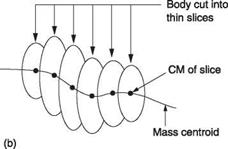
of gravity (CG) will also be found, but this is incorrect as objects still have a centre of mass in the absence of a gravitational field. If a body is imagined to be divided into a series of slices, each slice will have a CM. Figure 2.1(b) shows that the line joining all of these CMs is known as the mass centroid. The location of the mass centroid is important in blade design and in balancing rotating assemblies.

The speed of an object is the rate at which it covers distance, and the direction is immaterial. In contrast, velocity is the rate at which distance is covered in a specific direction. Any quantity that also has direction is called a vector. Acceleration is the rate of change of velocity, so it must be a vector. Acceleration can come about by keeping the direction the same and changing the speed, or by keeping the speed the same and changing the direction. The force necessary to change velocity is equal to the mass multiplied by the acceleration:

F = m x a

In SI units, the unit of force is the Newton (N). This is defined as the force that will cause a mass of one kilogram to accelerate at one metre per second per second.

On the surface of the earth, a mass of 1 kg experiences a gravitational attraction of about 9.81 N. Consequently any object released at a height will accelerate down­wards at 9.81 metres per second per second. This downward acceleration, commonly called falling, can be prevented by opposing gravity with an upward force of 9.81 N. Figure 2.2(a) shows what happens. The object is supported by upward force opposing its weight. Clearly force is a vector quantity. When the two forces are exactly equal and opposite, the object is in equilibrium: the resultant force and the acceleration are both nil.

Consider an elevator in a high-rise building. When the elevator starts, the motor applies a greater upward force to the occupants than gravity applies downwards.

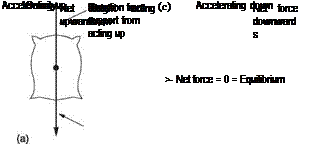Cable tension

Fig. 2.2 Weight is the force a body exerts on its supports. At (a) the weight is equal to the supporting force and there is no resultant. At (b) upward acceleration requires a greater force than in (a) so the weight appears to increase. At (c), downward acceleration causes weight to reduce. Note that the mass does not change, but the weight does.

Figure 2.2(b) shows that there is no longer a balance of forces, so there is no equilibrium. The difference between the force of gravity and the greater force from the floor of the elevator accelerates us upwards. We feel the extra load on our feet: temporarily our weight has increased. As the elevator approaches the desired level, the motor will reduce power, and the force it applies will be less than that due to gravity. Figure 2.2(c) shows that the resultant force is now downwards, and our ascent is slowed until we stop. Momentarily our weight is reduced: we feel light on our feet. Note that as the elevator slows we are going upwards but accelerating downwards. There is no contradiction here; acceleration is the rate of change of velocity.

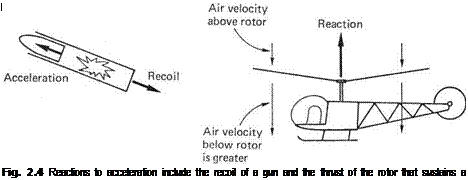
Figure 2.3 shows what happens to an object having mass when forces act on it to accelerate and decelerate it. As there is always a reaction to the application of a force, if force is applied to an object in order to accelerate it, the reaction will attempt to accelerate whatever is supplying the force the opposite way. Figure 2.4 shows some examples. The recoil of a gun is the reaction to accelerating the shell. The thrust of a ship’s propeller is the reaction to accelerating water backwards. A helicopter stays airborne by accelerating air downwards: the reaction is upwards, and if it is equal to the force due to gravity, the helicopter is in equilibrium. Note that the helicopter is not weightless, its weight is acting on the air around it as the substantial downwash indicates.

‘ Force

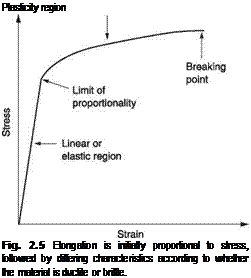
In aircraft, various forces must be resisted by the structure. The ability of a material to resist forces is measured with respect to unit cross-sectional area, typically a square metre. The force applied per unit of area is known as the stress. Figure 2.5 shows that as the force applied to unit area increases, initially there will be a proportional elongation according to Hooke’s Law. The elongation per unit length is known as the strain. The constant of proportionality is known as the stiffness. In the linear region, the material recovers its dimensions when the stress is removed. If the stress is further increased, the strength of the material may be exceeded and an irreversible extension, known as plasticity, may take place, leading finally to breakage. In brittle materials, the plastic region may be negligibly small.

A structure that can resist a given static load may eventually suffer fatigue failure if the load is repeatedly applied and removed. In practice a safety factor must be applied to the maximum stress and the life of the component may be restricted to a certain number of cycles. Fatigue primarily occurs in parts under tensile stress, probably because this condition encourages the spreading of cracks. Highly stressed components

such as rotor heads may need extremely fine finishing and surface treatment to minimize any irregularities from which a crack might propagate. Periodic inspection of highly stressed parts may be needed. Cracks can be detected by X-rays, ultrasonic testing or by penetrating dyes. At high temperatures, materials working within their elastic limit may creep if the load is sustained. This phenomenon limits the life of turbine blades.

In many cases it is not the ability of the component to resist the load that matters, but the amount of deflection the load is allowed to cause. Unwanted deflections are generally unwelcome in aircraft as they may result in flutter or imprecise control. Consequently stiff materials are advantageous. All aircraft have to lift themselves as well as any payload, so it is an advantage if the weight of the structure can be minimized. It is often thought that this will be achieved using low density materials, but this is not always the case. In practice the lowest weight will be achieved by using materials with a high stiffness to relative density ratio. This ratio also controls the speed of sound in the mate­rial, which is generally high in aerospace materials as can easily be established by tap­ping them. The result is a sound of a higher pitch than that found in everyday materials. Such materials also make good loudspeaker cones, where the same criteria apply.

In practice the designer would like to have a range of materials all having high stiffness to relative density ratio, but with a range of relative densities and strengths. Where stresses are concentrated, a high strength, high density material is used. Where stresses are reduced, a lower density material will be superior. For example, if a component were made from an excessively strong material, the thickness required to carry the design load might be so small that the component might suffer handling damage. Honeycomb and foam cored materials are one approach to reducing density. In a helicopter, the density of materials used tends to fall with distance from the rotor axis.

Earlier in this chapter, the forces were either up or down in order to introduce one concept at a time. In the real world forces can act in arbitrary directions, except for the

force due to gravity, which doggedly remains pointed downwards. When several forces are acting, it is possible to find out what happens by determining the direction and magnitude of the resultant force.

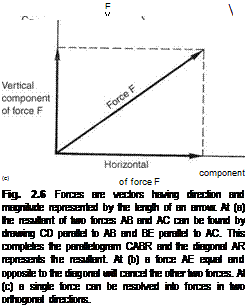
Figure 2.6 shows how forces are represented. An arrow is drawn in the direction of each force, and the length of the arrow is proportional to the magnitude. In this case two different forces act on the same point, and in different directions. We can find the resultant force, which is a single force having the same effect as the others together, by completing the parallelogram as shown, and drawing in the diagonal. The body will accelerate in the direction of the resultant. Alternatively, by drawing a force of equal length to the resultant but in the opposite direction, we have found the force needed to maintain equilibrium with the other two.

The opposite of finding a resultant to two forces is splitting a single force into two different ones. This is known as resolving, and the two forces are known as components. It is common to resolve an arbitrary force into horizontal and vertical components. The figure shows that it is easy to do. Horizontal and vertical lines are drawn from both ends of the force arrow. The intersection of the lines shows the magnitude of the horizontal and vertical components of the force.

So far only forces that all conveniently act at one point have been considered. In reality forces can also act at a distance from a point. When a force does not pass through a point the result is called a moment with respect to that point. The moment is equal to the force multiplied by the distance at right angles to the force, as shown in Figure 2.7. Applying a moment to an object will cause it to turn and accelerate along simultaneously.

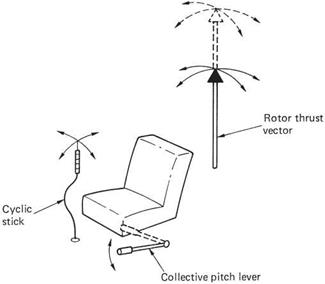
If two equal and opposite forces act a distance apart, the result is a pure turning effort known as a couple or as torque. A helicopter engine produces a couple at the output shaft in order to drive the blades. The reaction to this couple attempts to twist the engine against its mountings. The transmission conveys the engine power to the rotor shaft. The rotor shaft exerts a couple on the rotor head in order to drive the blades round. The torque reaction to this couple attempts to rotate the transmission, and the helicopter hanging from it, the opposite way. One of the jobs of the designer is to find a means to prevent this rotation.

When a body is supported at the CM, it will remain in the initial attitude. Figure 2.8 shows that if the support is not at the CM, the body will rotate. It may swing from side to side, but eventually will come to rest with the CM below the point of support.

It is often assumed that the CM of the helicopter is below the rotor shaft, but this may not be the case. Figure 2.9 shows how a helicopter hovers with the CM displaced. The CM tends to hang directly beneath the rotor head, and the pilot has to displace the cyclic control in order to keep the disc horizontal so the rotor thrust vector is straight up. Clearly if the CM is a long way from the mast, a substantial amount of cyclic control will be used up to compensate, and there may not be enough left to control the machine. In addition the bearings and joints in the rotor head find it harder to transmit power when the shaft and the disc are not aligned.

Force F

Moment arm, I

Moment = F x I Units = Nm, ft. lbs Resultant force = F

Force offset = I

Couple = F x I Units = Nm, ft. lbs Resultant force = F – F = zero

(b)

Fig. 2.7 (a) A moment about a point is the product of the force and the distance. (b) A pure couple results from two equal and opposite forces that do not coincide.

Fig. 2.8 (a) A body supported at a point not above the CM will swing until the CM is below the support as in (b).

For all these reasons, the CM position of a helicopter is important. Taking on passengers, fuel and payload can move the CM of the machine. It is the responsi­bility of the commander to ensure that the CM of the helicopter is within the limits laid down by the authorities for the machine in question.

In everyday speech these terms are used with a variety of meanings, but in mechanics their meanings are much more closely defined. Work is done when a resultant force moves through a distance. A table supporting objects placed on it does no work on them because although there is a force holding them up, there is no movement. A crane lifting an object does work because the force of gravity is opposed throughout the distance the load is lifted.

Energy is a measure of the ability to do work. Sometimes the interchange between work and energy is reversible. Burning fuel releases energy that allows an engine to do work. This is not reversible. A wound-up spring holds the energy that drives a clock. A helicopter battery holds enough energy to start the engine. These are both
reversible. Work is done winding the spring or charging the battery and this is turned into stored energy, most of which can later be released to do work.

Energy can also be stored in the position and motion of objects. If a weight is lifted against gravity, it stores potential energy that can be released when the weight is lowered again. Potential energy is proportional to the height through which the object is lifted. If a weight is accelerated, the resultant force acting on it moves through a distance and does work which is stored as kinetic energy. Figure 2.10 shows a mass being accelerated from rest by a constant force F over a distance s in time t up to a velocity v. The kinetic energy of the mass is equal to the work done on it. This is equal to the product of force F multiplied by distance s.

Since F = m x a, then KE = m x a x s.

Acceleration is the rate of change of velocity, thus a = v/t. Since the velocity increases uniformly then distance s is the time multiplied by the average speed, thus s = 1 v x t.

v v ■ t m ■ v2

KE = m x a x s = m x – x =

t 2 2

Kinetic energy is proportional to the square of the velocity. Power is the rate at which work is done or the rate at which energy is released, which is the same thing. Thus a high powered engine will burn fuel at a higher rate in order to release more energy in a given time.

The final quantity to be considered is momentum. This is equal to the mass multiplied by the velocity. The use of momentum will better be explained when the topic of lift generation is dealt with in Chapter 3.

A helicopter in flight has both kinetic and potential energy. This energy was stored in the helicopter by doing work against the earth’s gravitational field. Thus the heli­copter’s potential and kinetic energy exists with respect to the earth and Newton’s laws determine what the helicopter will do with respect to the earth when forces act upon it. The earth is the inertial frame of reference.

Other than gravity, the forces when airborne can only come from the movement of the machine and its rotors with respect to the air. In still air the aerodynamic frame of reference and the earth’s frame of reference are the same and this simplifies matters. However, when considering a machine flying in the presence of a wind, it is important to realize that the wind means that the aerodynamic frame of reference is moving with respect to the inertial frame of reference.

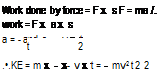The reader is cautioned against texts that erroneously claim that the helicopter flies only with respect to the air because it doesn’t know what the ground is doing and that all that matters is airspeed. If this were true artificial horizons and inertial navigators wouldn’t work.

Fig. 2.10 A mass being accelerated will gather kinetic energy (KE) as derived here.

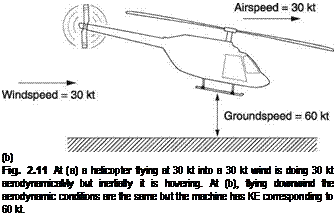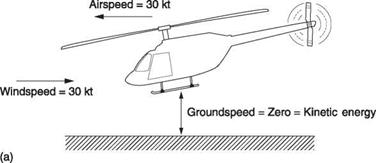
Figure 2.11(a) shows a helicopter flying at 30 knots directly into a 30 knot wind. Aerodynamically it is doing 30 knots but inertially it is stationary and has no kinetic energy. Inertially it is hovering. Figure 2.11(b) shows a helicopter flying at 30 knots down wind in a 30 knot wind. Aerodynamically the conditions are the same, but iner­tially the machine is now doing 60 knots and possesses the kinetic energy due to that groundspeed. The difference in kinetic energy becomes obvious when an attempt is made to change heading. If the helicopter in (b) does a 180° turn, it will conserve its kinetic energy and will exit the turn with 60 knots of groundspeed and 90 knots on the ASI. The result will be that the machine will tend to climb as the surplus airspeed is converted to potential energy.

If the helicopter in (a) tries a 180° turn it will be in difficulty and will lose height because it lacks 60 knots worth of kinetic energy. If the machine isn’t powerful and doesn’t have height to lose it could crash. And the pilot who thought that the helicopter doesn’t know what the ground is doing wouldn’t know what he did wrong.

Efficiency is generally defined as the ratio of useful output power to input power in any mechanism. In the case of a gearbox the useful power is the output shaft power. This will always be less than the input power and the difference will be converted to heat.

In the case of an engine, the input power is the heat released by burning the fuel. In practical engines, this exceeds the output shaft power considerably. The percentage of the thermal energy in the fuel that emerges as shaft power is the thermal efficiency of the engine. The waste heat has to be removed by a cooling system to prevent the temperature of the engine rising to the point where components are damaged. Cooling systems waste further power in driving fans and pumps and usually increase the drag of the airframe.

Given the necessary high power to weight ratio in helicopters, the power plant and fuel form a significant part of the all-up weight. It is beneficial to explore means to improve the thermal efficiency of the engine. Not only will this reduce the weight of the fuel to be carried for a given range, but it may also allow the cooling system to be lighter, to consume less power and to cause less intake drag. Thus a small improvement in thermal efficiency may result in a significant increase in performance.

Passenger aircraft may be compared using specific air range (the mass of fuel used per unit of distance), but in a hovering helicopter this figure is meaningless. In helicopters, it may be better to compare the power actually used to hover with the theoretical power needed by an ideal rotor under the same conditions.

The atmosphere is the medium in which helicopters fly but it is also one of the fuels for the engine and the occupants breathe it. It is a highly variable medium that is constantly being forced out of equilibrium by heat from the sun and in which the pressure, temperature, and humidity can vary with height and with time and in which winds blow in complex time – and height-variant patterns. The effect of atmospheric conditions on flight is so significant that no pilot can obtain qualifications without demonstrating a working knowledge of these effects.

The atmosphere is a mixture of gases. About 78% is nitrogen – a relatively unreactive element – whereas about 21% is oxygen, which is highly reactive. The remainder is a mixture of water in the gaseous state and various other traces. The reactive nature of oxygen is both good and bad. The good part is that it provides a source of energy for life and helicopters alike because hydrocarbons can react with oxygen to release energy. The bad part is that many materials will react with oxygen when we would rather they didn’t. Chemically, combustion and corrosion are one and the same thing. The difference is based on the human reaction to the chemical reaction.

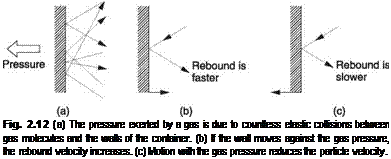
Gases are the highest energy state of matter, for example the application of energy to ice produces water and the application of more energy produces water vapour. The reason that a gas takes up so much more room than a liquid is that the molecules contain so much energy that they break free from their neighbours and rush around at a high speed, which is a function of absolute temperature. As Figure 2.12(a) shows, the innumerable elastic collisions of these high speed molecules produce pressure on the walls of any gas container. In fact the distance a molecule can go without a collision, the mean free path, is quite short at atmospheric pressure. Consequently gas molecules also collide with each other elastically, so that if left undisturbed, in a container at a constant temperature, every molecule would end up with essentially the same energy and the pressure throughout would be constant and uniform.

Pressure is measured by physicists and by engineers in units of force per unit of area using imperial units of pounds per square inch or SI units of Newtons per square metre. At sea level, the atmosphere exerts a pressure of about 15 pounds per square inch and has a density of about 0.075 pounds per cubic foot or in metric units about

100 000 Newtons per square metre with a density of 1.225 kg per cubic metre. Over the years, many other units of pressure have evolved, some from meteorology. One of these is the bar (after barometry) where one bar is the average atmospheric pressure at the place where the bar was defined. In practical use, the bar is divided into one thousand millibars. The bar is slowly being replaced by a numerically identical unit known as the hectoPascal (hPa). The bar and hPa are commonly used in aviation altimetry. The principle of the mercury barometer is that atmospheric pressure supports a column of mercury exposed to a vacuum at the top. Consequently the length of the column is proportional to pressure and can be expressed in inches or cm of mercury. At sea level a reading of about 26 inches of mercury is obtained. This unit may be found in use in altimeters originating in the United States.

The Gas Law states that the product of pressure and volume is proportional to temperature. Reducing the volume means that external work has to be done to oppose the pressure. This work increases the temperature of the gas. The Diesel engine obtains ignition in this way. Conversely if the volume is increased, work is done by the expansion of the gas and the temperature must fall. This is why carburettors are prone to icing on part throttle because the air expands on entering the manifold. Air conditioners work in the same way.

If the volume is fixed, as temperature rises, the velocity of the molecules increases and so the impact at each collision with the walls of any container is greater and the pressure rises. Alternatively the same pressure can be exerted in a given volume with a smaller mass of gas. Thus in the atmosphere where pressure increases can be released by free movement, the result of an increase in air temperature is that the density goes down. Density is also affected by humidity. Water molecules are heavier than those of atmospheric gases and increase the pressure due to molecular collisions. Thus in the presence of water vapour a given pressure can be sustained with a smaller mass of air and the density goes down.

Sound is simply an airborne version of vibration which is why the two topics are inextricably linked. Sound disturbs the equilibrium of a gas, as does the creation of lift. Not surprisingly, aerostats excepted, all flying objects make a noise as a by-product of creating lift. Consequently there is a great deal of overlap between aerodynamics and acoustics.

Figure 2.12(b) shows that a solid object that moves against gas pressure increases the velocity of the rebounding molecules, whereas in (c) one moving with gas pressure reduces that velocity. The average velocity and the displacement of all the molecules in a layer of air near to a moving body is the same as the velocity and displacement of the body. Movement of a body results in a local increase, or decrease, in pressure. Thus sound is both a pressure and a velocity disturbance. Integration of the velocity disturbance gives the displacement.

Despite the fact that a gas contains endlessly colliding molecules, a small mass or particle of gas can have stable characteristics if molecules leave and are replaced by others having identical properties. As a result aerodynamics and acoustics seldom need to consider the molecular structure of air and the constant motion can be neglected. Thus when particle velocity and displacement is considered in aerodynamics or acous­tics, this refers to the average values of a large number of molecules. In an undisturbed container of gas the particle velocity and displacement will both be zero everywhere.

When the volume of a fixed mass of gas is reduced, the pressure rises. The gas acts like a spring; it is compliant. However, a gas also has mass. Sound travels through air by an interaction between the mass and the compliance. Imagine pushing a mass via a spring. It would not move immediately because the spring would have to be com­pressed in order to transmit a force. If a second mass were to be connected to the first by another spring, it would start to move even later. Thus the speed of a disturbance in a mass/spring system depends on the mass and the stiffness. Sound travels through air without a net movement of the air.

After the disturbance had propagated the masses would return to their rest position. The mass/spring analogy is helpful for a basic understanding, but is too simple to account for commonly encountered acoustic phenomena such as spherically expanding waves.

Unlike solids, the elasticity of gas is a complicated process. If a fixed mass of gas is compressed, work has to be done on it. This will generate heat in the gas. If the heat is allowed to escape and the compression does not change the temperature, the process is said to be isothermal. However, if the heat cannot escape the temperature will rise and give a disproportionate increase in pressure. This process is said to be adiabatic and the Diesel engine depends upon it. In most acoustic cases there is insufficient time for much heat transfer and so air is considered to act adiabatically. Figure 2.13 shows how the speed of sound c in air can be derived by calculating its elasticity under adiabatic conditions.

у = adiabatic constant (1.4 for air)

R = gas constant (8.31 J K-1 mole-1) T = absolute temp (K)

M= molecular weight (kg mole-1)

Assume air is 21% 02, 78% N2, 1% Ar

Molecular weight = 21%x16x2 + 78% x 14 x 2 + 1% x 18 x1 = 2.87 x 10-2 kg mole-1

V= /1-4×8.31 T = 20 л VT

V 2.87 x 10-2

at 20°C 7= 293 К V= 20.1 V293 = 344 ms-1

Fig. 2.13 Calculating the speed of sound from the elasticity of air.

If the volume allocated to a given mass of gas is reduced isothermally, the pressure and the density will rise by the same amount so that c does not change. If the temp­erature is raised at constant pressure, the density goes down and so the speed of sound goes up. Gases with lower density than air have a higher speed of sound. Divers who breathe a mixture of oxygen and helium to prevent ‘the bends’ must accept that the pitch of their voices rises remarkably.

The speed of sound is proportional to the square root of the absolute temperature. At sea level the speed of sound is typically about 1000 feet per second or 344 metres per second. Temperature falls with altitude in the atmosphere and with it the speed of sound. The local speed of sound is defined as Mach 1.

As air acts adiabatically, a propagating sound wave causes cyclic temperature changes. The speed of sound is a function of temperature, yet sound causes a temperature variation. One might expect some effects because of this. Sounds below the threshold of pain have such a small pressure variation compared with atmospheric pressure that the effect is negligible and air can be assumed to be linear. However, on any occasion where the pressures are higher, a situation not unknown in aviation, this is not a valid assumption. In such cases the positive half cycle significantly increases local tempera­ture and the speed of sound, whereas the negative half cycle reduces temperature and velocity. Figure 2.14 shows that this results in significant distortion of a sine wave, ultimately causing a shock wave that can travel faster than the speed of sound until the pressure has dissipated with distance. This effect is responsible for the sharp sound of a handclap and for the sonic boom of a supersonic aircraft.

Whilst the hulls of helicopters do not approach the speed of sound, their rotor blade tips certainly do and the effects of this have to be taken into account. The drag on a rotor blade at moderate speeds increases as the square of the relative airspeed but as Mach 1 is approached the drag increases disproportionately; an effect called compress­ibility. This is intuitively understandable as the air has less time to get out of the way when the disturbances that propagate ahead of the blade are travelling a little faster than the blade itself. In extremely cold weather, or at high altitude, the speed of sound falls and helicopters with high tip speeds will suffer a loss of efficiency.

Sound can be due to a one-off event known as percussion, or a periodic event such as the sinusoidal vibration of a tuning fork. The sound due to percussion is called transient whereas a periodic stimulus produces steady-state sound having a frequency f.

Fig. 2.14 At high level, sound distorts itself by increasing the speed of propagation on positive half cycles. The result is a shockwave.

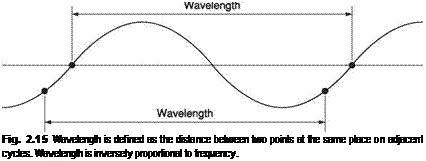Because sound travels at a finite speed, the fixed observer at some distance from the source will experience the disturbance at some later time. In the case of a transient, the observer will detect a single replica of the original as it passes at the speed of sound. In the case of the tuning fork, a periodic sound source, the pressure peaks and dips follow one another away from the source at the speed of sound. For a given rate of vibration of the source, a given peak will have propagated a constant distance before the next peak occurs. This distance is called the wavelength lambda. Figure 2.15 shows that wavelength is defined as the distance between any two identical points on the whole cycle. If the source vibrates faster, successive peaks get closer together and the wavelength gets shorter. The wavelength is inversely proportional to the frequency. It is easy to remember that the wavelength of 1000 Hz is a foot (about 30 cm) at sea level.

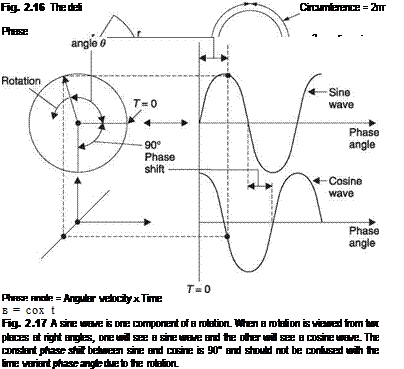
By definition helicopters contain a lot of rotating parts and for a proper understanding of their characteristics, knowledge of the mechanics of rotation is essential. In physics, the engineering quantity of RPM is not used. Instead the unit of angular velocity is radians per second and the symbol used is rn. Figure 2.16 shows that a radian is a natural unit of angle which is the angle subtended by unit circumference at unit radius. As the circumference is given by 2n times the radius, then there will be 2n radians in one revolution, such that one radian is about 57°.

Figure 2.17 shows a constant speed rotation viewed along the axis so that the motion is circular. Imagine, however, the view from one side in the plane of the rotation. From a distance, only a vertical oscillation will be observed and if the position is plotted against time the resultant waveform will be a sine wave. The sine wave is unique because it contains only a single frequency. All other waveforms contain more than one frequency.

Imagine a second viewer who is at right angles to the first viewer. He will observe the same waveform, but at a different time. The displacement is given by multiplying the radius by the cosine of the phase angle. When plotted on the same graph, the two waveforms are phase shifted with respect to one another. In this case the phase shift is 90° and the two waveforms are said to be in quadrature. Incidentally the motions on each side of a steam locomotive are in quadrature so that it can always get started (the term used is quartering). Note that the phase angle of a signal is constantly changing with time whereas the phase shift between two signals can be constant. It is important that these two are not confused. In a three-bladed rotor, the motion of each blade

would be phase shifted by 120° from that of the next blade, whereas the phase angle of a blade changes continuously as it rotates. In helicopters the phase angle is taken to be the angle between the blade and a line drawn directly aft from the rotor hub.

Geometrically it is possible to calculate the height or displacement of the sine wave in Figure 2.17 because it is given by the radius multiplied by the sine of the phase angle. The phase angle is obtained by multiplying the angular velocity rn by the time t. Frequency f is measured in rotations per second or Hertz (Hz). Thus the phase angle at a time t is given by at or 2nft.

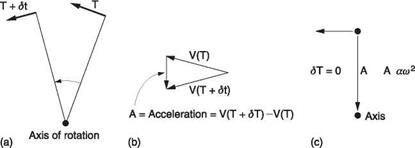
A rotating object is not in static equilibrium even if the RPM is constant. With the exception of those elements of the object which are on the axis of rotation, all other elements are in a constant state of acceleration because their velocity is constantly changing as they follow a curved path. Figure 2.18(a) shows that if an arbitrary incre­ment of time is taken, the velocity at the beginning is different from that at the end and a small resultant vector is necessary to close the triangle. As the time increment

Fig. 2.18 A body following a circular path is at constant acceleration and if this is calculated, it can be used to derive the forces acting. (a) shows that after a short time St, the velocity has changed direction. (b) The rate of change of velocity is the acceleration. (c) shows that if St is allowed to fall to zero, the acceleration points to the centre of rotation.

becomes vanishingly small this vector will be seen to point to the axis of rotation as can be seen in (c).

As the RPM increases, the length of the velocity vectors in Figure 2.18 increases in proportion to RPM, as does the angle between them. As the resultant for small angles is the product of the vector length multiplied by the angle between them, it is easy to see that the acceleration or rate of change of velocity is proportional to the square of the RPM. The advantage of the use of ш to measure angular velocity is that if this is done the velocity at any radius r is simply ш x r and the acceleration is simply ш2 x r. There are no constants or conversion factors to remember which is a major advantage of the MKS metric system.

It was shown above that F = m x a, it can be seen that the inward or centripetal (Latin: centre seeking) force needed to accelerate an object in a circular path is simply:

F = m x ш2 x r as ш = v/r then F = m x v2/r

When a mass moves along, or translates, it has kinetic energy. When an object rotates, it also has kinetic energy, but the amount is less easy to calculate. This is because all elements of a translating mass move at the same velocity, whereas in a rotating mass different elements move at different velocities according to how far from the axis they are. By adding up all of the kinetic energies of blade elements at different velocities, the kinetic energy of the rotor can be found. If an elemental mass Sm is rotating at radius r with angular velocity ш, its velocity is ш x r and so its kinetic energy must be:

Sm x ш2 x r2
2

An arbitrary body can be treated as a collection of such masses at various radii and the integral of the kinetic energies of all of these gives the total kinetic energy. If this is divided by the square of the angular velocity the result is the moment of inertia; the rotational equivalent of mass. Any rotating body could have the same moment of inertia if all of its mass instead were concentrated at one radius from the axis of rotation. This is known as the radius of gyration.

The rotor blade requires an inward or centripetal force to accelerate it into a circular path. Each element of the blade is at a different radius and so calculating the overall
force would be complicated were it not for the fact that the blade mass appears for this purpose to be concentrated at the radius of gyration. The figures for root tension are quite impressive. In a typical model helicopter a tension of 500 N is normal. In a full size helicopter 100 000 N is not unusual.

When a body of arbitrary shape is rotated, if the centre of mass is not on the axis of rotation, forces must come from the bearings to accelerate the CM into a circular path. This is the origin of vibration due to imbalance. In space no such forces can be applied and the only way the rotation can occur is for the CM and the axis to align. Thus rotating devices try to achieve such alignment and vibration results when bearings prevent it.

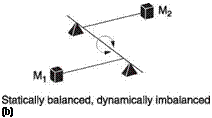
Figure 2.19(a) shows that a simple balancing process consists of supporting the assembly with the axis horizontal. If the CM does not coincide, gravity will turn the assembly until the CM is beneath. Balance weights may be added until the assembly will stay where it is left. In this condition the assembly is statically balanced, with no net moments, but it may still vibrate when rotated. Figure 2.19(b) shows that a statically balanced assembly can result with masses at different places along the axis of rotation. This will be imbalanced when rotating.

The statically balanced body in Figure 2.19(b) will try to rotate along its mass centroid. To eliminate vibration, the body must be dynamically balanced. This means

a *-i, . *~2 ,

■ A ————–

M1 A M2

Static balance: М1 x Ц = M2 x L2

(a)

Covering material

Fig. 2.19 Static balance (a) can be achieved when no overall moment results about the axis of rotation. (b) A statically balanced system that will vibrate when rotated as it is not dynamically balanced and will tend to turn about its mass centroid. (c) In model helicopters, dynamic balance is achieved by adding a small piece of covering material. The mass needed is equal to the difference in mass of the two blades, and the position is such that the blades balance in the same place.

that weights are added at various places along the axis to bring the CM of the slices onto the axis. When balancing car wheels, note that weights may be fitted both to the inner and outer rims to achieve this.

In the case of a helicopter rotor, the blades will be in the same plane and so the effects due to Figure 2.19(b) will be small. However, a statically balanced rotor could still be achieved if one blade were heavier than the other, if its CM were nearer the shaft. Thus to dynamically balance a rotor, it is necessary that all of the blades should have exactly the same mass, and the same radius of gyration. This means that the distribution of mass along and across each blade should be identical and the CM should be at the same point in three axes. In full size rotor blades, weight pockets are provided at various places to allow these conditions to be met.

In model helicopters dynamic balancing is just as important, but a simplified approach can be used. Figure 2.19(c) shows that the blades must be carefully weighed, and a piece of covering material is cut to have exactly the same mass as the difference in masses of the blades. The blades are assembled to the balanced rotor head, and the covering material is applied to the lighter blade at a point where static balance is achieved. It will then be found that the two blades have their CM in the same place and so the rotor will be dynamically balanced. The same result will be obtained if the cov­ering is moved until both blades balance in the same place. In full-size helicopters the leading edge of the blade may be protected with a replaceable plastic film. If part of this comes off or the film is not fitted identically to each blade, vibration may result.

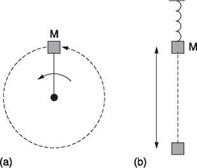
Figure 2.20(a) shows a steady rotation which could be a mass tethered by a string. Tension in the string causes an inward force that accelerates the mass into a circular path. The tension can be described as a rotating vector. When viewed from the side, the displacement about the vertical axis appears sinusoidal. The vertical component of the tension is also sinusoidal, and out of phase with the displacement. As the two parameters have the same waveform, they must be proportional. In other words the restoring force acting on the mass is proportional to the displacement.

Fig. 2.20 (a) A tethered mass is moving in a circle. If the component of this motion in one axis only is resolved, the motion will be found to be the same as a mass supported on a spring, (b).

Figure 2.20(b) shows that the same characteristic is obtained if the mass is supported on a spring. The mass supported by a spring is found widely in engineering because structures have mass and can never be infinitely rigid. An ideal spring produces a restor­ing force proportional to the displacement. The constant of proportionality is called the stiffness and is the reciprocal of compliance. When such a system is displaced there is sustained resonance. Not surprisingly the displacement is sinusoidal and is called simple harmonic motion or SHM and has all of the characteristics of one dimension of a rotation as shown in Figure 2.17.

The only difference between the mass on a string and the mass on a spring is that when more energy is put into the system, the mass on a string goes faster because the displacement cannot increase but more tension can be produced. The mass on the spring oscillates at the same frequency but the amplitude has to increase so that the restoring force can be greater.

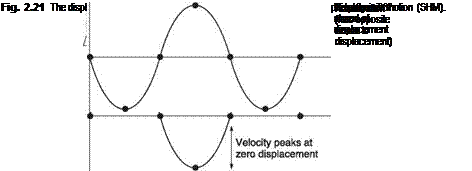The velocity of a moving component is often more important than the displacement. The vertical component of velocity is obtained by differentiating the displacement. As the displacement is a sine wave, the velocity will be a cosine wave whose ampli­tude is proportional to frequency. In other words the displacement and velocity are in quadrature with the velocity lagging. This is consistent with the velocity reach­ing a minimum as the displacement reaches a maximum and vice versa. Figure 2.21

shows the displacement, velocity and acceleration waveforms of a body executing SHM (simple harmonic motion). Note that the acceleration and the displacement are always anti-phase.

Eventually the resonance of a mass on a spring dies away. The faster energy is taken out of the system, the greater the rate of decay. Any mechanism that removes energy from a resonant system is called damping.

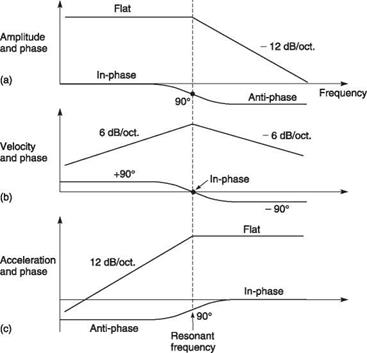
The motion of a rigid body can be completely determined by the mass, the stiffness and the damping factor. It is important to consider what happens when resonant systems are excited at different frequencies. Figure 2.22 shows the velocity and dis­placement of a mass-stiffness-damping system excited by a sinusoidal force of constant amplitude acting on the mass at various frequencies. Below resonance, the frequency of excitation is low and little force is needed to accelerate the mass. The force needed to deflect the spring is greater and so the system is said to be stiffness controlled. The amplitude is independent of frequency, described as constant amplitude operation, and so the velocity rises proportionally to frequency below resonance.

Above resonance the inertia of the mass is greater than the stiffness of the spring and the response of the system is described as mass controlled. With a constant force there is constant acceleration yet as frequency rises there is less time for the acceleration to act. Thus velocity is inversely proportional to frequency. As the displacement is the integral of the velocity the displacement curve is tilted by an amount proportional to frequency so that below resonance the displacement is constant and in-phase with the

Stiffness Damping Mass control control control Fig. 2.22 The behaviour of a mass-stiffness-damping system: (a) amplitude, (b) velocity, (c) acceleration

force whereas above it is inversely proportional to the square of the frequency and is anti-phase to the force.

In the vicinity of resonance the amplitude is a function of the damping and is said to be resistance controlled. With no damping the Q-factor is high and the amplitude at resonance tends to infinity, resulting in a sharp peak in the response. Increasing the damping lowers and broadens the peak so that with high damping the velocity is nearly independent of frequency. Figure 2.23 shows the effect of different damping factors on the step response, i. e. the response to a sudden shock. The underdamped system enters a decaying oscillation. The overdamped system takes a considerable time to return to rest. The critically damped system returns to rest in the shortest time possible subject to not overshooting.

Below resonance the displacement of the spring is proportional to the force. Here force and displacement are in phase. Above resonance the acceleration of the mass is proportional to the force. Here force and acceleration are in phase. It will be seen from Figure 2.22 that the velocity leads the displacement but lags the acceleration. Consequently below resonance the velocity leads the applied force whereas above reson­ance it lags. Around resonance there is a phase reversal so that at the precise resonant frequency there is no phase shift at all. Figure 2.24 shows that the rate of phase change in the vicinity of resonance is a function of the damping.

It will be clear that the behaviour just noted has a direct parallel in the behaviour of an electronic damped tuned circuit consisting of an inductor, a capacitor and a resistor and the mathematics of both are one and the same. This is more than just a convenience because it means that an unwanted mechanical resonance or phase change in a control system can be suppressed by incorporating at some point a suitable electronic circuit designed to have the opposite characteristic. Additionally by converting mechanical parameters into electrical parameters the behaviour of a mechanism can be analysed as if it were an electronic circuit.

It was seen in Figure 2.17 that a sinusoidal function is a rotation resolved in one axis. In order to obtain a purely sinusoidal motion, the motion on the other axis must be eliminated. Conceptually this may be achieved by having a contra-rotating system in which there is one rotation at +rn and another at —rn. Figure 2.25(a) shows that the sine components of these two rotations will be in the same phase and will add, whereas

©-©- -©/©

і і

the cosine components will be in anti-phase and will cancel. Thus all real frequencies actually contain equal amounts of positive and negative frequencies. These cannot be distinguished unless a modulation process takes place. Figure 2.25(b) shows that when two signals of frequency ±&>1 and ±&>2, are multiplied together, the result is that the rotations of each must be added. The result is four frequencies, ±(ш1 + ю2) and ±(ш1 — rn2), one of which is the sum of the input frequencies and one of which is the difference between them. These are called sidebands. Sidebands are found extensively in avionics, where the deliberate use of the process is called heterodyning. In a communications radio the carrier frequency is multiplied or ‘modulated’ by the audio speech signal, called the baseband signal, and the result is a pair of sidebands above and below the carrier.

The rotation of the helicopter rotor has a certain frequency. Any vibration due to periodic motion affecting the movement of the blades within the rotor plane may have a characteristic frequency with respect to the rotor. When referred to the hull of the helicopter, the frequency of the vibration may have been heterodyned by the rotor frequency and the frequencies experienced in the hull may then be the frequencies of the sidebands. This will be considered in Chapters 3 and 4.

In a voice radio system, the carrier frequency is much higher than the frequencies in the speech, whereas in other systems this may not be the case. In digital systems, contin­uous signals are represented by periodic measurements, or samples, and sidebands are found above and below the frequency of the sampling clock Fs. Figure 2.26(a) shows the spectrum of a sampling clock which contains harmonics because it is a pulse train not a sinusoid. Figure 2.26(b) shows that the sidebands of the sampling frequency can be rejected using a low-pass filter which allows through only the original baseband signal. The sampled representation of the signal is returned to a continuous waveform. This is exactly what happens in a Compact Disc player.

As the baseband frequency rises, the lower sideband frequency must fall. However, this can only continue until the base bandwidth is half the sampling rate. This is known as the Nyquist frequency and it represents the highest baseband frequency at which the original signal can be recovered by a low-pass filter.

(a)

(c)

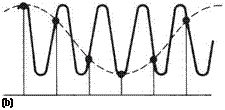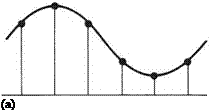
Fig. 2 .27 In (a) the sampling is adequate to reconstruct the original signal. In (b) the sampling rate is inadequate, and reconstruction produces the wrong waveform (dashed). Aliasing has taken place.

Figure 2.26(c) shows what happens if the base bandwidth increases beyond the Nyquist frequency. The lower sideband now overlaps the baseband signal. As a result, the output frequency appears to fall as the input frequency rises. This is the phenomenon of aliasing. Figure 2.27 shows aliasing in the time domain. The waveform carried in the envelope of the samples is not the original, but has a lower frequency. There is an interesting result when the two frequencies are identical. The lower side­band frequency becomes zero. This forms the basis of Fourier analysis seen in the next section. It is also exactly what happens when a stroboscope is used, perhaps to check the tracking of a helicopter rotor. The frequency of the flashing light (the sampling rate) is adjusted until it is the same as the rotational frequency of the object to be studied. The lower sideband frequency becomes zero and the object appears stationary. The upper sideband frequency is usually visible as flicker.

Small variations in the frequency of the strobe light above and below the rotational frequency will cause the rotating object to turn slowly forwards or backwards. The for­ward rotation is due to the lower sideband having a low frequency. However, when the strobe frequency is above the rotational frequency, the lower sideband frequency becomes negative, hence the illusion of reversed rotation. On a spectrum analyser, the negative frequency would fold about zero Hz to become a positive frequency. This fold­ing phenomenon is particularly important to an understanding of ground resonance that will be considered in Chapter 4.

Fourier was a French mathematician who discovered that all periodic or repetitive phenomena, however complex, could be described as the sum of a number of sinusoidal phenomena. As the rotation of a helicopter rotor is periodic, then Fourier analysis is a useful tool to study rotor motion.

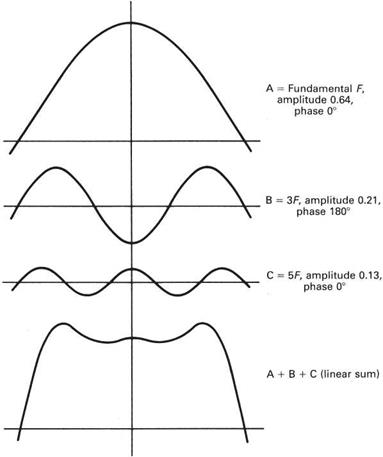
It was shown above that the sine wave is the waveform of a single frequency. Musically such a waveform would be called a pure tone or fundamental and the frequency would determine the pitch. If musical instruments only produced pure tones they would be hard to tell apart. They sound different partly because of the presence of harmonics. Harmonics are frequencies given by multiplying the frequency of the fundamental by a series of whole numbers. Figure 2.28 shows the waveforms of such harmonics. The final waveform is the sum of all of the harmonics. The relative amplitude of the different harmonics determines the tonality or timbre of an instrument. What Fourier did was to show how to measure the amplitude of each harmonic in any periodic waveform. The mathematical process that does this is called a transform. Reversing the process

Fig. 2.28 Fourier analysis allows the synthesis of any waveform by the addition of discrete frequencies of appropriate amplitude and phase.

by creating all of the right harmonics and adding them is called an inverse transform. Figure 2.29 shows how a square wave can be synthesized in this way by adding together different harmonics of the correct amplitude and phase.

Fourier analysis is based on multiplying the waveform to be analysed by sine waves called ‘basis functions’. In order to analyse an arbitrary waveform to see if it contains a particular frequency, it is multiplied by a basis function at that frequency and the product is averaged. Figure 2.30(a) shows that if the signal being analysed contains a component having the same frequency as that of the basis function the product will have a zero frequency component that will give a finite result after averaging. The value of the result after averaging is called a coefficient. Components at all other frequencies will average to zero. Thus a complete Fourier analysis requires the process to be repeated at all of the frequencies of interest.

Figure 2.30(c) shows that if by chance the input and the basis function have a phase difference of 90° the product will be zero even though the frequencies are identical.

Fig. 2.29 Fourier analysis of a square wave into fundamental and harmonics. a, amplitude; S, phase of fundamental wave in degrees; 1, first harmonic (fundamental); 2 odd harmonics 3-15; 3, sum of harmonics 1-15; 4, ideal square wave.

To overcome this problem the Fourier analysis searches for each frequency using both a sine wave and a cosine wave basis function. Thus at each frequency two coefficients will be obtained. The ratio of the two coefficients can be used to determine the phase of the frequency component concerned.

The full frequency accuracy of the Fourier transform is only obtained if the averaging process is performed over a very long, ideally infinite, time. In practice this may cause difficulties, not least with the amount of computation required, and the averaging time may need to be reduced. If a short-term average is used, the same result will be obtained whether the frequency is zero or very low, because a low frequency doesn’t change very much during the averaging process. Thus the short-term Fourier transform (STFT) allows quicker analysis at the expense of frequency accuracy. For best frequency accuracy, the signal has to be analysed for a long time and so the exact time at which a particular event occurs would be lost. On the other hand if the time when an event occurs has to be known, the analysis must be over a short time only and so the frequency analysis will be poor. In the language of transforms, this is known as the Heisenberg inequality. Werner Heisenberg explained the wave-particle duality of light. When light is analysed over a short time, its frequency cannot be known, but its location can. Light can then be regarded as a particle called a photon. When light is analysed over a long time its frequency can be established but its location is then unknown and so it is regarded as a wave motion.

In helicopters the frequencies of interest will generally be known from the rotor speed and usually only the first few harmonics contribute to the aerodynamic result although higher harmonics may result in vibration. These harmonics are normally sufficiently far apart in frequency that the time span of the analysis is not critical.

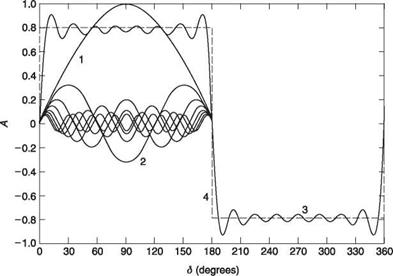
One peculiarity arises with Fourier analysis of helicopter rotors. The behaviour of a typical rotor is such that the coefficients of the harmonics are always negative.

Fig. 2.30 The input waveform is multiplied by the target frequency and the result is averaged or integrated. At (a) the target frequency is present and a large integral results. With another input frequency the integral is zero as at (b). The correct frequency will also result in a zero integral shown at (c) if it is at 90° to the phase of the search frequency. This is overcome by making two searches in quadrature.

For simplicity the traditional practice has been to redefine the transform so that the numbers come out positive. This causes confusion for those who are familiar with transforms but are studying helicopters for the first time.

Most calculations in mechanics involve a stationary frame of reference. However, as helicopters contain some major rotating parts, designers sometimes find it convenient for analysis to use a rotating frame of reference turning at the same angular velocity as the blade. The blade is then usefully more or less stationary with respect to the

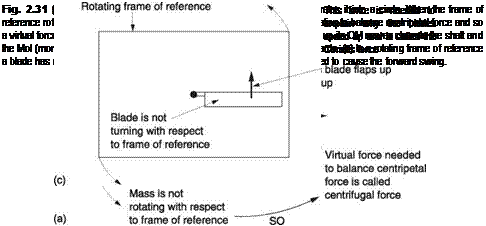frame of reference. Figure 2.31(a) shows that when the frame of reference rotates at the same angular velocity as the component of interest, the rotation disappears and so that component cannot be accelerating due to the rotation. However, the centripetal force due to the rotation is still acting and in order to maintain equilibrium with the

centripetal force in the absence of acceleration, a new virtual force of equal magnitude but opposite direction has to be imagined to act. This is called the centrifugal force. In the real world centrifugal force does not exist, it is a mathematical convenience needed to allow an apparent state of equilibrium in a rotating frame of reference.

In a fixed frame of reference, consider a turning rotor. Figure 2.31(b) shows that if one of the blades should move upwards, the centre of mass of the blade will move closer to the axis of rotation, reducing the moment of inertia. Conservation of momentum requires that the reduced moment of inertia be balanced by an increase in velocity. Consequently the blade will accelerate in the direction of rotation as it moves up. Naval gunners discovered a related effect which is that when a shell is fired a distance of several miles, the shell moves significantly with respect to the earth’s axis in a rotating frame of reference and so it will also experience conservation of momentum which takes it to the left or right of its intended target. These are examples of the Coriolis effect, named after the mathematician who derived the mechanics of rotating frames of reference.

Figure 2.31(c) shows that when the frame of reference rotates at the same angular velocity as the component of interest, the rotation apparently disappears. However, the conservation of momentum effect is still occurring and the blade appears to accelerate with respect to the frame of reference. In order to account for this acceleration, a new virtual force is imagined to act. This is called the Coriolis force. In the real world the Coriolis force does not exist, like centrifugal force, it is a mathematical convenience needed to allow the use of a rotating frame of reference.

The uninformed will often make reference to both centrifugal and Coriolis forces as though they really existed, usually as a result of reading an advanced textbook without understanding it. Such observations must be treated with suspicion. Centrifugal force and Coriolis force are the technical equivalent of the unicorn and the mermaid. They are in the imagination and the literature but they don’t exist.

There is a further consequence of the use of a rotating frame of reference that affects vibration frequencies created in the rotor and transmitted to the hull. The frequencies generated in the rotor may have the rotational frequency of the rotor both added and subtracted. The phenomenon is known as heterodyning and was treated in section 2.11.

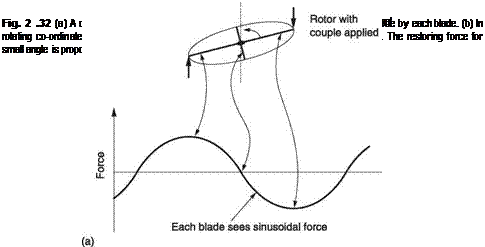
The rotors of a helicopter at flight RPM contain a large amount of stored energy and this alters the way they respond to forces. In order to control the helicopter, the entire rotor has to be tilted in the direction the pilot wishes to go. This will not be achieved by applying a couple in that direction. Figure 2.32(a) shows that if one blade is considered, when a couple is applied to the rotor, as it rotates the couple will alternately try to move the blade up and down. In fact in a rotating frame of reference the blade experiences a sinusoidal forcing function at the rotational frequency of the rotor. The way in which the blade responds to this is non-intuitive.

Figure 2.32(b) is drawn in a rotating frame of reference with respect to which the blade is stationary and it becomes correct to refer to centrifugal force. The figure shows that if it is assumed that the blade is displaced from its normal plane of rotation and released, there will be a component of centrifugal force trying to return the blade to the original plane. For small angles this force is proportional to the displacement, so the condition for SHM is met. The blade will oscillate like a pendulum about the normal plane at some natural frequency. This frequency can be calculated from the mass of the blade and the centrifugal force. It turns out that the frequency is nearly identical to the rotational frequency.

(b)

As a result when an external couple tries to tilt the plane of a rotor, the sinusoidal force on each blade is driving the blade at its natural resonant frequency. Section 2.9 showed that at resonance the driving force is in phase with the velocity. This means (from Figure 2.22) that the displacement lags both the velocity and the force by 90° of rotation. Thus the rotor does not tilt in the direction of the applied couple, but on an axis that is 90° further around the rotor in the direction of rotation. This is a fundamental characteristic of gyroscopes and is called gyroscopic precession (invariably changed to procession by the ill-advised use of spelling checkers). This 90° lag in the response of a rotor to applied forces has a significant bearing both on the control of the helicopter and on how it responds to external forces. The controls have to be connected up at right angles to the intuitive way.

As the blade tension is proportional to the square of RRPM (rotor revolutions per minute), when the rotors are turning slowly, the acceleration experienced by the blades due to rotation is small and the phase lag due to precession will be considerably reduced. The helicopter cannot fly at such low RRPM, but the effect may be noticed during rotor start or shutdown in a strong wind. When the pilot tries to minimize blade sailing by using the cyclic control, it will be found that the response is not as expected. Instead at low speeds the blades will respond with an advance with respect to the cyclic control. On a clockwise-from-the-top helicopter if the blades sail up on the right, the cyclic stick will have to be moved backwards.

When bodies move in a straight line, all of the body is going at the same velocity and energy calculations are easy. However, when a body rotates, those parts furthest from the axis are going faster than those parts near the axis. The amount of rotational energy stored is a function of the distribution of mass with respect to the axis of rotation. This is measured by the moment of inertia (MoI). In a flywheel, as much mass as possible is concentrated at the outside of the rotor to give the greatest MoI.

Angular momentum is the product of inertia and the rate of rotation about a given axis. Earlier in this chapter it was seen that a body may be accelerated by changing its speed or its direction. The same is true of a gyroscope. Changing rotational speed is acceleration but so also is changing the direction of the rotational axis. If the rotor is spinning rapidly it has a large momentum, and even a very small rate of movement of the rotational axis represents a large rate of change of momentum and so a large force is necessary. Put simply a gyroscope tends to resist disturbances to its axis in a manner disproportionate to its weight. That makes it attractive for aviation where weight is at a premium. The tendency to resist axis disturbance is called rigidity.

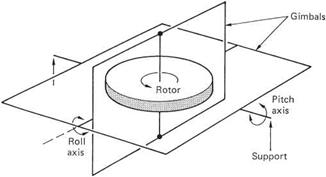
Figure 2.33(a) shows a gyroscope suspended by the shaft in a pair of nested cages called gimbals. The axis of rotation is vertical and the gimbals allow turning in two

(a)

(b)

orthogonal (at 90° to one another) horizontal axes. If the base of the system is pitched and rolled, the rigidity of the gyroscope will be much greater than the friction in the gimbals and the result is that the gyroscope axis remains vertical so that its angular momentum stays the same. Figure 2.33(b) shows that a couple is being applied to the outer gimbal, which tries to twist it in the direction shown. The couple is transmitted through the bearings of the inner gimbal and to the rotor shaft. If a small element on the periphery of the flywheel is considered, this reacts in the same way as the blade in the previous section. As the flywheel is really a collection of such elements, all of which behave in the same way, it is clear that in response to a couple on the outer gimbal axis, the rotor responds by turning around the inner gimbal axis.

The gyroscope rotor has a 90° phase lag just like a helicopter rotor. The outer gimbal will not turn because the applied couple is perfectly opposed by a reaction due to the rigidity of the gyro. The gyro can only generate the rigidity reaction by changing its angular momentum and to do this it must precess as the rotational speed cannot change. The rate of precession is proportional to the applied couple and inversely proportional to the angular momentum.

The mechanical gyroscope held sway for a long time but has recently been supplanted by two alternatives. A piezo-electric material is one that deflects when an electrical voltage is applied to it and which creates an electrical voltage when it is distorted. The quartz crystal in an electronic wristwatch works on the same principle. In the quartz watch the natural mechanical resonant frequency of the crystal forms the timing reference. Signals from sensing electrodes measure the deflection and are amplified and fed to drive electrodes that cause the crystal to resonate. By dividing down this highly stable frequency a count of seconds can be obtained.

In the piezo-electric gyroscope a vibrating element is made to oscillate as shown in Figure 2.34(a). If the assembly then rotates, the Coriolis effect causes a component

of oscillation to occur at right angles to the main oscillation. Further electrodes and suitable electronic circuits can measure the amplitude and sense of the Coriolis effect that is proportional to the angular velocity.

A piezo-electric gyroscope may be only 20 mm long and weighs a few grams. The power consumed is a few milliWatts. They were initially developed for image stabiliz­ers in consumer video camcorders. These gyros have already eclipsed the mechanical gyro in model helicopters on account of the low power and weight, and may find cer­tain applications in full-size machines in due course. The small size allows completely redundant units where two or more sensors can be used in case one fails.

In the laser gyroscope, shown in Figure 2.34(b), light from a laser is split into two components and sent in both directions round an optical path. As the distance in both directions is the same, the two components will emerge in the same phase. However, if the optical path rotates about the axis shown, light travelling in one direction will take a slightly longer time and that travelling in the other direction will take a shorter time. The two components will no longer be in phase and the phase difference is proportional to the angular velocity. This can be sensed electronically. These alternative gyros both have the advantage of freedom from wear.

Control signalling conveys the desired position of a flight control or a subsidiary con­trol from one part of the airframe to another. The next essential is to ensure that when a command is received it is carried out accurately. Feedback is a useful tool to reach this goal. Feedback is a process that compares the current condition of a system with a desired condition and tries to make that difference smaller. This is exactly the charac­teristic needed to make a remote load follow a control signal, hence the extensive use of feedback in control systems. Feedback may be implemented in mechanical, hydraulic and electrical systems and in the case of the latter may be implemented with analog or digital techniques, although the principles remain the same in each case.

Figure 2.35(a) shows a basic electrical feedback servo system. The desired position of the load is defined by setting a control potentiometer that creates a proportional electrical voltage. The actualposition of the load is measured by a second potentiometer. The actual position voltage is subtracted from the desired position voltage to create a signal called the position error. This is a bipolar signal whose polarity indicates the sense of the error and whose magnitude indicates how far the load is from the desired position.

The position error is amplified and, in this example, used to power a DC electric motor that drives the load and the feedback potentiometer. The polarity of the system must be such that the motor runs in a direction to cancel the position error. In other words the system has negative feedback: the information regarding the position of the load flows to the error sensor and the error information flows to the load forming a closed loop or feedback loop.

If the control potentiometer is set to a new position, a position error will result which will drive the motor until the error becomes zero again. The power to the motor will then be zero. In most cases this will not cause the motor to stop. The motor and the load have inertia and once in motion may continue even if the motor power is removed. As a result the load may overshoot the desired position. This will cause a reverse position error so the motor is driven back. Again the load may overshoot and an indefinite or decaying oscillation known as hunting takes place.

This is not acceptable in any precision system. The problem of hunting is due to considering only the position of the load. The solution is to consider the load’s velocity as well. In this way the control system knows how much kinetic energy is stored in the moving load so that it can be brought to rest by applying a suitable reverse drive. Figure 2.35(b) shows that in this example the load velocity can be measured with a tachogenerator connected to the motor shaft. Many servo motors are designed with an integral tachometer.

If the control potentiometer is set to a new position, the position error will drive the motor to cancel the error. As the load gathers speed, the load velocity signal will be subtracted from the position error. As the load approaches the desired position, the position error becomes smaller, and when the position error is less than the velocity, the signal driving the motor will actually reverse polarity so that the load is retarded. This retardation process damps the hunting tendency. Instead of having a separate tachometer the velocity of the load can be obtained by differentiating the actual position signal.

The performance of a servo may be tested by measurement of the response to a step input. The speed of response can never exceed the limits set by the motor power and
the inertia of the system that determine the maximum slew rate. Figure 2.23 showed the effect of different damping factors on system response. In the case of a servo the amount of velocity feedback determines the damping factor. With little or no velocity feedback the slew rate will be high, but hunting will be excessive and the step response will be a decaying oscillation. With too much velocity feedback the response will have no overshoot, but will be very slow. In between these is the condition known as critical damping. This is defined as the amount of damping which gives the fastest response without any overshoot. The critical damping condition is simply a definable condition, and it is not necessarily the optimum response. In most cases the response speed can be increased significantly with the penalty of a very small overshoot.

In an unpowered system, if the pilot experiences resistance to a control input, he will automatically apply more force to obtain the desired control position. In a fully powered system, the pilot (or the autopilot) does not feel this resistance and cannot compensate. The feedback system must be designed to overcome resistance automatically. In a simple servo, the load will stop at a position where the force from the motor is balancing the disturbing force. Clearly in a simple feedback system, the motor can only produce a force if there is a position error. The result is that the external force pushes the load out of position until the position error is large enough to oppose further motion. The ability of a servo to oppose external force in this way is called stiffness.

The stiffness of a servo can be improved by increasing the gain given to the position error. Then a given resistance to an external force will be obtained with a smaller posi­tion error. Increasing the gain may also speed up the step response, but not beyond the slew rate limit. If a control input exceeds the slew rate limit, for a period of time the position error will be large and the system is not feedback controlled. In this state the system is said to be in an open loop condition.

Clearly high gain is desirable in a servo because it increases response speed and stiffness. However, high gain can also cause instability. During servo development, a control input is created which is sinusoidal and the frequency is swept upwards from a very low value. The amplitude and phase response are plotted against the frequency. As the frequency rises, the servo has to work harder to follow the rapid movement and so the position error may increase. This causes the load to lag the input. At some high frequency, the phase lag may reach 180°.

With a 180° phase shift, a negative feedback system has turned into a positive feed­back system. In other words the sense of the correcting action is wrong. If the loop gain is above unity at the frequency where the phase response has gone to 180°, the system will oscillate at that frequency. This may be spontaneous upon applying power or result from a small control input. Clearly this would be catastrophic in any control system. In practice feedback systems must contain a filter to reduce the loop gain at high frequencies to prevent oscillation.

Another possibility that allows higher loop gain is to have a signal processor con­taining an inverse model of the phase characteristics of the servo loop. When the servo loop lags, the processor will introduce a phase lead to balance out the lag. The use of these filters and processors in a servo loop is called compensation.

If high gain cannot be used for stability reasons, it is possible to improve the accuracy of a servo in the long term by integrating the error. Figure 2.36 shows a feedback system with integral control. A small error at the input to the integrator will become larger as the integrator operates until the loop acts to cancel it. Integral control is useful for overcoming friction in mechanisms.

Feedback loops can be nested which means that one operates inside another. For example, Figure 2.37 shows an automatic navigation system. The flight director error loop provides an error signal to the autopilot in order to keep the machine on track.

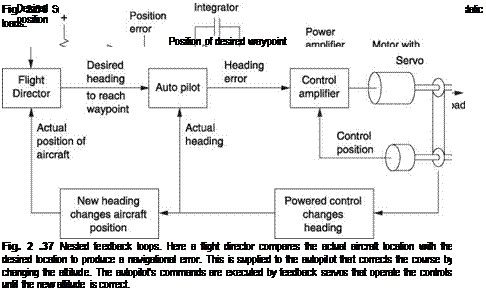The autopilot loop responds by producing an attitude error that keeps the machine in the attitude needed to hold the new track. The attitude error is supplied to the powered control system loop that actually controls the rotors.

The advantage of nested feedback is that each loop is stabilized in its own domain. The powered control loop is compensated to prevent oscillation or instability in the rotor systems, the autopilot loop is compensated to prevent instability in the attitude of the machine and the navigation loop is compensated to prevent the machine following a serpentine track to the waypoint. A further advantage of the nested loop is that different parts can be changed. An inertial navigator could be replaced with a GPS navigator, for example. Also in the case of a failure, only the affected loop needs to be
shut down and replaced by pilot action. For example if the autopilot failed, the pilot could still use the outputs of the navigator and the power assistance, but he would have to move the controls to stabilize the attitude of the machine on the course stipulated by the flight director.

Feedback loops have many advantages, but they do behave badly in the event of certain failures. If the position feedback sensor of Figure 2.35 failed or jammed, the movement of the load would not reduce the servo error and the servo would inadver­tently keep driving the load in the direction that would normally reduce the error, until the load reached a mechanical limit or stop. This is a characteristic of feedback loops, which is that when they fail they generally go to one control limit. This is known as a hardover.

Helicopters have crashed because a stability augmentation system had a hardover failure. Subsequently systems were designed with limited authority so that even if a hardover occurred, the amount of incorrect control travel or the force produced was not so great that the pilot could not overcome it. The end stops of the servo could be brought closer to the neutral position and a slipping clutch could be fitted in the drive train. Today part of the certification process is to prove that the pilot can overpower the servo so that control can be retained if a stability augmentation system has a hardover failure. If this is impossible, the system will have to be made failsafe by incorporating redundancy.

Certain helicopters use a redundant system in which the autopilot or stability aug­mentation signals are generated in two independent systems and fed to two motorized servos that drive the controls through a differential gear. In the event that one of the servos experiences a hardover failure, the tachometer of the failing system will output an unusually large signal. Detection of the hardover condition will shut down the fail­ing servo by removing power and apply a shaft brake to lock the motor. The remaining servo will be able to retain control through the differential gear and the performance will be identical if the signal which shuts down the failing servo also doubles the travel of the surviving servo.

In a fully powered feedback servo system, the pilot simply moves a transducer and the feedback loop will do whatever it can to carry out the command. It will still try even if enormous resistance is met. This may result in overstressing and a solution is a system of force feedback. The control stick is not centred by a spring, but by a force motor. The resistance felt by the pilot comes from the force motor that produces a force proportional to the force being exerted by the servo. In this way the pilot produces a small force that is used to control the machine, but he also experiences a scaled down replica of the resistance to the control efforts.

This gives the pilot a good sense of how much stress the machine is under. Force feedback systems of this kind are also known as artificial feel systems. Artificial feel of this kind can also be used with autopilots. If an altitude error is suddenly experienced due to turbulence, the autopilot could react very quickly and powerfully, but to do so would stress the airframe and cause discomfort to the passengers. It may be better to take longer to cancel the error by reacting more gradually.

Feedback is used in servos designed for radio control of models. These work on the principle of pulse width modulation where the length of a pulse, typically 1 millisecond at the neutral position, is increased or reduced as a means of control signalling. A servo operating on pulse width signalling can use feedback based on comparison of pulses. The feedback potentiometer controls a pulse generator and the servo error is obtained by determining the difference in pulse width between the input and the feedback pulses. The error pulses are used directly to drive the motor amplifier. As the error becomes smaller, so does the width of the pulses, reducing the drive to the motor. Velocity may be sensed by measurement of motor back EMF whilst the amplifier is switched off. Pulsed amplifiers are electrically efficient because they are either on or off and so dissipate little heat. This is important in models where the power source will be a battery.

Although this section has considered a simple feedback system in which the controls are signalled by analog voltages or variation of pulse width, it is possible to build feedback systems using any type of signalling or even a mixture of types. Chapter 7 considers various methods including digital signalling.

 

This chapter provides an introduction to concepts that will be needed to follow the technical explanations in the rest of the book.

 

2.1 Introduction to mechanics

 

Mechanics is the study of how objects interact with the forces applied to them. Designers are concerned with resisting the forces generated in flight so that the machine stays intact. Using the controls of a helicopter the pilot changes the forces applied to it and thereby determines the path it takes. It is important for a pilot to understand some mechanics so that he can predict what control movements will be necessary to make the machine do what is wanted. When this happens, the pilot is said to be in control. Any other situation is not recommended.

 

2.2 Mass and density

 

The amount of matter in a body is specified by its mass, measured in pounds (lb) or kilograms (kg). Since the amount of matter in a body cannot readily change, the mass is the same wherever the body is and however it moves. The density of a substance is the mass of unit volume. In the old imperial units, density was expressed as pounds per cubic foot. In the SI system, the term ‘relative density’ is used, where water has a relative density of one.

 

Although helicopters must all follow the same laws of physics, the forms that practical machines take vary tremendously due to the range of tasks to which they can be put. To avoid confusion, this book takes the view that an aircraft is any man-made aerial machine capable of climbing out of ground effect. Thus a helicopter must be an aircraft. Neglecting aerostats (balloons etc.) any aircraft that is not a helicopter will be an aeroplane (USA: airplane).

It will be seen later in this book that the slower an aircraft goes, the more power it needs to maintain height. Hovering is the ultimate case of slow flight, suggesting that helicopters must have a high power to weight ratio. This will require heavy engines and a corresponding fuel capacity. These factors limit load carrying capability and range.

The mechanical complexity of the helicopter and the inevitable vibration demand a lot of maintenance. The airspeed of the true helicopter is forever restricted by funda­mental limits. It will generally be more expensive to move a given load by helicopter than by almost any other means, and so if a suitable airstrip exists, a fixed-wing air­craft can do the job at lower cost, and generally at a higher airspeed. In most cases helicopters cannot compete economically with aeroplanes, and so their use is restricted to applications for which aeroplanes, or other forms of transport, are unsuitable.

In remote areas, there will be no airstrips; in wartime, runways are conspicuous targets, and, with the exception of the aircraft carrier, are fixed. The helicopter’s ability to hover means that it can land almost anywhere a fairly flat firm surface exists. Some are genuinely amphibious, landing with equal aplomb on water or land. If the ground is unsuitable (or if the waves are too high) many helicopters can transfer goods and passengers whilst in the hover.

This ability makes the helicopter the ideal rescue vehicle. Many lives have been saved because the helicopter can get to places that would otherwise be difficult or impossible to reach. War casualties, the victims of shipwrecks, mountain climbing accidents and natural disasters such as earthquake or flood today have significantly higher chances of survival because a helicopter can get them rapid treatment.

The accounts of helicopter rescues make more thrilling reading than novels because they are true. Helicopters have flown far out of range of the shore by taking fuel from oilrigs and ships, sometimes taking fuel in the hover if a landing was impossible. This would be remarkable in good weather, but emergencies occur in all weather conditions and the helicopter has evolved to handle the worst.

Despite their life-saving ability, most of today’s helicopters were originally designed for military use. As military fixed-wing aircraft became faster and faster, they found

it harder to attack ground targets or to support ground troops. During the Vietnam War, it was found that the helicopter had a major role. Transport helicopters excelled inserting and withdrawing troops, delivering ammunition and food, evacuating the wounded, recovering the crews of downed planes and even the planes themselves.

Armed helicopters proved to be ideal for attacking ground targets. At first these were general-purpose machines hurriedly fitted with weapons, but later dedicated attack helicopters evolved, complete with armour plating and redundant systems to allow them to withstand ground fire. As their load carrying capability has increased, these machines have virtually rendered the tank obsolete.

Although ideal against ground targets, the helicopter is slow and vulnerable to attack from the air. Fixed-wing planes are necessary to provide the air superiority in which the helicopters operate. As an alternative, helicopters can operate under stealth conditions, avoiding detection by using terrain.

Large military helicopters are very expensive to operate, and armed forces found it worthwhile to have simpler machines specifically for training purposes. A small number of helicopters have been designed specifically for the civil market and these are popular with large companies for executive transport.

For the average private owner, the sheer cost of running helicopters precludes all but the smallest machines with aeroplane-derived piston engines. Virtually all other helicopters are now turbine powered.

This is not a history book and this section must necessarily be brief. The reader inter­ested in the US history of the helicopter is recommended to the comprehensive yet highly readable works of Jay Spenser.1,2 The recent book by Steve Coates, Helicopters of the Third Reich,3 is essential reading to the historian as it shows how far ahead of the rest of the world German helicopter engineers were at that time. For those who read French, two more fascinating volumes are available. LHistoire de l’Helicoptere by Jean Boulet4 contains the words of helicopter pioneers themselves. Les Helicopteres Florine 1920-1950 by Alphonse DuMoulin5 recounts the pioneering work of Nicolas Florine.

The history of the helicopter has been very short indeed. In comparison with fixed – wing aircraft, helicopters need more power, have to withstand higher stresses, are harder to understand and control and have more moving parts. It is hardly surprising that the development of the helicopter took place well after that of the fixed-wing aircraft.

Early helicopters lacked enough power to fly. Once helicopters were powerful enough to leave the ground, they were found to be uncontrollable. Once the principles of control were understood, they were found to vibrate and to need a lot of maintenance and so on. Today’s helicopters represent the sum of a tremendous number of achievements in overcoming one obstacle after another.

Before World War II helicopters were in an experimental phase. This was the heyday of the gyroplane, invented by the Spaniard Juan de la Cierva and technically refined by Raoul Hafner, an Austrian working in England who would later contribute much to the development of the helicopter.6

The first practical helicopter was the Focke-Wulf Fw-61 of 1938 (Figure 1.1), followed in the same year by the Weir W-5 (Figure 1.2) that flew two years before Sikorsky’s VS-300 (Figure 1.3). The urgencies of war accelerated all technical development with the emergence of production helicopters, where the work of Anton Flettner (Figure 1.4) and Heinrich Focke was far in advance of anything taking place elsewhere.

Fig. 1.1 The Focke-Wulf Fw-61 was the first helicopter to move beyond the experimental stage and was capable of extended flights. The hull was based on that of an Fw Stieglitz aeroplane. Note the vestigial airscrew that simply cools the engine. (Steve Coates)

Fig. 1.2 The Weir W-5 flew extensively, but development of all helicopters was suspended in the UK during World War II. (AugustaWestland)

The Focke-Achgelis Fa-223 shown in Figure 1.5 became, on 6 September 1945, the first helicopter to cross the English Channel when a captured machine was flown to England by Hans Gerstenhauer. This machine had a payload of 2000 kg.7

Helicopter development in the UK was halted by government order during World War II and, being an Austrian, Hafner was locked up, but fortunately not for long.

Fig. 1.3 The Sikorsky VS-300 had an extended development period during most of which cyclic control was not understood and unwieldy auxiliary rotors were used instead. (Igor I. Sikorsky Historical Archives Inc.)

Fig. 1.4 The Flettner Kolibri (Hummingbird) was the first synchropter and was an advanced and capable machine. Kaman developed the concept and produced the successful Husky and K-Max models. (Steve Coates)

Fig. 1.5 The Focke-Achgelis Fa-223 was a large and capable machine that was in production during World War II. Few were produced due to Allied bombing. The machine was far ahead of anything else in the world at the time. (Steve Coates)

In Germany, production was hampered by Allied bombing, whereas US helicopters were unrefined. The result was the same: helicopters made little contribution to the war itself.

After World War II great progress was made in the understanding of helicopter dynamics and stability. This led directly to machines that were less stressful to fly and correspondingly safer. The Bell 47 (Figure 1.6) based on the research of Arthur Young was in 1946 the first helicopter to be certified. The Sycamore of 1952 (Figure 1.7) designed by Hafner, was the first British helicopter to be certified and was noted not just for its performance, but also for its light control forces which needed no power assistance.8

Advances in constructional techniques and materials continued to improve the service life of components, especially blades. Possibly the most significant single step

Fig. 1.6 The legendary Bell 47 was based on Arthur Young’s research and was the first helicopter to be certified in the USA. Larry Bell never liked the utilitarian appearance, but it outsold all of the more stylish models. The flybar stabilization system was adopted extensively in later Bell machines. (Bell Helicopter Textron)

Fig. 1.7 The attractive Sycamore was Hafner’s masterpiece and the first helicopter to be certified in the UK. (AugustaWestland)

Fig. 1.8 The Bell Huey was officially designated the Iroquois, but the Helicopter, Utility designation, HU-1, led to the nickname of Huey, which stuck. In Vietnam the Huey was used in enormous numbers. (Bell Helicopter Textron)

was the introduction of the turbine engine which was much lighter than the piston engine for the same power, yet had fewer moving parts. This allowed greater payload and a reduction in maintenance.

The first turbine-powered helicopter to fly was a modified Kaman K-225 in 1951 and in 1954 the first twin-turbine machine, also a Kaman, flew. The Bell Huey first flew in 1956 (Figure 1.8). It was in the 1960s that the many disciplines in helicopter design were finally mastered allowing the machine to be considered as a system. Some elegant and definitive designs emerged during this period. Such was the validity of their basic concepts that they could accept a steady succession of upgrades that would allow them in some cases to remain in service to the present day. Sikorsky’s S-61 and Boeing’s Chinook are good examples of longevity.

Since that time there have been few breakthroughs; instead there has been a steady process of refinement. The introduction of composite materials in blades, rotor heads and body parts has reduced weight and extended service life. Refinements in mechani­cal engineering have produced lighter engines and transmissions having longer life. Manufacturers have used production engineering to reduce the amount of labour needed to build machines.

Instead of a revolution, the employment of electronics and computers in helicopters has seen steady and relentless progress. There is no wear mechanism in electronics and complicated transfer functions can be realized in lightweight parts that use little power. Items such as turbine engine controllers and rotor rpm governors are ideal applications for electronics, along with stability augmentation systems. The flexible control systems that electronics make possible have enabled developments such as the tilt-rotor helicopter.

Helicopters can survive engine failures and the failure of a variety of parts, but there remain some parts such as gearboxes and rotor heads in which failure will be catastrophic. The technique of electronically monitoring critical components has made a great contribution to safety. Spontaneous failures are very rare. Generally there are symptoms such as a change in the characteristic of vibration or noise. These may be too slight to be heard by the crew, but a sensor mounted on the affected part in conjunction with a signal processor which knows what the normal sounds, or signature, from the part are, can give vital warning of a potential problem.

The life of a component may be reduced if it is subjected to higher stress. Modern electronic systems (HUMS: Health and Usage Monitoring Systems) can measure stress and the time for which it has been applied in order to calculate the safe remaining life in major components.

Much fundamental research into helicopters was done using models. De la Cierva’s early work was with free flying model gyroplanes. Arthur Young used models exten­sively (Figure 1.9) and it was his demonstration of a model controlled by a trailing wire that convinced Larry Bell to enter the helicopter business. Irven Culver at Lock­heed built what was probably the world’s first radio-controlled model helicopter in the late 1950s.

Advances in radio control equipment in the 1960s made the necessary precision available at reasonable cost and this led to the availability of flying model helicopters

Fig. 1.9 Arthur Young flies a wire-controlled model helicopter. Young was a philosopher who argued that designing a helicopter would teach him how to think. He was right. (Bell Helicopter Textron)

for the model building enthusiast. As will be seen in Chapter 9, such models have become highly sophisticated even though, like their full-sized counterparts, they remain expensive to build and operate.

Conceptually somewhere between the model and the full-size helicopter is the UAV (unmanned autonomous vehicle). These machines are designed to perform surveillance tasks, typically carrying cameras and other sensors. As electronic and sensing devices have become smaller, useful equipment can be carried aloft at much lower cost if there is no need to carry a pilot. Unlike the model, which needs actively to be controlled by the pilot on the ground at all times, the UAV carries enough navigational equipment, automatic stabilization systems and processing power to be self-contained. Also unlike the hobbyist’s machines, UAVs must be built and operated to professional standards.

The definition of a rotorcraft is quite general, embracing any flying machine that produces lift from rotors turning in a plane that is normally close to the horizontal. This definition does not concern itself with the proportion of the machine’s weight carried by the rotors, or whether that proportion changes at different stages of flight. Figure 1.10 shows the main classes of rotorcraft that will be defined here.

The pure helicopter obtains the great majority of its lift in all modes of flight from a power driven rotor or rotors, and any lift due to airflow around the hull is incidental. The majority of today’s rotary wing machines are pure helicopters. The thrust from a rotor is closely aligned with a line drawn perpendicular to the tip path, and the pure helicopter propels itself by tilting the rotor forward to obtain a component of rotor thrust which balances the drag, as shown in Figure 1.10(a).

The gyroplane (also known by de la Cierva’s trade name of autogyro) obtains lift from an undriven rotor that must be tilted away from the direction of flight to make air flow up through it. The rearward rotor-thrust component, along with the drag, is balanced by the forward thrust of a conventional airscrew as shown in Figure 1.10(b). As the rotor needs to be pulled through the air to maintain height, the autogyro cannot hover in still air, although it can give the illusion of hovering by flying into wind. Simple autogyros must taxi to spin up the rotor, but later machines could spin the rotors with engine power on the ground, and use the stored energy to perform a jump take-off.

Between the pure helicopter and the gyroplane is the gyrodyne, which obtains lift from a power driven rotor. Unlike the pure helicopter, the gyrodyne maintains the rotor disc parallel to the direction of flight, as in Figure 1.10(c) and propels itself with a conventional airscrew. The Fairey Gyrodyne (Figure 1.11) replaced the tail rotor with a side-mounted airscrew to cancel torque reaction when hovering, but also to provide thrust for forward flight. More recently the Lockheed Cheyenne (Figure 1.12) had both anti-torque and pusher rotors at the tail. The gyrodyne offers high speed potential, with the penalties of raised complexity, weight and difficulty of control. Some gyrodynes have wings in addition to the rotor.

Fig. 1.11 The Fairey Gyrodyne had a side-mounted anti-torque rotor that became a tractor propeller in forward flight. (AugustaWestland)

Fig. 1.12 The Lockheed Cheyenne with fixed-wing, anti-torque rotor and pusher propeller was a very fast, highly manoeuvrable machine. (Lockheed Martin)

The compound helicopter is one that hovers like a helicopter, but which may obtain supplementary lift from fixed wings during flight and may incorporate additional means of providing forward thrust.

The convertiplane is a more extreme example of the compound helicopter in that it reconfigures its means of providing lift and propulsion in different flight regimes. The Fairey (later Westland) Rotodyne was a convertiplane. Figure 1.13 shows that it consisted of a twin turboprop aircraft-like structure with a pylon-mounted rotor driven by tip jets. As a helicopter, the tip jet drive provided lift, and yaw control was obtained by differentially changing the pitch of the turboprops. Forward thrust from the airscrews would bring the machine to cruising speed, where much of the lift was developed by the wing, and the tip jets were turned off such that the rotor free-wheeled and the machine became a compound gyroplane.

Reconfiguring can also be done by tilting the whole wing-engine-rotor assembly (tilt wing) as shown in Figure 1.14(a) or by tilting the engine-rotor units on fixed wings (tilt rotor) as in Figure 1.14(b). The Bell-Boeing Osprey is a tilt rotor. As can be seen in Figure 1.14(c), the diameter of convertiplane rotors is usually such that the machine cannot land in the forward flight configuration, but must return to the hover.

The advantages of the convertiplane over the pure helicopter are that using the rotors as airscrews reduces vibration, it is much more efficient and allows a higher airspeed. This reduces fuel consumed and allows greater range. The tilt rotor has its wing in the downwash which reduces hover performance, whereas in the tilt wing the wing is almost always working. However, the tilt wing needs a supplementary mechanism to control the pitch axis, such as a jet or rotor at the tail.

The various configurations of the pure helicopter will now be considered. The most common configuration is the single main rotor and the anti-torque tail rotor. The remaining configurations, shown in Figure 1.15, handle torque reaction by contra­rotation. Contra-rotating helicopters have no need for the tail rotor, but generally have a tail fin or fins for directional stability at speed.

In the tandem rotor helicopter, Figure 1.15(a), two rotors turn in opposite directions at the opposite ends of a long hull. The rotors are usually synchronized through a transmission system so that the shafts can be little more than a blade length apart. The Chinook in Figure 1.16 is a good example of the type, the large disc area offering good lifting ability, and the long cabin ample load space.

An alternative to the tandem rotor is the side-by-side twin rotor (Figure 1.15(b)). This has aerodynamic advantages in forward flight because the lifting area has a better aspect ratio, but it is difficult to avoid drag due to the structure needed to locate the rotors each side of the hull and to carry the transmission across the machine. See Figure 1.5. In large machines it is also difficult to make the structure stiff enough to avoid resonance and so the type is rare.

A relative of the side-by-side helicopter which has had more success is the synchropter (Figure 1.15(c)) in which the two rotors mesh so closely that the contra-rotating shafts can be driven by the same gearbox. The close meshing is achieved by tilting the shafts outwards so that the blades of one rotor can pass over the rotor head of the other. The German Kolibri of World War II, designed by Anton Flettner (Figure 1.4), was the first successful machine to use the idea. In the USA, Charles Kaman adopted the syn­chropter principle, and produced the famous H-43 Huskie which became the definitive crash rescue helicopter of its time (Figure 1.17). The synchropter is the easiest of all

Fig. 1.16 The Chinook is the definitive tandem rotor helicopter and has been produced in large numbers. (Boeing)

Fig. 1.17 The Kaman Huskie is the most successful synchropter design. Note the large fin area needed. (Kaman Aerospace)

helicopters to fly, as the interactions and second-order effects of the conventional configuration are eliminated, but replaced by some interesting yaw characteristics.

The final approach to contra-rotation is the coaxial helicopter. Stanley Hiller and Arthur Young both built such machines experimentally, but Nikolai Kamov in the USSR put the idea into production (Figure 1.18). The coaxial helicopter places both rotors one above the other on a common shaft, and drives them in opposite directions. Like the synchropter, control interactions are reduced, but yaw control remains an issue. The main advantage of synchropters and coaxial helicopters is that in the absence of a tail rotor, the machine can be much more compact, a crucial factor in naval aviation, where everything has to be squeezed into limited hangar space, although the height needed may increase. The alternative is to fit a folding tail on a conventional machine.

The helicopter contains a large number of systems and components, but these can generally be broken down into a smaller number of major areas. Figure 1.19 shows a cutaway drawing of a conventional tail rotor type helicopter. The main systems to consider in a helicopter are the hull or airframe, the engine and transmission, the fuel system, the landing gear, the rotors, the controls, electrical and hydraulic power,

instrumentation and avionics. These subjects will briefly be introduced in the remain­ing sections of this chapter, and references will be made to more detailed treatments elsewhere in the book.

The fuselage or hull has a number of jobs to perform. One obvious task is to hold all of the components in the correct position and to transfer forces from the rotors, the tail surfaces, the landing gear and any internal or underslung payload. It also protects the occupants and the mechanisms from the elements whilst still allowing good visibility for the pilot. Space has to be found for fuel tanks close to the centre of mass (CM) as single rotor machines are sensitive to trim shifts as fuel burns off. It will also have a more or less aerodynamic shape, although the other requirements often combine to prevent this. In some cases the hull will also be designed to float in case the machine is forced down over water, whereas in others, amphibious operation is planned.

Fuselage construction varies considerably, but the materials and techniques are not much different from those used in any aircraft. Early machines such as the Bell 47 were no more than a steel tube lattice frame with a blown acrylic canopy for the crew. Aerodynamic improvements came when the hull was faired in. The tail cone is often a stressed skin structure, but the centre section has too many doors, windows and access hatches for the skin to carry all the loads, and alloy frames or steel tubes are often used beneath the skin. The main landing gear often shares the same framework as the engine and transmission so that the skin is not unduly stressed on landing.

Figure 1.20 shows the structure of an Enstrom F-28. The landing skids, engine, fuel tanks and transmission are all attached to a welded tube frame known as a pylon. A stressed skin tail cone is attached to the rear of the pylon structure, and the aluminium seat and cabin floor is attached to the front. The cabin is glass fibre with plastics glazing. The cabin lines are faired into the tail cone by unstressed panelling attached to the pylon, so the machine has a sleek outline. Much of the unstressed centre panelling can be removed for servicing.

Composite materials are ideal for airframe construction and are becoming increas­ingly important since they are less dense than metals and are inherently well damped, which helps to control the inevitable vibration that characterizes helicopters. They can also have an indefinite fatigue life.

The engine or engines and transmission are generally close together. Piston engines are heavy, and they are almost always placed below the rotor head to balance the machine. Turbines are much smaller and lighter and are often built into the roof of the hull to maximize internal space. Both piston engines and turbines turn much faster than the rotor shaft, and the transmission must incorporate reduction gearing.

The gearbox will generate a good deal of heat on a large machine, and require an oil cooler. This will have its own air intake near the rotor shaft; often in the front of the pylon. The gearbox also drives the tail rotor shaft, which runs the length of the tail boom to the tail rotor gearbox. The tail rotor shaft is often mounted outside the tail cone for ease of inspection and maintenance.

The rotors may take some time to come to rest after the engines have been shut down, and this may be inconvenient. The civil user wants to disembark passengers with the rotors stopped. The naval user wants to put the machine on the elevator down to the hangar and the army user wants the rotors stopped quickly on a clandestine mission so that the machine can be camouflaged. This can be achieved by fitting a rotor brake on the transmission.

Helicopters have also been built with jets at the blade tips, and this has the advantages that no gearbox is required and there is no torque reaction. Unfortunately tip jets have short fatigue life, very high fuel consumption and noise level to match and are little used. They will not be considered further here.

As it is a major subject, the whole of Chapter 6 is devoted to helicopter engines and transmissions.

The fuel system can be simple or complex depending on the type of machine. In early piston engine machines using carburettors, the fuel system was little more than a pair of tanks that fed fuel by gravity through the pilot’s cut-off valve and a filter to the engine. The tanks in a gravity fed system are mounted one each side of the mast so that lateral and longitudinal trim is unaffected as fuel is consumed. The tanks are clearly visible on the Bell 47 and the Hughes 300. Larger machines will use the space below

the floor to put tanks close to the CM, in which case pumps will be required to feed the engines.

Piston engines burn AVGAS or aviation gasoline, which is basically similar to auto­mobile fuel but made to tighter quality standards. Turbines burn AVTUR that has a similar relationship to kerosene. As a piston engine will stop if AVTUR reaches it, pilots like to know they have taken on the right fuel. AVGAS fillers are marked red and AVTUR fillers are marked black to help prevent a dangerous mistake.

Recently there have been significant advances in the development of Diesel engines, allowing a similar power to weight ratio to a gasoline engine to be obtained. The advantage of the aeroDiesel is that it can burn AVTUR and its improved fuel economy allows better payload or range. A more detailed treatment of fuel systems can be found in Chapter 6.

The landing gear is subject to considerable variation. Utility and training helicopters are invariably fitted with skids to allow a landing on unprepared ground even with forward speed. Small wheels, known as ground handling wheels, can be fitted so the machine can be moved around. Some skids are broader than usual so they can act as skis for landing on snow or soft ground. Inflatable or rigid floats can be attached to the skids to permit operation over water, but there will be a drag and payload penalty. Larger machines invariably have wheels, as skids would make them too difficult to move. Naval helicopters need wheels to allow them to be moved below decks. In many cases the wheels can be locked so as to be tangential to a circle. The machine can be turned into the wind, but will not roll as the ship heels.

Landing gears often incorporate a telescopic section containing oil and a compressed gas acting as a spring. These are formally known as oleo-pneumatic struts, invariably abbreviated to oleos. When the length of the oleo changes, the oil is forced through a small orifice to damp the movement. The struts that hold up automobile tailgates work on the same principle, but these are sealed units whereas the type of oil and the gas pressure in an oleo may be adjusted to give the correct spring rate and damping.

One obvious purpose of the oleo is to absorb the impact of landing, but a more important role is to control ground resonance. Ideally the rotor blades rotate with perfectly even spacing when run up on the ground, but it is possible for them to be disturbed from that condition. This results in the CM of the rotor moving away from the shaft axis and the rotor tries to whirl the top of the hull in a circular orbit. Under certain conditions this motion becomes uncontrollable unless there is damping to dis­sipate the energy. The origin of ground resonance will be discussed in Chapter 4 where it will be shown that the rotor head may also need dampers to prevent the problem.

The main rotor takes the place of the wings of a conventional aircraft, and it is not unrealistic to think of a helicopter as being supported by the lift from wings that rotate instead of flying in a straight line. The main difference between rotor blades and

wings is that the former are in comparison very thin and flexible, and the forces acting upon them are greater and more rapidly varying. The rotors have more to do than an aeroplane wing, because they are also the control system. Chapter 3 explains how the rotors produce lift and introduces the control of the machine.

The control system cannot be treated in isolation, but must be integrated into the design of a machine from the outset. In the pure helicopter, control of the machine is achieved entirely by changing the pitch of the main and tail rotor blades in various ways. This will then determine the amount of engine power needed. The rotors are generally designed to turn at constant speed and the throttle setting will have to be modified whenever the rotor power demand changes so that the speed does not change. Chapter 6 considers engines and power control.

There are two main forces acting on a helicopter, the force due to gravity, which is always downwards, and the rotor thrust vector, which is always at right angles to the tip path plane, otherwise called the rotor disc. Chapter 2 explains how the result of forces acting in various ways can be predicted and Chapter 3 shows how rotors develop thrust. The pilot can control the magnitude of the rotor thrust with the collective pitch lever held in his left hand, and the direction of the rotor thrust with the cyclic stick held in his right hand. The cyclic stick works in two dimensions: if the stick is pushed in any direction, the rotor thrust tilts the same way. These two fundamental controls are illustrated in Figure 1.21.

The blade movements necessary to produce lift and to achieve control will be outlined in Chapter 3, whereas Chapter 4 treats the construction and dynamics of the blades

Fig. 1.21 The fundamental rotor controls. The cyclic stick tilts the rotor in the direction it is moved, whereas the collective lever changes the magnitude of the thrust.

and rotor head. Chapter 7 integrates the control system and considers power assistance and auto-stabilization.

The pilot controls the yaw axis by altering the pitch of the tail rotor blades using foot pedals. Chapter 5 considers the tail system of the helicopter.

It should be mentioned in passing that the No. 1 pilot in a helicopter conventionally occupies the right hand seat; the opposite of aeroplane practice. In some early machines, only one collective lever was provided, between the seats. The test pilots would sit in the left seat, as per aeroplane practice. Because of the difficulty of reversing the function of left and right hands, a pilot under training would be placed in the right seat and so the right seat became the conventional location for a helicopter pilot. A further factor is that in early helicopters, the forces fed back to the cyclic stick from the rotor were such that it was not safe to let go of the stick for an instant. However, the collective lever could be released temporarily. Given that most secondary controls such as the radio and instruments are centrally disposed so that pilot and co-pilot can both see them, it made sense to put the pilot in command on the right where his free left hand would be of most use.

The power systems of a typical helicopter are not that much different from those of any aircraft. Electrical power is needed for instruments, radios, autopilots, lighting, engine starting, navigation and intercom systems, as well as a host of further avionics that might be needed for special purposes.

A light helicopter may have no power assistance, but as machines get larger the control forces may cause fatigue and in very large machines they will be beyond the strength of the pilot. Power-assisted controls then become essential. Power controls are also needed if some kind of automatic stabilization or autopilot is fitted so that the low powered electronic signals can operate the controls.

When powered controls operated by electrical signals have faultless reliability, the mechanical controls from the pilot can also be replaced by electrical controls, leading to the concept of fly-by-wire. The pilot operates controls having no mechanical connection to the rotors, but which instead produce electrical signals. This concept is explored in Chapter 7.

Electric motors are useful for low powered control purposes such as the trim mecha­nism, but hydraulics allows greater forces to be developed within small actuators, and so they will be used for powered flying controls.

Electrical and hydraulic power is vital to the safety of the machine, and the hydraulic pump and the generator may be driven from the rotor shaft so that power is still available even in the case of engine failure. In small machines the generator is driven from the engine, as battery capacity is enough to keep the electrical system working in the case of an engine failure. Larger machines may have two or more engines and each will have a generator so that electric power is still available in case of engine failure.

The electrical system is discussed in Chapter 6, and an explanation of hydraulic controls will be found in Chapter 7.

Many of the instruments fitted to helicopters are the same as those used in other aircraft, but in addition to the usual engine-related gauges the helicopter will also need

a rotor tachometer. The response of a helicopter to control inputs depends on rotor speed, and this needs to be controlled to close limits. The rotor tachometer and engine- related instruments are detailed in Chapter 6, whereas flight instruments are covered in Chapter 7.

References

1 Spenser, J. P., Whirlybirds, University of Washington Press, Seattle, ISBN 0-295-97699-3 (1998)

2 Spenser, IP., Vertical Challenge, University of Washington Press, Seattle, ISBN 0-295-97203-3

(1998)

3 Coates, S., Helicopters of the ThirdReich, Classic Publications, Hersham, ISBN 1-903223-24-5 (2002)

4 Boulet, J., LHistoire de l’Helicoptere, Editions France-Empire, Paris, ISBN 2-7048-0040-5 (1982)

5 DuMoulin, A., Les Helicopteres Florine 1920-1950, Fonds National Alfred Renard, Brussels

(1999)

6 Everett-Heath, J., British Military Helicopters, Arms and Armour Press, London, ISBN 0-85368-805-2(1986)

7 Nowarra, H. J., German Helicopters, Schiffer, West Chester, ISBN 0-88740-289-5 (1990)

8 Dowling, J., RAF Helicopters: the first twenty years, HmSo, London, ISBN 0-11-772725-3 (1992)

Acknowledgements Posted by admin in The Art of the Helicopter on February 27, 2016 The author is indebted to the many people and organizations who have found time to help in the preparation of this book by offering information, photographs, constructive criticism or simply encouragement. High on the list must come my publishers, Elsevier. Ray Prouty’s columns in Rotor and Wing have long been an inspiration that complex subjects can be brought to a wide audience. Much material was obtained from the International Helicopter Museum in Weston- super-Mare, UK, The Fleet Air Arm Museum in Yeovilton, UK, The Museum of Flight in Seattle, Washington, The Igor I. Sikorsky Historical Archives in Stratford, Connecticut, The Hiller Aviation Museum in San Carlos, California and the American Helicopter Museum and Education Center in Brandywine, Pennsylvania. The kindness and helpfulness of the staff of all of these was exceptional and deeply appreciated. The universally positive attitude of the manufacturers has been a great delight. AgustaWestland, Bell Helicopter Textron, Boeing Helicopter, Kaman Aerospace, Lockheed Martin and Sikorsky must all be mentioned here. Reg Austin did a superb job of checking my words for technical accuracy. Mikael Reichel advised on the pedagogical aspects of the text and many of my explanations are the better for that. I would not have obtained all of the necessary photographs and permissions without the assistance of Liza Marshall. I am indebted to Steve Coates for allowing me access to his collection of wartime German helicopter material. Individuals who have helped include Fred Ballam, Oliver Dearden, Margaret Denley, George Done, David Gibbings, Nick Gribble, Bruce Holben, Russell H. Jones, Bill Kidd, Dan Libertino, Bo Maggs, Tim Price, Renee Renaud, Trevor Scantlebury, Eric Schulzinger, Tom Shenton, Jonathan Simpson, Jay P. Spenser, David Steel, North E. West and Katharine Williams. The Art of the Helicopter Posted by admin in The Art of the Helicopter on February 26, 2016 The modern helicopter is a sophisticated device that merges a surprising number of technologies together. This wide range of disciplines is one of the fascinations of the heli­copter, but it also makes a complete understanding difficult. The very ability to hover, which sets the helicopter apart, also dooms it forever to vibration, poor performance and economy in forward flight, and thus restricts its numbers. The unique capabilities, complexity and inherent limitations are part of a helicopter’s charm, and have given rise to some wonderful definitions and descriptions, which generally contain more than a grain of truth: A helicopter is a mechanical engineer’s dream and an aerodynamicist’s nightmare. A helicopter is a collection of ball-races flying in close formation. A helicopter is a collection of vibrations held together by differential equations. My own search for an understanding of the helicopter was hampered by the huge gap between books containing beautiful photographs but little information and advanced textbooks full of equations. This, then, is the book that I couldn’t buy when I wanted to learn all this; it could not be a conventional book because I have had such difficulty with them. It combines theory and practice of how helicopters are made, how they fly, how they are powered and how they are controlled. It would be impossible to consider all of that without at least some reference to flying techniques. Most technical books assume an existing level of knowledge, but the wide readership and wide range of disciplines make that inappropriate here. Instead of making incorrect assumptions about the reader, this book approaches every subject from first principles, and builds up in a clearly explained logical sequence using plain English and clear diagrams, avoiding unnecessary mathematics. Technical terms and buzzwords are all defined, and acronyms are spelled out. Misnomers, myths and old wives’ tales (for these are plentiful) are disposed of wherever they arise. Whilst the contents of this book are expressed in straightforward language there is no oversimplification and all of the content is based on established physics and accepted theory. The student of technology or aerodynamics will find here a concise introduction, leading naturally to the more advanced textbooks on the subject. The would-be pilot will find clear explanations of the principles to act as a per­fect complement to the instruction itself. The experienced pilot will find the detailed descriptions of the characteristics of helicopters an aid to safety. This book covers the theory of the helicopter in more than sufficient depth to enable the reader to pass the helicopter theory examination. There is enough practical information to allow the reader to make sense of the machine’s flight manual and to prepare for the helicopter type examination. The rotary wing flying machine is just part of the larger subject of general aviation. Related subjects such as human factors, meteorology, air law and navigation scarcely differ with the type of flying machine, and are not repeated here save for differences specific to helicopters. John Watkinson Burghfield Common, England « Previous 1 2 Tweet Copyright © 2024 Helicopters & Aircrafts - Everything about aircrafts and helicopters. News and events in aviation worldwide. Civil, transportation, military helicopters and airplanes.