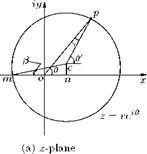
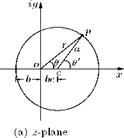
For transforming a circle to a cambered aerofoil, using Joukowski transformation, the center of the circle in the physical plane has to be shifted to a point in one of the quadrants. Let us consider the center in the first coordinate of z-plane, as shown in Figure 4.8(a).

|
Figure 4.8 Transformation of a circle to a cambered aerofoil.
|
|
As seen in Figure 4.8(a):
• the center c of the circle is displaced horizontally as well as vertically from the origin, in the physical plane.
• let the horizontal shift of the center be “on = be" and
• the vertical shift be “cn = h"
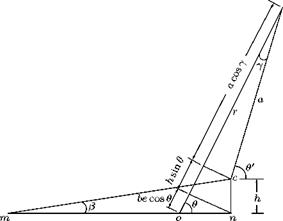
The point p on the circle and its distance from the origin can be represented as shown in Figure 4.9.
Both the vertical shift h and eccentricity e are small. Therefore, the angle в, subtended at point m, by om and cm is small, hence, cos в & 1, also cos у & 1. Therefore, the radius of the circle becomes:
a = (b + be) cos в = (b + be).
The vertical shift of the center can be expressed as:
h = a sin в = b (1 + е)в.
But e and в are small, therefore, h becomes:
h ^ Ьв
By dropping perpendiculars on to op, from n and c, it can be shown that: op = r = a cos у + h sin в + be cos в.
The angle y is small, therefore, cos y ^ 1, thus:
r = a + h sin в + be cos в. Substituting for a = (b + be) and h = Ьв, r becomes:
r = b + be + bв sin в + be cos в.
This can be expressed as:
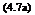 r
r
– = 1 + e + e cos в + в sin в b
or
– = [1 + (e + e cos в + в sin в)]
Expanding and retaining only the first order terms, we have:
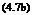 – = 1 — e — e cos в — в sin в r
– = 1 — e — e cos в — в sin в r
since e and в are small, their powers are assumed to be negligibly small. The Joukowski transformation function is:
b2
Z = Z + —.
z
Replacing z with r е’в, we have:
reie + – e-ie
r
rb
Substituting for — and – from Equations (4.7a) and (4.7b), we get: br
Z = 2b cos в + i2b(e + e cos в + в sin в) sin в
or
Z + in = 2b cos в + i2b(e + e cos в + в sin в) sin в.
Equating the real and imaginary parts, we get:
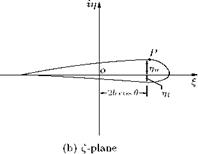
These coordinates represent a cambered aerofoil, in the Z-plane, as shown in Figure 4.8(b). Thus, the circle with center c in the first quadrant of z-plane is transformed to a cambered aerofoil section in the Z-plane, as shown in Figure 4.8(b), with coordinates Z and n, given by Equations (4.8a) and (4.8b). It is seen that:
• The chord of the cambered aerofoil is also 4b, as in the case of symmetrical aerofoil.
• When в = 0, that is, when there is no vertical shift for the center of the circle, in the physical plane, the transformation results in a symmetrical aerofoil in the transformed or Z-plane.
• The second term in the n expression, in Equation (4.8b), alters the shape of the aerofoil section, because it is always a positive addition to the n-coordinate (ordinate).
• The trailing edge is sharp (n = 0, at в = n), and the fmax is at the quarter chord point (Z = b).
![]() Camber = 2 (Пи + Пі)
Camber = 2 (Пи + Пі)![]() 4b в (sin 9)max
4b в (sin 9)max










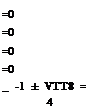 d(t/c)/dB e(cos ви + cos2 ви – sin2 ви) cos ви + cos2 ви – (1 – cos2 ви)
d(t/c)/dB e(cos ви + cos2 ви – sin2 ви) cos ви + cos2 ви – (1 – cos2 ви)


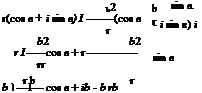
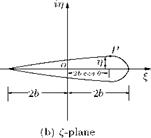

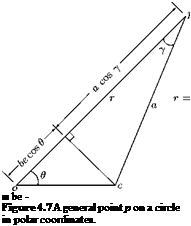 the radius of the circle is (b + be). Let us represent the general point p on the circle, in polar coordinates, as shown in Figure 4.7.
the radius of the circle is (b + be). Let us represent the general point p on the circle, in polar coordinates, as shown in Figure 4.7.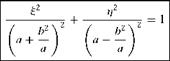 (4.3)
(4.3)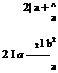 The fineness ratio of the ellipse, defined as the ratio of the chord to maximum thickness, becomes:
The fineness ratio of the ellipse, defined as the ratio of the chord to maximum thickness, becomes:
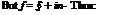

 iy■
iy■