Solutions of Viscous Flows: A. Preliminary Discussion
The governing continuity, momentum, and energy equations for a general unsteady, compressible, viscous, three-dimensional flow are given by Equations (2.52), (15.19a to c), and (15.26), respectively. Examine these equations closely. They are nonlinear, coupled, partial differential equations. Moreover, they have additional terms— namely, the viscous terms—in comparison to the analogous equations for an inviscid flow treated in Part 3. Since we have already seen that the nonlinear inviscid flow equations do not lend themselves to a general analytical solution, we can certainly expect the viscous flow equations also not to have any general solutions (at least, at the time of this writing, no general analytical solutions have been found). This leads to the following question: How, then, can we make use of the viscous flow equations in order to obtain some practical results? The answer is much like our approach to the solution of inviscid flows. We have the following options:
1. There are a few viscous flow problems which, by their physical and geometrical nature, allow many terms in the Navier-Stokes solutions to be precisely zero, with the resulting equations being simple enough to solve, either analytically or by simple numerical methods. Sometimes this class of solutions is called “exact solutions” of the Navier-Stokes equations, because no simplifying approximations are made to reduce the equations—just precise conditions are applied to reduce the equations. Chapter 16 is devoted to this class of solutions; examples are Couette flow and Poiseuille flow (to be defined later).
2. We can simplify the equations by treating certain classes of physical problems for which some terms in the viscous flow equations are small and can be neglected. This is an approximation, not a precise condition. The boundary-layer equations developed and discussed in Chapter 17 are a case in point. However, as we will see, the boundary-layer equations may be simpler than the full viscous flow equations, but they are still nonlinear.
3. We can tackle the solution of the full viscous flow equations by modem numerical techniques. For example, some of the computational fluid dynamic algorithms discussed in Chapter 13 in conjunction with “exact” solutions for the inviscid flow equations carry over to exact solutions for the viscous flow equations. These matters will be discussed in Chapter 20.
There are some inherent very important differences between the analysis of viscous flows and the study of inviscid flows that were presented in Parts 2 and 3. The remainder of this section highlights these differences.
First, we have already demonstrated in Example 2.4 that viscous flows are rotational flows. Therefore, a velocity potential cannot be defined for a viscous flow, thus losing the attendant advantages that were discussed in Sections 2.15 and 11.2. On the other hand, a stream function can be defined, because the stream function satisfies the continuity equation and has nothing to do with the flow being rotational or irrotational (see Section 2.14).
Second, the boundary condition at a solid surface for a viscous flow is the noslip condition. Due to the presence of friction between the surface material and the adjacent layer of fluid, the fluid velocity right at the surface is zero. This no-slip condition was discussed in Section 15.2. For example, if the surface is located at у = 0 in a cartesian coordinate system, then the no-slip boundary condition on velocity is
At у = 0; и = 0 u = 0 w = 0
This is in contrast to the analogous boundary condition for an inviscid flow, namely, the flow-tangency condition at a surface as discussed in Section 3.7, where only the component of the velocity normal to the surface is zero. Also, recall that for an inviscid flow, there is no boundary condition on the temperature; the temperature of the gas adjacent to a solid surface in an inviscid flow is governed by the physics of the flow field and has no connection whatsoever with the actual wall temperature. However, for a viscous flow, the mechanism of thermal conduction ensures that the temperature of the fluid immediately adjacent to the surface is the same as the temperature of
the material surface. In this respect, the no-slip condition is more general than that applied to the velocity; in addition to и = v = 0 at the wall, we also have T = Tw at the wall, where T is the gas temperature immediately adjacent to the wall and Tw is the temperature of the surface material. Thus,
Aty= 0: T = TW [15.34]
Tn many problems, Tw is specified and held constant; this boundary condition is easily applied. However, consider the following, more general case. Imagine a viscous flow over a surface where heat is being transferred from the gas to the surface, or vice versa. Also, assume that the surface is at a certain temperature, Tw, when the flow first starts, but that Tw changes as a function of time as the surface is either heated or cooled by the flow [i. e., Tw = Tw(t)]. Because this timewise variation is dictated in part by the flow which is being calculated, Tw becomes an unknown in the problem and must be calculated along with the solution of the viscous flow. For this general case, the boundary condition at the surface is obtained from Equation (15.2) applied at the wall; that is,
Aty= 0: qw = -(kd-^j [15.35]
Here, the surface material is responding to the heat transfer to the wall qw, hence changing Tw, which in turn affects qw. This general, unsteady heat transfer problem must be solved by treating the viscous flow and the thermal response of the material simultaneously. This problem is beyond the scope of the present book.
Finally, let us imagine the above, unsteady case carried out to the limit of large times. That is, imagine a wind-tunnel model which is at room temperature suddenly inserted in a supersonic or hypersonic stream. At early times, say, for the first few seconds, the surface temperature remains relatively cool, and the assumption of constant wall temperature Tw is reasonable [Equation (15.34)]. However, due to the heat transfer to the model [Equation (15.35)], the surface temperature soon starts to increase and becomes a function of time, as discussed in the previous paragraph. However, as Tw increases, the heating rate decreases. Finally, at large times, Tw increases to a high enough value that the net heat transfer rate to the surface becomes zero, that is, from Equation (15.35),
q<u
or (— =0 [15.36]
Ь К
When the situation of zero heat transfer is achieved, a state of equilibrium exists; the wall temperature at which this occurs is, by definition, the equilibrium wall temperature, or, as it is more commonly denoted, the adiabatic wall temperature, Taw. Hence, for the case of an adiabatic wall (no heat transfer), the wall boundary condition is given by Equation (15.36).
In summary, for the wall boundary condition associated with the solution of the energy equation [Equation (15.26)], we have three possible cases:
1. Constant temperature wall, where Tw is a specified constant [Equation (15.34)]. For this given wall temperature, the temperature gradient at the wall (dT/dy)w is obtained as part of the flow-field solution and allows the direct calculation of the aerodynamic heating to the wall via Equation (15.35).
2. The general, unsteady case, where the heat transfer to the wall qw causes the wall temperature Tw to change, which in turn causes qw to change. Here, both Tw and (ЗT/3 v )„ change as a function of time, and the problem must be solved by treating jointly the viscous flow as well as the thermal response of the wall material (which usually implies a separate thermal conduction heat transfer numerical analysis).
3. The adiabatic wall case (zero heat transfer), where (дТ/dy)w = 0 [Equation)^.36)]. Here, the boundary condition is applied to the temperature gradient at the wall, not to the wall temperature itself. Indeed, the wall temperature for this case is defined as the adiabatic wall temperature Taw and is obtained as part of the flow-field solution.
Finally, we emphasize again that, from the point of view of applied aerodynamics, the practical results obtained from a viscous flow analysis are the skin friction and heat transfer at the surface. However, to obtain these quantities, we usually need a complete solution of the viscous flow field; among the data obtained from such a solution are the velocity and temperature gradients at the wall. These, in turn, allow the direct calculation of rw and qw from
and
Another practical result provided by a viscous flow analysis is the prediction and calculation of flow separation; we have discussed numerous cases in the preceding chapters where the pressure field around an aerodynamic body can be greatly changed by flow separation; the flows over cylinders and spheres (see Sections 3.18 and 6.6) are cases in point.
Clearly, the study of viscous flow is important within the entire scope of aerodynamics. The purpose of the following chapters is to provide an introduction to such flows. We will organize our study following the three options itemized at the beginning of this section; that is, we will treat, in turn, certain specialized “exact” solutions of the Navier-Stokes equations, boundary-layer solutions, and then “exact” numerical solutions of Navier-Stokes equations. In so doing, we hope that the reader will gain an overall, introductory picture of the whole area of viscous flow. Entire books have been written on this subject, see, for example, References 42 and 43. We cannot possibly present such detail here; rather, our objective is simply to provide a “feel” for and a basic understanding of the material. Let us proceed.
Problems
1. Consider the incompressible viscous flow of air between two infinitely long parallel plates separated by a distance h. The bottom plate is stationary, and the top plate is moving at the constant velocity ue in the direction of the plate. Assume that no pressure gradient exists in the flow direction.
(a) Obtain an expression for the variation of velocity between the plates.
(b) If T = constant = 320 K, ue = 30 m/s, and h = 0.01 m, calculate the shear stress on the top and bottom plates.
2. Assume that the two parallel plates in Problem 15.1 are both stationary but that a constant pressure gradient exists in the flow direction (i. e., dp/dx = constant).
(a) Obtain an expression for the variation of velocity between the plates.
(b) Obtain an expression for the shear stress on the plates in terms of dp/dx.











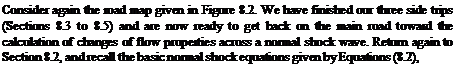
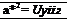 [8.55]
[8.55]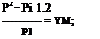
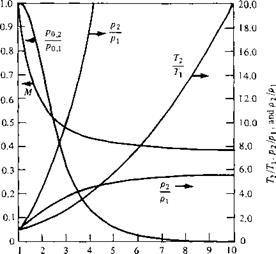
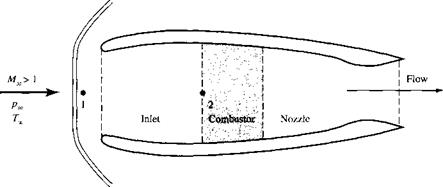
 Imaginary state 1 a where the fluid element has been brought to rest isentropically. Thus, in state la, the pressure is p0,i (by definition). Entropy is still Si. Temperature is Tq і (by definition).
Imaginary state 1 a where the fluid element has been brought to rest isentropically. Thus, in state la, the pressure is p0,i (by definition). Entropy is still Si. Temperature is Tq і (by definition).