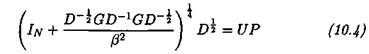1. INTRODUCTION
The previous chapters emphasized the usefulness and efficiency of the H analysis techniques. Nevertheless, as remarked in chapter 7 (section
3. ), the application of these techniques is unreliable in specific fields, such as the control of flexible structures.
Remember indeed that the principle of ц analysis is to compute the s. s.v. as a function of frequency^: the robustness margin is then
deduced as the inverse of the maximal s. s.v. over the frequency range. In practice, the s. s.v. ш)) is usually computed at each point of a frequency gridding. This technique is however unreliable in the case of narrow and high peaks on the ц plot, since it becomes possible to miss the critical frequency (i. e. the frequency for which the maximal s. s.v. is obtained may lie between two points of the gridding), and thus to overevaluate the robustness margin. This problem especially arises in the case of flexible systems (Freudenberg and Morton, 1992). As a consequence, there has been a regain of interest for robustness analysis techniques, which do not use a frequency gridding: see e. g. (Ly et al., 1994).
The solution proposed in chapter 7 (section 3.) consists in transforming a classical frequency dependent ц analysis problem into an augmented skewed n problem, in which the frequency и appears as an additional uncertainty (namely a real repeated scalar). It becomes then possible to directly compute the maximal s. s.v. over a frequency interval [u>, £3]. Two problems however arise:
■ Because of the NP hard characteristics of the fi problem, an upper bound is computed instead of the exact value of /і. In order to reduce the conservatism of this upper bound, which is calculated for the
augmented pi problem, it is more interesting to consider a set of small intervals [wj, ші+i] instead of a large frequency interval [u>, Щ.
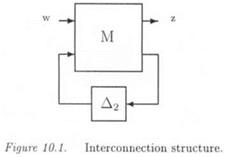
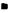 The size of the augmented pi problem (which is to compute the maximal s. s.v. pi(u) over an interval [и,, Wj+i]) can be much larger than the size of the original problem (the computation of the s. s.v. , (g ) at a fixed frequency a»). With reference to subsection 2.3 of chapter 5, remember that the problem of computing the pi upper bound of (Fan et al., 1991) reduces to an LMI problem, in which the optimization parameters are scaling matrices D and G. The computation of the optimal D, G scaling matrices for the augmented pi problem can be a computationally (very) involving task: more precisely, with reference to Lemma 3..1 of chapter 7, the model perturbation corresponding to the augmented pi problem contains the initial model uncertainties and the frequency. The associated D, G scaling matrices can thus be split into the D,G scaling matrices, corresponding to the uncertain frequency, and the D2 , D2 scaling matrices corresponding to the initial model uncertainties. The computational burden of the augmented pi problem is often very heavy, because the D,, G, scaling matrices contain numerous optimization parameters of the LMI problem: the uncertain frequency appears indeed as a repeated real scalar Su)Im, where m denotes the order of the state-space model of M(s) in the standard interconnection structure M(s) – Д.
The size of the augmented pi problem (which is to compute the maximal s. s.v. pi(u) over an interval [и,, Wj+i]) can be much larger than the size of the original problem (the computation of the s. s.v. , (g ) at a fixed frequency a»). With reference to subsection 2.3 of chapter 5, remember that the problem of computing the pi upper bound of (Fan et al., 1991) reduces to an LMI problem, in which the optimization parameters are scaling matrices D and G. The computation of the optimal D, G scaling matrices for the augmented pi problem can be a computationally (very) involving task: more precisely, with reference to Lemma 3..1 of chapter 7, the model perturbation corresponding to the augmented pi problem contains the initial model uncertainties and the frequency. The associated D, G scaling matrices can thus be split into the D,G scaling matrices, corresponding to the uncertain frequency, and the D2 , D2 scaling matrices corresponding to the initial model uncertainties. The computational burden of the augmented pi problem is often very heavy, because the D,, G, scaling matrices contain numerous optimization parameters of the LMI problem: the uncertain frequency appears indeed as a repeated real scalar Su)Im, where m denotes the order of the state-space model of M(s) in the standard interconnection structure M(s) – Д.
An alternative solution was proposed in e. g. (Feron, 1997; Gahinet et al., 1995). The idea is to synthesize D, G scaling matrices, which simultaneously work at two neighboring frequencies wi and u>2- Since this method does not use the augmented pi problem above, the computational burden is expected to be much lower. Moreover, this heuristic technique can be theoretically justified: it is proved indeed that when the frequencies ш and D2 are sufficiently close (in a sense which will be precisely defined in the following), the D, G scaling matrices work on the whole segment, defined by its two extremal frequencies ш and a>2.
Even when the frequencies u>i and G2 are not a priori sufficiently close, D, G scaling matrices can be synthesized, which simultaneously work at these two frequencies, and it is checked a posteriori whether the D, G scaling matrices work indeed on the whole segment. This chapter especially proposes an easy and yet rigorous method, for solving this last problem of checking the validity of D, G scaling matrices on the whole segment. This method essentially relies on the alternative formulation of the mixed pt upper bound of (Fan et al., 1991), which was proposed in (Young et al., 1995).
The technique is finally applied to the flexible airplane problem (Fer-
reres and Biannic, 1998b) and to the telescope mock-up (Ferreres et al., 1998). See also (Magni et al., 1999) for an alternative technique, which is complementary to the one proposed here. The chapter is organized as follows. The relationship between both formulations of the mixed p, upper bound of (Fan et al., 1991; Young et al., 1995) is clarified in the second section. The basis of the method is presented in sections 3 and
4. The algorithm is summarized in section 5. The application is finally done in section 6.











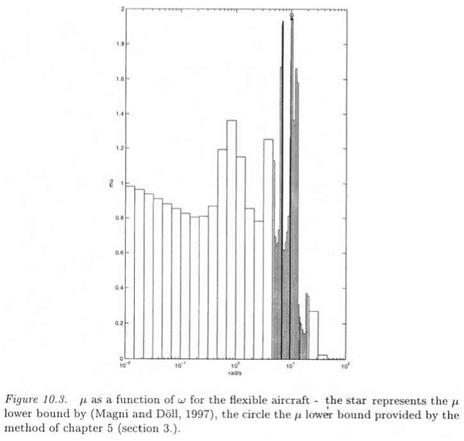

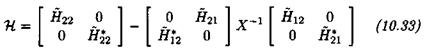

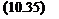 _ 1
_ 1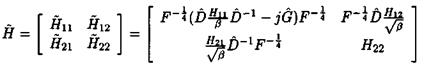
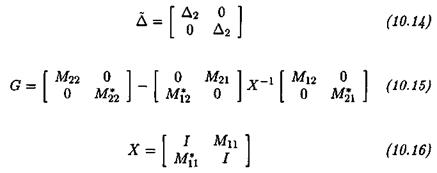
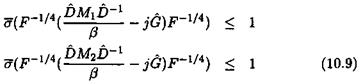

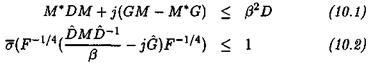
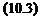 D = P
D = P