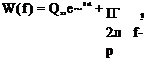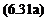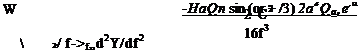Airfoil With Finite Trailing-Edge Angle
The Joukowski airfoils have cusped trailing edges as has been seen for the flat plate, circular arc, and symmetric examples. The cusped trailing edge presents some numerical difficulties for panel-method solutions since in the neighborhood of the trailing edge the airfoil’s upper and lower surfaces coincide. Therefore, for the purpose of providing exact solutions to test the results of the panel methods to be
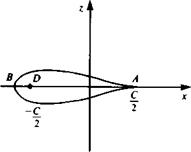
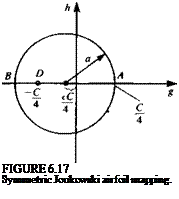
Symmetric Joukowski Airfoil
For an airfoil of chord c and thickness parameter є the radius of the circle in the /plane is a (Fig. 6.17) where
|
c’=1- fl*. |
![]()
![]()

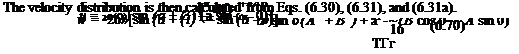 |
a = ^(l + e)
where the airfoil chord c is
с = ^(з + 2е+ 1 )
4 1 + 2є/
The x, z coordinates of the airfoil are given in Eq. (6.57) as
C2
/ fC , 16
x = a cos 0 ——I 1 H————— —;———-
V 4 / / єС2 .
^a cos 0 – — j + a cos
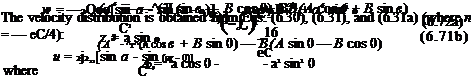 |
В = 2a sin 0( a cos 0 ——
and the pressure coefficient is calculated by using Eq. (6.70).
The Van de Vooren Airfoil
|
a2k (1 + є)*’1 |
The parameters for this airfoil are shown in Fig. 6.18 where the chord length is 21 and is given from Eq. (6.65) as
Here є is the thickness parameter and к is the trailing-edge angle parameter (see Eq. (6.66)) and a is the radius of the circle in the / plane.
The x, z coordinates of the Van de Vooren airfoil are then given in Eq. (6.63) as
rk
x = -£гт [cos k6x cos (к — 1)02 + sin квх sin (к — 1)02] (6.74a)
r2
rk
z = [sin квх cos (к — 1 )02 – cos k6x sin (к – 1 )02] (6.746)
f"i = V(a cos в — a)2 + a2 sin5 0
r2 = V(a cos 0 – єа)2 + a2 sin2 0
„ a sin 0
0i = tan —————- v я
a cos 0 — a
Here Пі depends on the quadrant where 02 is being evaluated (has a value of 0 in the first quadrant, 1 in the second and third quadrants and 2 in the fourth quadrant).
|
r* sin a – sin (a — 0) |
|
w = -2 <2* |
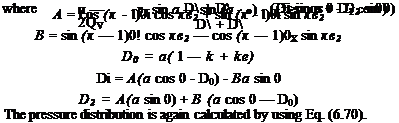 |
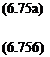 |
The velocity distribution is then given from the solution in the circle plane plus the transformation (Eq. (6.62)) as











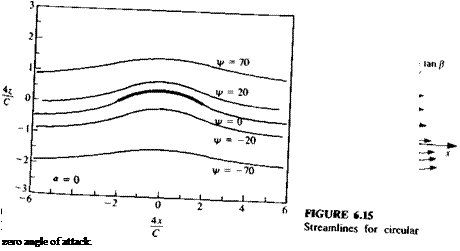
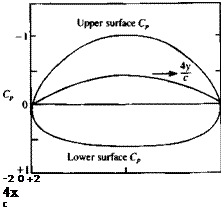 Pressure coefficient for circular arc at zero angle of attack.
Pressure coefficient for circular arc at zero angle of attack. (6.47)
(6.47)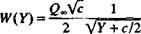 (6.51)
(6.51)
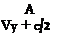
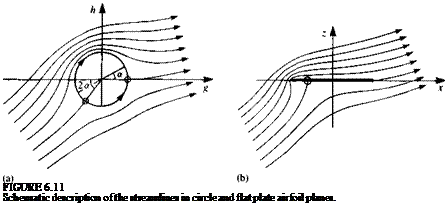
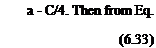 Choose the circle with its center at the origin and (6-27),
Choose the circle with its center at the origin and (6-27),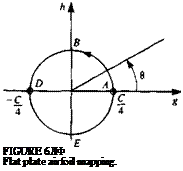
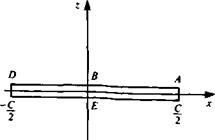
![Flat Plate Airfoil Подпись: [sin a — sin (a — 0)] sin 0](/img/3130/image576_2.gif)