Flow in a supersonic wind-tunnel
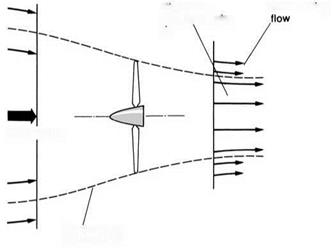
The fact that radically different flows occur at sub – and supersonic speeds with objects having identical geometric features is also graphically illustrated by the flow in a duct of the type which is used in supersonic wind-tunnels (Fig. 5.4).
If the tunnel is run subsonically then, as would be expected from Chapter 1 the speed of flow increases until the narrowest portion (the throat) is reached and decreases again as the duct area increases. If, however, the tunnel is running supersonically, the speed continues to increase downstream of the throat, even though the cross-sectional area is getting larger.
At first sight it may seem that this is impossible because the same mass flow must pass each section in unit time. Thus it would appear that a lower speed of flow will be needed at a point in the duct where the cross-sectional area is high, and vice versa.
The solution to this dilemma lies in the fact that the density of the air reduces as the speed is increased. At low speed this effect is not very significant, but as the speed increases the effect becomes so pronounced that an increase in duct area is required to pass the mass flow in spite of the fact that the speed is also increasing (Fig. 5.4).
This change of density starts to become noticeable some time before the flow actually becomes supersonic in that pressures predicted by the Bernoulli equation (Chapter 1) become progressively less accurate. Thus one way of distinguishing between high and low speed flows is to ask the question whether the density changes within the flow are significant or not. For this reason flow at high speed is sometimes referred to as compressible flow. This distinction is valid for ‘external’ flows, such as the flow round the aerofoil discussed above, as well as ‘internal’ flows such as the supersonic wind-tunnel duct.













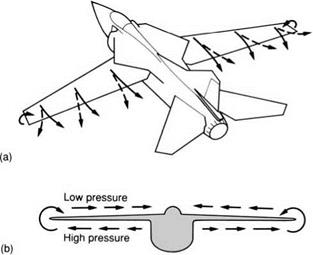
 Relative flow
Relative flow
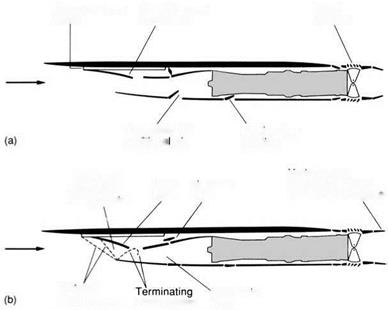 Boundary layer Movable ramp
Boundary layer Movable ramp